DOI: 10.11817/j.issn.1672-7207.2016.02.044
基于经验模式分解和自适应神经模糊推理的风速短期智能预测混合方法
刘辉1, 2,张雷1,田红旗1,梁习锋 1,李燕飞1
(1. 中南大学 交通运输工程学院,轨道交通安全教育部重点实验室,湖南 长沙,410075;
2. 德国Rostock大学 信息与电子工程学院,德国 罗斯托克,18109)
摘要:为实现风速的超前多步高精度预测,提出一种基于经验模式分解与自适应神经模糊推理的混合方法。该方法利用经验模式分解法对铁路风速进行多层分解计算以降低风速的强随机性,对分解后的各层风速数据分别建立自适应神经模糊推理预测模型并完成预测计算,最终加权各层预测值获得原实测数据的对应步数的预测结果。运用所提出的方法对青藏铁路某监控点的风速进行预测。研究结果表明:所提出的混合方法有效融合了经验模式分解法的信号细分性能和自适应神经模糊推理法的非线性追踪能力,混合模型的超前1步、2步、3步预测的平均相对误差分别为6.24%,11.11%和14.30%,体现出良好的非平稳信号预测性能。
关键词:铁路安全;风速预测;经验模式分解;自适应模糊推理
中图分类号:U216 文献标志码:A 文章编号:1672-7207(2016)02-0676-07
Short-term wind speed intelligent prediction method based on empirical mode decomposition and adaptive neural fuzzy inference system
LIU Hui1, 2, ZHANG Lei1, TIAN Hongqi1, LIANG Xifeng1, LI Yanfei1
(1. Key Laboratory of Traffic Safety on Track of Ministry of Education,
School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China;
2. Institute of Automation, Faculty of Informatics and Electrical Engineering,
University of Rostock, Rostock 18109, Germany)
Abstract: To get high-precision forecasting results, a hybrid method was proposed by adopting the empirical mode decomposition and the adaptive neural fuzzy inference system. The procedures of the proposed method are as follows. Firstly, use the empirical mode decomposition to decompose the non-stationary wind speed series into a group of sub wind speed layers. Secondly, utilize the adaptive neural fuzzy inference system to build multi-step forecasting models for all the decomposed wind speed layers. Thirdly, sum up the multi-step forecasting results of the decomposed layers to get the final predictions for the original wind speed signals. Experiment was made using the wind speed data sampled from a monitoring wind station along the Qinghai—Tibet railway. The results show that the proposed method combines the decomposing performance of the empirical mode decomposition and the nonlinear performance of the adaptive neural fuzzy inference system effectively. The mean percentage errors of the one-three step ahead forecasting results are 6.24%, 11.11% and 14.30%,respectively.Those errors indicate that the proposed method has satisfactory forecasting performance.
Key words: railway security; wind speed forecast; empirical mode decomposition; adaptive neural fuzzy inference system
在铁路与轨道交通领域,强风是造成行车事故的主要自然灾害之一[1]。到目前为止,中国、日本、加拿大等国均发生过铁路强风灾害[2]。随着高速列车在世界范围内的推广和普及,尤其在列车行车速度越来越快的情况下,如何保障强风环境下的列车行车安全显得格外重要。为了降低强风对铁路运营所造成的危害,国内外铁路研究机构在铁路挡风墙[3-5]、列车气动外形优化[6-7]、强风列车倾覆稳定性建模[1, 8-9]、耦合数值计算[10-13]等方面开展研究并取得了重要进展。近年来,包括我国在内的世界铁路发展大国开始特别关注于研建一种基于风环境/列车/线路耦合决策的新型铁路强风实时监控与预警系统,如德国国家铁路公司(Deutsche Bahn AG)所研建的Nowcasting System大风监测预警系统[14]、日本铁路公司(JR-EAST)所设计的Windas system大风列车预警系统[15]、我国原铁道部委托中南大学等单位自主设计的大风预警系统[16]。这些铁路预警系统通过测量铁路沿线的风速,融合线路上的实时行车信息,计算不同风速阈值下的列车临界安全速度,实现大风下的列车预警和指挥[14-16]。虽然这类第一代预警系统已经开始逐步投入使用并发挥作用,但尚未解决风速预测的难题,目前这些预警系统都采用测风站的实测风速来计算临界安全速度阈值。这种基于实测风速的模式虽也能用于指挥行车,但当强风现象消失后,铁路调度部门由于无法预知其未来风速趋势,为了保障列车的行车安全,采取让列车继续保持一段时间的“低速运行”或“停车”措施。这降低了行车效率[14-16]。反之,调度部门若能提前掌握沿线监控区域的风速短期预测趋势,则可以根据预测风速做出“保持限速”、“保持停轮”或“解除预警”等决定。此外,实际上只有实现了高精度的铁路沿线风速超前多步预测,当面对突发强风风速时,运行列车才有应急处理的时间来完成减速或停轮等操作。风速短期预测已成为世界各国争先解决的关键问题,也成为研建第二代预警系统的瓶颈技术。与其他工程领域的风速预测不同,铁路风速预测侧重于对风速信号在未来几秒钟到几分钟内的“短期”计算,强调预测输出的“实时性”和对瞬间跳跃风速点的“精确追踪”。HOPPMANN等[14]提出了一种利用统计原理实现预测的策略。通过对铁路沿线的海量历史风速进行数理统计,找到潜在数学规律从而实现对风速的递推预测。虽然统计方法具有简单、实时性能好等优点,但也存在预测精度不高的缺陷。KOBAYASHI等[15]提出了基于卡尔曼滤波理论的铁路风速预测方法。该方法尝试运用智能优化理论来解决铁路非平稳风速的预测问题。其所建立的卡尔曼预测模型虽然能够较高精度地拟合铁路沿线风速的变化规律,但也没有解决根据实测风速建立高精度卡尔曼状态和测量方程的技术难题,使得所提出的卡尔曼预测器无法在实际预警系统中直接使用。刘辉等[2, 17]提出了时间序列和BP神经网络的铁路风速短期预测模型,有效地解决了风速的中等精度预测难题。本文作者认为铁路风速作为一类极具突变性和非线性的随机信号,要实现更高精度的超前多步短期预测,必须从2个方面同时开展研究:1) 如何在尽可能多地保留风速信号成分的前提下进一步降低原始风速数据的突变性和非线性;2) 如何找到一种能够有效追踪风速突变性和非线性的智能学习模型来实现对风速的更高精度超前多步预测计算。考虑上述2个因素,本文作者以我国典型的强风高原铁路—青藏铁路的某测风站实测风速序列为例,提出基于经验模式分解法与自适应神经模糊推理法混合建模的铁路风速混合预测算法,并将提出的智能预测混合算法与其他预测算法性能进行比较。
1 混合算法的建模原理
将混合算法命名为经验模式-自适应神经模糊推理法(EMD-ANFIS algorithm),结合如图1所示的建模流程,对本混合法进一步阐述如下:1) 选择经验模式分解法对实测原始铁路风速进行分解和重构,减低后期分解层上所建预测模型的拟合难度;2) 利用自适应神经模糊推理法对各模式分解层建立超前几步的预测模型;3) 加权各个分解层的风速预测值。
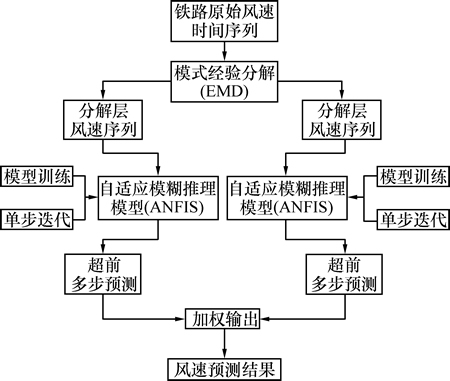
图1 混合建模框架
Fig. 1 Framework of hybrid modeling
2 建模过程
2.1 原始风速
运用本文提出的混合算法对我国青藏铁路沿线某重点监控点的大风风速模拟检验序列{X(t)}(共计500个采样点序列)进行建模与预测,如图2所示。本文取原始风速序列的前400个数据用于建立预测模型,后100个数据用于检验模型。
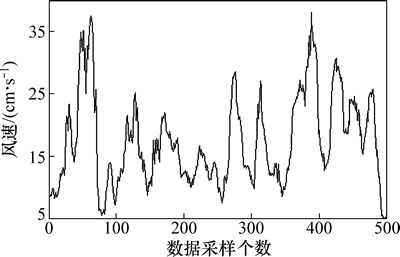
图2 {X(t)}风速
Fig. 2 Wind speed of {X(t)}
2.2 经验模式分解法的计算步骤
本文采用已有标准的经验模式分解计算步骤[18]。
步骤1:确定原始风速时间序列{X(t)}的所有局部极值点,利用3次样条曲线形成上、下包络线。
步骤2:依次计算上包络线和下包络线的平均值 ,然后按照下式求出信号残差序列{H(t)}:
,然后按照下式求出信号残差序列{H(t)}:
 (1)
(1)
式中:t为风速时间序列个数;L为风速时间序列的总长度。不断重复以上操作,直到某残差满足模式分量要求为止,则将其记为第1个模式分解量序列{C1(t)},然后将原始信号扣除序列{C1(t)}后当作新非平稳序列继续重复上述分解环节,直到逐步分解出{C2(t)},{C3(t)},…,{Cn-1(t)},{Cn(t)}等后续序列,将经过n次循环后剩下的最终残差序列记为{R(t)}。在实际运用时,当残差序列已经无法收敛时,按照下式确定终止循环条件:
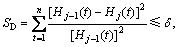
 (2)
(2)
式中:SD为分解收敛系数,可取SD=0.2~0.5,本文取为0.2;j为经验模式分解的循环迭代次数。
步骤3:经过经验模式分解,原始风速信号等于各分解层序列之和,即
 (3)
(3)
式中:{X(t)}为原始风速;{Ci(t)}为各个分解层;n为分解层数目;{R(t)}为原始风速时间序列经过分解后剩下的残差序列。
运用上述经验模式分解法对图2所示的实测铁路非平稳原始风速序列进行分解计算,最终获得如图3所示的分解层风速子序列。从图3可知:原始铁路风速序列被转换成为9个模式分解量序列和1个残差序列。与小波分析法等其他信号分解方法不同,经验模式分解法不需要人为地选择分解层数和分解函数,这样有效地避免了由于人为误选所造成的的信号成分丢失,从而间接地提高了后期预测模型的计算精度。
2.3 自适应神经模糊推理法的建模步骤
自适应神经模糊推理法(adaptive neural fuzzy inference system,ANFIS)有效地将模糊推理和神经网络有机结合。它属于一类典型的多层前向反馈神经网络模型[19-20]。本文采用的ANFIS结构如图4所示。
本文选择双边高斯作为隶属度函数,网络的最大学习训练步数为50,模型的目标最小均方误差为0.001。
2.4 风速分解层的预测结果
对各个分解层风速序列的前400个数据依次完成ANFIS建模与训练,然后利用ANFIS模型对各层的后100个数据依次完成超前单步预测计算,结果如图5~10所示。
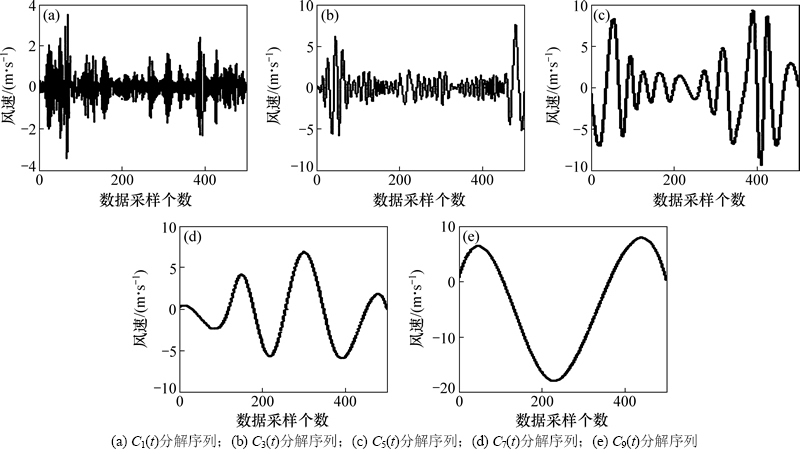
图3 原始风速序列{X(t)}的经验模式分解结果
Fig. 3 Decomposed results of original wind speed series {X(t)} by mode empirical decomposition algorithm
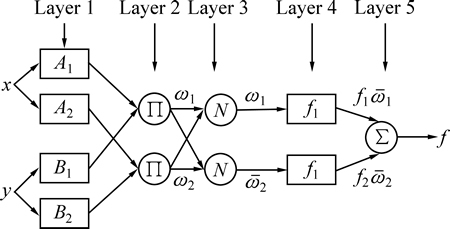
图4 两输入-单输出的ANFIS结构
Fig. 4 ANFIS structure of two inputs-single outputs
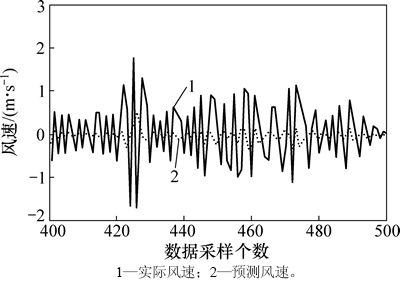
图5 {C1(t)}序列的单步预测结果
Fig. 5 Single-step predicted results of {C1(t)} series
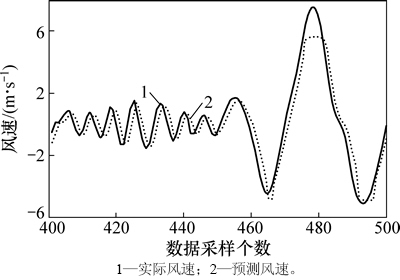
图6 {C3(t)}序列的单步预测结果
Fig. 6 Single-step predicted results of {C3(t)} series
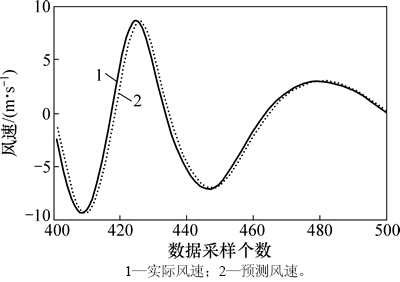
图7 {C5(t)}序列的单步预测结果
Fig. 7 Single-step predicted results of {C5(t)} series
2.5 各分解层预测结果加权计算
采取式(9)对分解层进行加权计算。
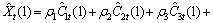
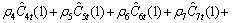
 (4)
(4)
为了充分比较所提出混合算法的优越性,分别采用单种自适应神经模糊推理模型、时序ARIMA模型和单种BP神经网络模型对同一段原始风速数据也进行超前多步预测计算,并将它们的预测结果与混合算法的结果进行比较输出,如图11~13所示。
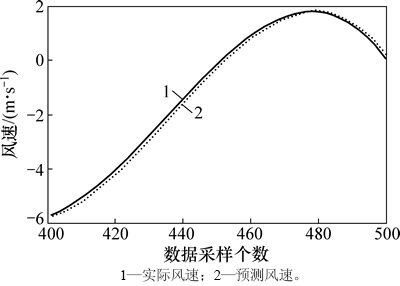
图8 {C7(t)}序列的单步预测结果
Fig. 8 Single-step predicted results of {C7(t)} series
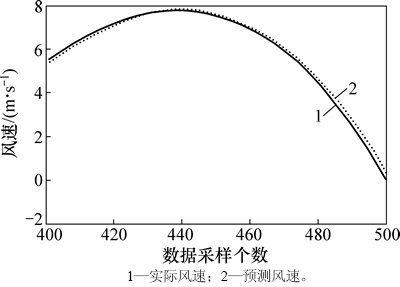
图9 {C9(t)}序列的单步预测结果
Fig. 9 Single-step predicted results of {C9(t)} series
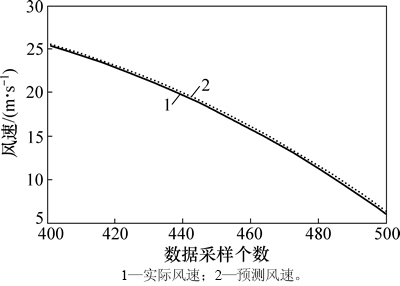
图10 {R9(t)}序列的单步预测结果
Fig. 10 Single-step predicted results of {R9(t)} series
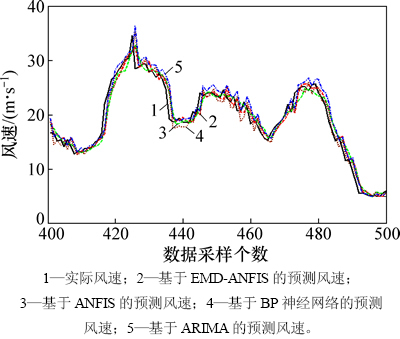
图11 {X(t)}序列的单步预测结果
Fig. 11 Single-step predicted results of {X(t)} series
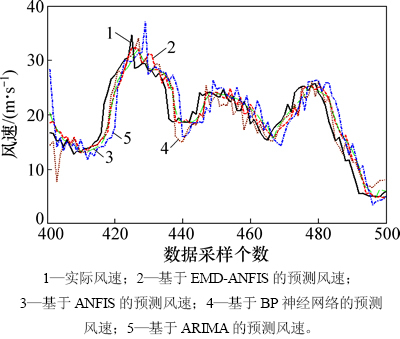
图12 {X(t)}序列的2步预测结果
Fig. 12 Two-step predicted results of {X(t)} series
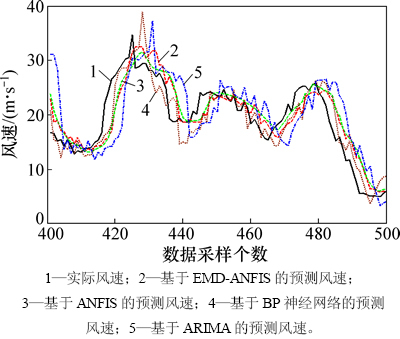
图13 {X(t)}序列的3步预测结果
Fig. 13 Three-step predicted results of {X(t)} series
3 优化算法预测结果分析
运用式(10)~(12)对图11~13中的几种不同算法的超前多步预测结果进行评估,结果如表1~4所示。此外,为了进一步分析经验模式分解法在混合算法中的贡献度,采用经验模式分解法对单种自适应神经模糊推理模型的性能优化比进行统计,如表5所示。
1) 平均绝对误差σ1:
 (5)
(5)
2) 平均相对误差σ2:
 (6)
(6)
3) 均方根误差σ3:
 (7)
(7)
分析图11~13和表1~4可知:混合算法所建模型的各项预测评价指标均优于其他3种经典的主流模型。单种自适应神经模糊推理模型优于BP神经网络模型,而后者优于时序ARIMA模型。以超前3步预测的结果为例,混合算法将单种自适应神经模糊推理模型的平均相对误差从16.26%提高到14.30%。BP神经网络模型和时序ARIMA模型的同类指标分别为16.53%和28.07%。
表1 混合算法(EMD-ANFIS)的预测性能
Table 1 Predicted performance of hybrid algorithm (EMD-ANFIS)
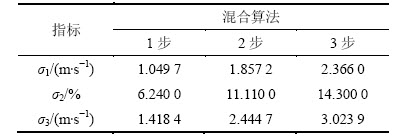
表2 单种ANFIS法的预测性能
Table 2 Predicted performance of single ANFIS
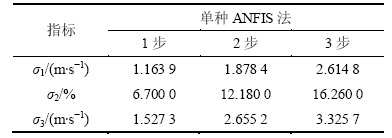
表3 BP网络的预测性能
Table 3 Predicted performance of BP network
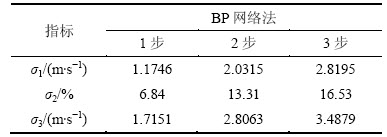
表4 ARIMA的预测性能
Table 4 Predicted performance of ARIMA
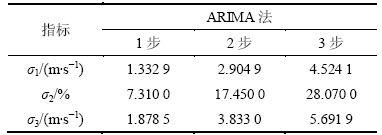
表5 EMD-ANFIS算法提高单种ANFIS模型的精度
Table 5 Improved accuracy of single ANFIS by EMD-ANFIS hybrid algorithm %
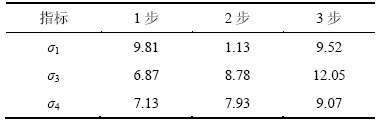
分析表5可知:随着超前预测步数的增加,经验模式分解法在混合算法中的贡献度也逐步提高。以平均相对误差为例,超前单步到3步的提高幅度分别达到6.87%,8.78%和12.05%。这表明本文所提出的混合算法在超前多步预测上体现出良好的算法性能。
4 结论
1) 提出的基于经验模式分解法-自适应神经模糊推理法的混合预测算法解决了铁路风速高精度超前多步预测难题,其超前单步、2步和3步的平均绝对相对误差分别为6.24%,11.11%和14.30%,高于铁路现场精度15%的要求。混合算法不仅考虑了经验模式分解法的信号分解与辨识能力,而且也兼顾了自适应神经模糊推理法的非线性隐射能力,能够实现对铁路实测非平稳风速的高精度追踪和预测。
2) 混合算法的预测精度随着模型步数的增加而降低。此外,相对于其他算法如时间序列分析法、单种自适应神经模糊推理法等,混合算法的计算难度没有明显增大,保持了计算简单的特点。因此,可以将混合算法方便地运用于相关的风速预测系统中。
参考文献:
[1] 高广军, 田红旗, 姚松, 等. 兰新线强横风对车辆倾覆稳定性的影响[J]. 铁道学报, 2004, 26(4): 36-40.
GAO Guangjun, TIAN Hongqi, YAO Song, et al. Effect of strong cross-wind on the stability of trains running on the Lanzhou—Xinjiang railway line[J]. Journal of the China Railway Science, 2004, 26(4): 36-40.
[2] 刘辉, 田红旗, 李燕飞. 基于小波分析法与神经网络法的非平稳风速信号短期预测优化算法[J]. 中南大学学报(自然科学版), 2011, 42(9): 2704-2711.
LIU Hui, TIAN Hongqi, LI Yanfei. Short-term forecasting optimization algorithm for wind speed from wind farms based on wavelet analysis method and rolling time series method[J]. Journal of Central South University (Science and Technology), 2011, 42(9): 2704-2711.
[3] 李燕飞, 田红旗, 刘辉. 高速铁路开孔式挡风墙外形优化研究[J]. 中南大学学报(自然科学版), 2011, 42(10): 3207-3212.
LI Yanfei, TIAN Hongqi, LIU Hui. Optimization of windbreak wall with holes in high-speed railway[J]. Journal of Central South University (Science and Technology), 2011, 42(10): 3207-3212.
[4] CHELI F, GIAPPINO S, ROSA L, et al. Experimental study on the aerodynamic forces on railway vehicles in presence of turbulence[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 123: 311-316.
[5] BIADGO A, SIMONOVIC A, SVORCAN J, et al. Aerodynamic characteristics of high speed train under turbulent cross winds: A numerical investigation using unsteady-RANS method[J]. FME Transactions, 2014, 42(1): 10-18.
[6] 杨明智, 袁先旭, 鲁寨军, 等. 强侧风下青藏线列车气动性能风洞试验研究[J]. 实验流体力学, 2008, 22(1): 76-79.
YANG Mingzhi, YUAN Xianxu, LU Zhaijun, et al. Experimental study on aerodynamic characteristics of train running on Qinghai—Tibet railway under cross winds[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(1): 76-79.
[7] WAGNER S, EHRENFRIED K, DILLMANN A. Numerical simulation of train-tunnel entry using a beam in time domain[M]//New Results in Numerical and Experimental Fluid Mechanics VIII. Heidelberg, Berlin: Springer, 2013: 739-746.
[8] 熊小慧, 梁习锋. 横风作用下货车篷布结构强度计算[J]. 中南大学学报(自然科学版), 2012, 43(8): 3280-3286.
XIONG Xiaohui, LIANG Xifeng. Numerical simulation of tarpaulin structural strength of railway vehicle under cross wind condition[J]. Journal of Central South University (Science and Technology), 2008, 39(8): 3280-3286.
[9] ALLAIN E, PARADOT N. Aerodynamics in train cross wind studies[J]. International Journal of Aerodynamics, 2014, 4(1): 10-23.
[10] LI Tian, ZHANG Jiye, ZHANG Weihua. Co-simulation of high-speed train fluid-structure interaction dynamics in crosswinds[J]. Journal of Vibration Engineering, 2012, 25(2): 138-145.
[11] GILBERT T, BAKER C J, QUINN A. Gusts caused by high-speed trains in confined spaces and tunnels[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 121: 39-48.
[12] BAKER C. A framework for the consideration of the effects of crosswinds on trains[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 123: 130-142.
[13] BAKER C, CHELI F, ORELLANO A, et al. Cross-wind effects on road and rail vehicles[J]. Vehicle System Dynamics, 2009, 47(8): 983-1022.
[14] HOPPMANN U, KOENIG S, TIELKES T, et al. A short-term strong wind prediction model for railway application: design and verification[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(10): 1127-1134.
[15] KOBAYASHI N, SHIMAMURA M. Study of a strong wind warning system[J]. JR East Technical Review, 2003(2): 61-65.
[16] 潘迪夫, 刘辉, 李燕飞, 等. 青藏铁路格拉段沿线风速短时预测方法[J]. 中国铁道科学, 2009, 29(5): 129-133.
PAN Difu, LIU Hui, LI Yanfei, et al. A short-term forecast method for wind speed along Golmud—Lhasa section of Qinghai—Tibet railway[J]. China Railway Science, 2009, 29(5): 129-133.
[17] 刘辉, 田红旗, 李燕飞. 基于小波分析法与滚动式时间序列法的风电场风速短期预测优化算法[J]. 中南大学学报(自然科学版), 2010, 41(1): 370-375.
LIU Hui, TIAN Hongqi, LI Yanfei. Short-term forecasting optimization algorithm for wind speed from wind farms based on wavelet analysis method and rolling time series method[J]. Journal of Central South University (Science and Technology), 2010, 41(1): 370-375.
[18] CHEN Chinyu, GUO Shumei, CHANG Wwisheng, et al. An improved bidimensional empirical mode decomposition: A mean approach for fast decomposition[J]. Signal Processing, 2014, 98: 344-358.
[19] XU Zhe, MAO Zhizhong. Element yield rate prediction in ladle furnace based on improved GA-ANFIS[J]. Journal of Central South University, 2012, 19(9): 2520-2527.
[20] 董明宇, 刘民, 吴澄. 带并行机调度问题中基于ANFIS的自适应算法[J]. 控制工程, 2005, 12(3): 203-206.
DONG Mingyu, LIU Min, WU Cheng. An ANFIS based adaptive algorithm for job shop scheduling problem with parallel machines[J]. Control Engineering of China, 2005, 12(3): 203-206.
(编辑 陈灿华)
收稿日期:2015-02-24;修回日期:2015-04-22
基金项目(Foundation item):国家自然科学基金资助项目(51308553);国家高铁联合基金资助项目(U1134203,U1334205);湖南省教育厅科学研究项目(省优秀博士学位论文奖励专项);中南大学升华育英人才计划项目(502034011);中南大学研究生自主探索创新项目基金资助项目(2013zzts041)(Project (51308553) supported by the National Natural Science Foundation of China; Projects (U1134203, U1334205) supported by the National High Speed Railway; Project supported by the Science Research of Education Department of Hunan Province (Provincial Outstanding Doctoral Dissertation Award); Project (502034011) supported by the Sublimation Yuying Talent of Central South University; Project (2013zzts041) supported by the Central South University Graduate Students Independently Exploratory Innovative Fund)
通信作者:刘辉,教授,博士生导师,从事交通安全与智能控制、风工程监控与预测等研究;E-mail:csuliuhui@csu.edu.cn