基于高斯混合PHD滤波的多机动扩展目标跟踪
田森平,周波,戚其丰
(华南理工大学 自动化科学与工程学院,广东 广州,510640)
摘要:针对多机动椭圆目标的跟踪问题进行研究,建立一种非线性跳变马尔科夫系统模型,继而提出一种新的扩展目标高斯混合概率假设(ET-GM-PHD)滤波算法。新算法引用无损变换(UT)法,解决模型的非线性性,采用一种基于距离的启发式分区策略对观测集合进行了分区,该分区策略简便易操作而且能很大程度地降低算法的计算量。仿真实例表明:新算法比未进行分区的标准GM-PHD滤波算法更加强健有效。
关键词:扩展目标;跳变马尔科夫系统模型;无损变换;GM-PHD
中图分类号:TN713 文献标志码:A 文章编号:1672-7207(2013)12-4923-07
Gaussian mixture PHD filter based tracking multiple Maneuvering extended targets
TIAN Senping, ZHOU Bo, QI Qifeng
(College of Automation Science and Engineering, South China University of Technology, Guangzhou 510640, China)
Abstract: The problem of tracking multiple maneuvering elliptical targets was studied and a nonlinear jump Markov system model was established. Then a new Gaussian mixture PHD filter for extended targets (ET-GM-PHD) was proposed. This ET-GM-PHD filter adopted the unscented transform technique to overcome the nonlinearity of model, and was carryed out by using a heuristic measurement partition scheme based on the distances between the measurements. This partition scheme is easy, operable and can greatly reduce the computation of the algorithm. Simulation results show that the proposed algorithm is more effective and robust than the standard GM-PHD filter without measurement partition.
Key words: extended targets; jump Markov system models; unscented transform; GM-PHD
标准的目标跟踪一般都将目标近似看作“数学点”,建立相应的点模型(相对于目标大小,目标与传感器的距离充分远),这意味着可假定每个时刻每个目标最多只能得到一个观测。近来,随着传感器技术的发展,扩展目标跟踪获得了原来越多的关注。每个时刻每个目标可以得到多个观测的那种类型的目标称为扩展目标。扩展目标跟踪不仅考虑目标的位置信息,也考虑目标的空间大小或形状等信息。一般来说,扩展目标跟踪可通过建立相应的模型来提取目标信息,例如Angelova等[1]提出了椭圆模型。然而大多数文献在建立的模型基础上提出的跟踪算法都是基于单扩展目标跟踪及数据融合的,往往不能很好地解决杂波环境下目标数可以随机变化的扩展目标跟踪问题。Mahler[2-4]提出了基于有限集统计学的概率假设密度(PHD)[3]滤波算法,避免了传统的多目标跟踪算法带来的计算量爆炸问题。文献[4]中提出了适用多扩展目标跟踪的PHD算法(ET-PHD),该算法假定每个时刻由目标产生的观测数目服从泊松分布,它将观测集合分成了一系列观测集单元,进而在观测集单元的基础上建立起相应的PHD滤波算法。随后,以Vo等[5-6]提出了通过简便易操作的高斯混合的方式近似实现PHD算法。对于机动目标的跟踪,周宏仁等[8-9]研究了机动目标的跟踪,表明建立的模型应为可跳转的马尔科夫系统模型(JMS)。Punithakumar等[10]提出采用多模型PHD算法可跟踪多机动标准目标,Pasha等[6]建议采用多模型GM-PHD算法解决多机动标准目标的跟踪问题。近来,建立在随机有限集 基础上的多目标跟踪技术有了较快发展,但是对于多扩展目标跟踪技术的研究却不多。Granstrom等[11]提出了一种基于距离原则的观测集分区策略。Granstrom等[12]研究了矩形和椭圆2种类型的多扩展目标跟踪问题,提出了适于这2种扩展目标的ET-PHD算法。Li等[13]针对多机动扩展目标跟踪问题进行研究,建立了一类线性JMS模型,提出了一种高斯混合实现ET-PHD算法(即ET-GM-PHD),该算法采用了BFG[14]近似法表达模型的动态性。连峰等[15]证明了在杂波强度先验已知且扩展目标的期望测量个数连续有界的假设条件下, 若GM-PHD滤波器的高斯分量数趋于无穷多, 那么它一致收敛于真实的ET-PHD 滤波器。本文作者研究的对象是一类多机动椭圆目标,相比Li等[13]所建立的线性JMS模型,文中建立的是一类适用范围更加广泛的非线性JMS模型。采用多模型混合的方式较好地表达了模型的动态性。算法中运用了无损变换(UT)[16]法来处理模型的非线性问题,而对于观测集合的分区,采用Granstrom等[11]提出的启发式分区策略,该分区策略很好地减少了ET-PHD滤波的计算量。最后,通过实例仿真,对比了新算法和标准的GM-PHD算法得到的位置状态估计、目标数目估计和OSPA距离[17](用来评价多目标误差距离),进一步表明了新算法在解决多扩展机动目标跟踪问题上的强健性和有效性。
基础上的多目标跟踪技术有了较快发展,但是对于多扩展目标跟踪技术的研究却不多。Granstrom等[11]提出了一种基于距离原则的观测集分区策略。Granstrom等[12]研究了矩形和椭圆2种类型的多扩展目标跟踪问题,提出了适于这2种扩展目标的ET-PHD算法。Li等[13]针对多机动扩展目标跟踪问题进行研究,建立了一类线性JMS模型,提出了一种高斯混合实现ET-PHD算法(即ET-GM-PHD),该算法采用了BFG[14]近似法表达模型的动态性。连峰等[15]证明了在杂波强度先验已知且扩展目标的期望测量个数连续有界的假设条件下, 若GM-PHD滤波器的高斯分量数趋于无穷多, 那么它一致收敛于真实的ET-PHD 滤波器。本文作者研究的对象是一类多机动椭圆目标,相比Li等[13]所建立的线性JMS模型,文中建立的是一类适用范围更加广泛的非线性JMS模型。采用多模型混合的方式较好地表达了模型的动态性。算法中运用了无损变换(UT)[16]法来处理模型的非线性问题,而对于观测集合的分区,采用Granstrom等[11]提出的启发式分区策略,该分区策略很好地减少了ET-PHD滤波的计算量。最后,通过实例仿真,对比了新算法和标准的GM-PHD算法得到的位置状态估计、目标数目估计和OSPA距离[17](用来评价多目标误差距离),进一步表明了新算法在解决多扩展机动目标跟踪问题上的强健性和有效性。
1 研究对象及模型建立
本文研究一类在x-y平面上移动的椭圆目标,目标运动状态向量为: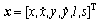 ,其中
,其中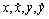 分别表示位置和速度;l表示椭圆目标长轴的长度;s表示椭圆短轴与长轴长度比例。已知传感器的坐标位置为(x0,y0),如图1所示。
分别表示位置和速度;l表示椭圆目标长轴的长度;s表示椭圆短轴与长轴长度比例。已知传感器的坐标位置为(x0,y0),如图1所示。
假定所有目标在一个平面上移动,速度向量和长轴平行。由图1可得:椭圆目标下延伸的长度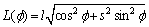 ,其中
,其中 表示长轴方向与传感器视线的夹角。
表示长轴方向与传感器视线的夹角。
本文考虑的目标运动状态转移模型为一类非线性JMS模型:
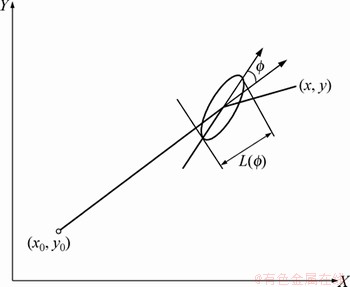
图1 机动椭圆目标
Fig. 1 Motor elliptic target
 (1)
(1)
其中: 表示状态空间上的一个非线性函数(也可以为线性函数[13]);wf,k表示独立的均值为0、方差为Qf,k(r)的过程高斯噪声;r表示特定的随时间变化的模型指示离散变量,其中r=1,…,Nm,系统模型可在Nm种模型中跳转。任意模型r下,考虑的观测模型为:
表示状态空间上的一个非线性函数(也可以为线性函数[13]);wf,k表示独立的均值为0、方差为Qf,k(r)的过程高斯噪声;r表示特定的随时间变化的模型指示离散变量,其中r=1,…,Nm,系统模型可在Nm种模型中跳转。任意模型r下,考虑的观测模型为:
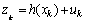 (2)
(2)
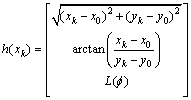 ,
,
 (3)
(3)
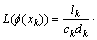
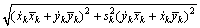 (4)
(4)
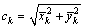 ,
,
 ,
,
其中:uk为独立的观测高斯噪声,其均值为0,方差为Rk。
2 新算法的提出
2.1 ET-PHD滤波算法
考虑一个目标数目和状态均随时间变化,传感器可以接收到随时间变化的观测的跟踪问题。使用2个随机有限集Xk和Zk分别表示k时刻的目标状态和观测,即:

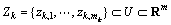
对于扩展目标,可能有多个观测来自同一个目标。假定满足以下条件:
(1) 所有目标之间和观测之间是独立的。目标在下一时刻仍存在的概率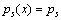 ,目标被检测到的概率为
,目标被检测到的概率为 。
。
(2) 预测多目标分布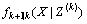 是泊松近似的:
是泊松近似的:
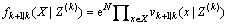 (5)
(5)
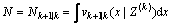 (6)
(6)
(3) 假定在k+1时刻由目标x产生的观测数目服从比率为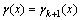 的泊松分布。若目标x产生一个有效观测集合Z′,那么似然函数为:
的泊松分布。若目标x产生一个有效观测集合Z′,那么似然函数为:
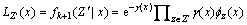 (7)
(7)
这里的 表示单观测似然。
表示单观测似然。
(4) 由每个目标产生的杂波误报数服从比例为λk+1的泊松分布。若扫描区域容积为Vs,则每次扫描得到的杂波误报观测数目期望为λk+1Vs。杂波观测的依空间分布假定为检测区域内的均匀分布ck+1(z)。
由文献[4]可得到ET-PHD的预测和更新公式。
预测公式:
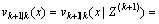
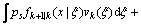
 (8)
(8)
其中: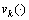 为后验强度函数(即PHD);
为后验强度函数(即PHD);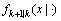 为单目标转移概率密度;bk+1(x)为自发出现(birth)新目标
为单目标转移概率密度;bk+1(x)为自发出现(birth)新目标 的强度函数;
的强度函数;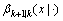 表示衍生新目标
表示衍生新目标 的强度函数。
的强度函数。
更新公式:
 (9)
(9)
当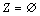 时:
时:
 (10)
(10)
当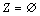 时:
时:
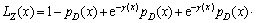
 (11)
(11)
 (12)
(12)
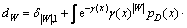
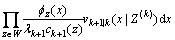 (13)
(13)
其中:|W|表示观测子集单元W中元素的个数;p表示观测集 的所有分区的总和。除空集外,p中的任意元素组成的所有可能的子集的并集就是Z′。表达式中
的所有分区的总和。除空集外,p中的任意元素组成的所有可能的子集的并集就是Z′。表达式中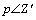 表示p将Z′分区,得到一系列非空观测子集单元W。随着观测集Z′中元素数目的增加,分区数目将变得十分多,使得计算量变大,故需寻找一种合理的分区原则降低算法计算量。
表示p将Z′分区,得到一系列非空观测子集单元W。随着观测集Z′中元素数目的增加,分区数目将变得十分多,使得计算量变大,故需寻找一种合理的分区原则降低算法计算量。
2.2 距离分区策略
采用一种简便易行的基于距离原则的分区策略对观测集合进行分区。大致过程为:对于给定的观测集合Zk,计算集合中任意2个观测 ,
,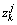 的马氏距离dij,然后对所有的dij进行排序,得到
的马氏距离dij,然后对所有的dij进行排序,得到 ,则观测集Zk就被分成了Nd个部分,每个分区都包括了一些观测子集单元,每个子集单元里至少有一个观测。实际上,dij服从一个自由度为3 的卡方分布,那么对给定的概率PG或置信水平α,查表可以得到相应的临界值,进而可通过一个卡方检验表明2个观测的靠近程度。若2个观测的距离
,则观测集Zk就被分成了Nd个部分,每个分区都包括了一些观测子集单元,每个子集单元里至少有一个观测。实际上,dij服从一个自由度为3 的卡方分布,那么对给定的概率PG或置信水平α,查表可以得到相应的临界值,进而可通过一个卡方检验表明2个观测的靠近程度。若2个观测的距离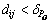 ,则认为这2个观测来自同一个目标,将它们划分到同一个观测子集单元W。因此只要合理地设定PG概率或置信水平α,就能得合理的分区集
,则认为这2个观测来自同一个目标,将它们划分到同一个观测子集单元W。因此只要合理地设定PG概率或置信水平α,就能得合理的分区集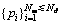 ,每个分区pi中包括一些观测单元
,每个分区pi中包括一些观测单元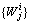 。注意:该分区策略只是一种简单启发式局部最优化方法,当目标之间相隔充分近时,它可能会把来自不同目标的观测归并到同一单元中。
。注意:该分区策略只是一种简单启发式局部最优化方法,当目标之间相隔充分近时,它可能会把来自不同目标的观测归并到同一单元中。
2.3 新ET-GM-PHD滤波算法
假定每个目标都服从式(1)非线性动态模型,传感器服从式(2)非线性观测模型。将状态与模型指示变量联合在一起,则得到联合强度函数:
 (14)
(14)
其中: 表示给定状态条件下的模型的分布;r为模型指示变量。而联合状态转移函数为:
表示给定状态条件下的模型的分布;r为模型指示变量。而联合状态转移函数为:
 (15)
(15)
其中: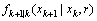 表示非线性状态转移函数;
表示非线性状态转移函数; 表示模型转移概率。
表示模型转移概率。
假定目标被检测到的概率pD(xk)满足:
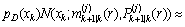
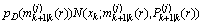
 (16)
(16)
其中: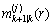 ,
, 和
和 分别表示相应的高斯分量均值、方差和分量数目。
分别表示相应的高斯分量均值、方差和分量数目。
假定k+1时刻模型r下自发出现 和衍生
和衍生 强度函数都是高斯混合的,即:
强度函数都是高斯混合的,即:
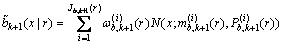 (17)
(17)
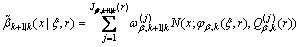 (18)
(18)
这里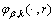 表示状态空间上一个给定的线性或非线性函数。则联合模型指示变量得自发出现
表示状态空间上一个给定的线性或非线性函数。则联合模型指示变量得自发出现 和衍生
和衍生 的强度函数分别为:
的强度函数分别为:
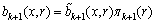 (19)
(19)
 (20)
(20)
其中: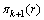 为自发出现
为自发出现 的模型概率分布;
的模型概率分布; 为目标衍生
为目标衍生 模型概率分布。
模型概率分布。
假定泊松比率γ(x)近似满足:


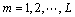 (21)
(21)
则就可导出ET-GM-PHD算法的关键步骤。
预测步:若在k时刻,已知后验强度函数为:
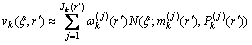 (22)
(22)
它的每个高斯分量 都和一个sigma点集合
都和一个sigma点集合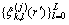 相关。
相关。
可得预测强度函数为以下近似高斯混合形式:
 (23)
(23)
由无损(UT)变换可知:由式(1)可得一个相关的均值为0、方差为 的sigma点集合
的sigma点集合 ,L为选取的点数目,n为状态维数,取L=2n,则:
,L为选取的点数目,n为状态维数,取L=2n,则:

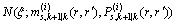 (24)
(24)
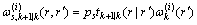 (25)
(25)
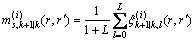 (26)
(26)
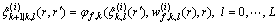 (27)
(27)
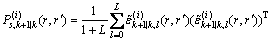 (28)
(28)
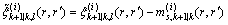 (29)
(29)
经无损(UT)变换,易知目标衍生 强度函数的每个混合成员j都包含一个均值为0、方差为
强度函数的每个混合成员j都包含一个均值为0、方差为 的sigma点集合
的sigma点集合 ,则
,则

 (30)
(30)
 (31)
(31)
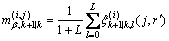 (32)
(32)
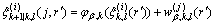 (33)
(33)
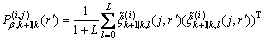 (34)
(34)
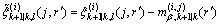 (35)
(35)
自发出现新目标 的预测强度函数为:
的预测强度函数为:
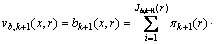
 (36)
(36)
分区步:运用距离分区策略对k+1时刻的观测集Zk+1分区,获得合理数目的观测子集单元。
更新步:假定预测强度函为:
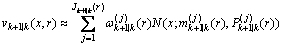 (37)
(37)
每个高斯分量都有一sigma点集合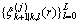 。则得更新强度函数的近似高斯混合形式为:
。则得更新强度函数的近似高斯混合形式为:
 (38)
(38)
其中:
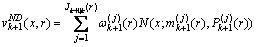 (39)
(39)
 (40)
(40)
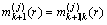 ,
,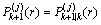 (41)
(41)
而:
 (42)
(42)
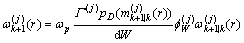 (43)
(43)
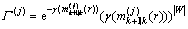 (44)
(44)
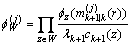 ,
, (45)
(45)
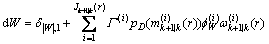 (46)
(46)
而对于每个观测子集单元W,通过无损变换(UT)得到似然函数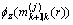 为:
为:
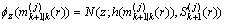 (47)
(47)
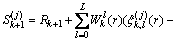
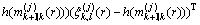 (48)
(48)
式中: 和
和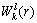 分别表示选取的sigma点和权重,对
分别表示选取的sigma点和权重,对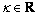 ,n表示状态维数,则
,n表示状态维数,则
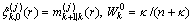 (49)
(49)
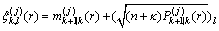
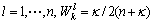 (50)
(50)
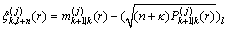
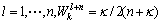 (51)
(51)
则相应高斯分量的均值和方差为:
 (52)
(52)
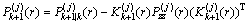 (53)
(53)
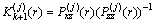 (54)
(54)
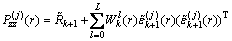 (55)
(55)
 (56)
(56)
 (57)
(57)
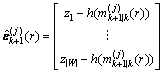 (58)
(58)
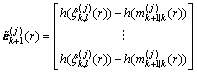 (59)
(59)
3 实例仿真
考虑一个椭圆目标可在监测区域的不同位置和时刻出现的二维场景。目标运动状态为前文所述状态。研究JMS模型为不同的3个转向加速模型。模型1和2为文献[13]中转向率Ω已知的线性模型,模型3为未知转向率Ω的模型(非线性模型),目标状态扩展为:
 (60)
(60)
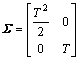 ,
,

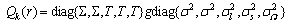 (61)
(61)
采样时间T=1 s,模型r=1的转向率Ω=0 (°)/s,对应过程噪声方差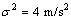 ,
, ,
,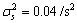 。模型r=2的转向率
。模型r=2的转向率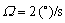 ,噪声方差
,噪声方差 ,
, ,
,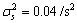 。模型3的
。模型3的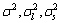 同模型2一样,
同模型2一样, 。模型转移概率矩阵:
。模型转移概率矩阵:
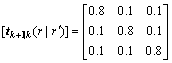 (62)
(62)
观测噪声方差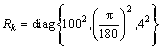 。传感器位置为(50,20),每个目标得到的观测数目泊松比率γ(x)=10。而ps=0.99,pD(x)=0.99。每个时刻单位区域内产生期望杂波数λk=1.6×10-3个,每次扫描整个监测区域可得到杂波误报数目为10个。目标自发出现的模型概率分布及强度函数分别为:
。传感器位置为(50,20),每个目标得到的观测数目泊松比率γ(x)=10。而ps=0.99,pD(x)=0.99。每个时刻单位区域内产生期望杂波数λk=1.6×10-3个,每次扫描整个监测区域可得到杂波误报数目为10个。目标自发出现的模型概率分布及强度函数分别为:
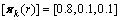 (63)
(63)
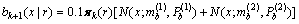
 ,
,
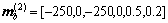 (64)
(64)
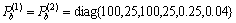 (65)
(65)
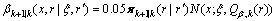 (66)
(66)
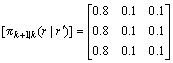 (67)
(67)
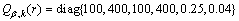 (68)
(68)
高斯分量参数设置方法引用文献[7]的方法,通过不断调整,最后设定修剪舍弃门限TTh=10-5,融合门限UTh=5,权重门限ωTh=0.5,最多保留分量数目Jmax=100个。
仿真平台是Matlab,其中目标1从时刻k=1 s初始位置为(-117,59)开始;目标2从k=1 s初始位置为(282,-97)开始;目标3从k=15 s初始位置为(83,-230)开始;目标4从k=50 s初始位置为(-905,-123)开始,均于k=100 s结束。评判标准是位置估计(横坐标和纵坐标)、数目估计和OSPA距离,仿真结果如下。
由图2可知:当目标较少时,标准GM-PHD与新算法都能获得较好的位置估计,随着目标数目增加且目标之间距离的靠近,新算法在位置估计跟踪上比标准的GM-PHD明显要准确得多。由图3可知:新算法能更好地拒绝杂波误报,获得准确估计数目。由图4可知:新算法得到的OSPA距离比GM-PHD要小得多。从而易得,新算法比未进行分割的标准GM-PHD滤波更准确有效。
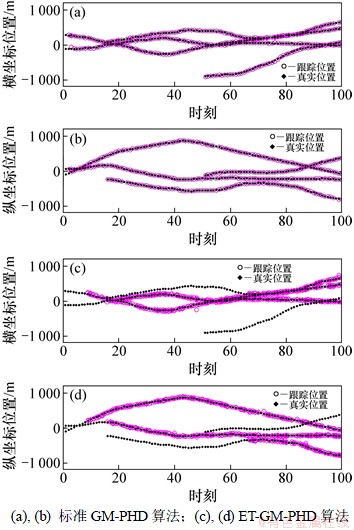
图2 目标位置估计对比
Fig. 2 Comparisons of target position estimation
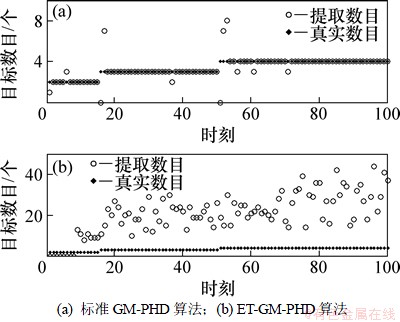
图3 目标数目估计对比
Fig. 3 Comparisons of target number estimation
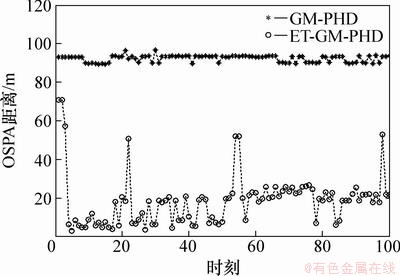
图4 OSPA距离对比
Fig. 4 Comparisons of OSPA distance
4 结论
(1) 针对一类椭圆目标跟踪问题,建立了一种适用范围比较广的非线性JMS系统模型,提出了一种新的ET-GM-PHD跟踪算法,该算法采用了一种简易可行的启发式分区策略对观测集进行了合理分区,并且运用了无损变换方法解决状态转移模型和观测模型的非线性问题。实验结果表明新算法在一个目标一次可产生多个观测的环境下也能很好地估计出目标的状态和数目,它相比标准的GM-PHD滤波具有更好地跟踪性能和实际工程应用价值。
(2) 本文所提算法需要假定每个目标每次产生的观测数目服从泊松分布,且假定目标之间相隔不是很近,一旦由目标产生的观测数目的分布情况未知或目标之间相隔充分近时,该算法就不能保证较好的跟踪性能。因此,寻找一种更合理的观测集分割策略及建立一种由目标得到的观测数目分布情况未知情形下的ET-GM-PHD滤波是今后值得研究的方向。
参考文献:
[1] Angelova D, Mihaylova L. Extended object tracking using Monte Carlo methods[J]. IEEE Transactions on Signal Processing, 2008, 56(2): 825-832.
[2] Mahler R P S. Statistical multisource-multitarget information fusion[M]. Norwood, MA, USA: Artech House Inc, 2007: 343-653.
[3] Mahler R P S, Martin L. Multi-target Bayes filtering via first-order multi-target moments[J]. IEEE Transactions Aerospace and Electronics Systems, 2003, 39(4): 1152-1178.
[4] Mahler R P S. PHD filters for nonstandard targets. I: Extended targets[C]//Proceedings of the 12th International Conference on Information Fusion. Seattle, WA, USA, 2009: 915-921.
[5] Vo B N, Ma W K. The Gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091-4104.
[6] Pasha A, Vo B N, Tuan H D, et al. A Gaussian mixture PHD filter for jump Markov system models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 919-936.
[7] 张洪建. 基于有限集统计学的多目标跟踪算法研究[D]. 上海: 上海交通大学电子、信息和电子工程学院, 2009: 13-95.
ZHANG Hongjian. Finite-set statistics based multiple target tracking[D]. Shanghai: Shanghai Jiao Tong University. College of Electronic, Information and Electrical Engineering, 2009: 13-95.
[8] 周宏仁, 敬忠良, 王培德. 机动目标跟踪[M]. 北京: 国防工业出版社, 1991: 1-300.
ZHOU Hongren, JING Zhongliang, WANG Peide. Maneuvering target tracking[M]. Beijing: National Defence Industry Press, 1991: 1-300.
[9] Li X R, Jilkov V P. Survey of maneuvering target tracking. Part V: multiple-model methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1255-1321.
[10] Punithakumar K, Kirubarajan T, Sinha A. Multiple model probability hypothesis density filter for tracking maneuvering targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 87-98.
[11] Granstrom K, Lundquist C, Orguner U. A Gaussian mixture PHD filter for extended target tracking[C]//Proceedings of the International Conference on Information Fusion. Edinburgh, UK, 2010: 1-8.
[12] Granstrom K, Lundquist C, Orguner U. Tracking rectangular and elliptical extended targets using laser measurements[C]//IEEE Proceeding of the 14th International Conference on Information Fusion. Chicago, Illinois, USA, 2011: 592-599.
[13] LI Wenling, JIA Yingmin, DU Junping, et al. Gaussian mixture PHD filter for multiple maneuvering extended targets tracking[C]//IEEE Conference on Decision and Control and European Control Conference. Orlando, FL, USA, 2011: 2411-2415.
[14] Hernandez M L, Ristic B, Farina A, et al. Performance measure for Markovian switching systems using best-fitting Gaussian distributions[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(2): 724-747.
[15] 连峰, 韩崇昭, 刘伟峰, 等. 高斯混合扩展目标概率假设密度滤波器的收敛性分析[J]. 自动化学报, 2012, 38(8): 1343-1352.
LIAN Feng, HAN Chongzhao, LIU Weifeng, et al. Convergence analysis of the Gaussian mixture extended-target probability hypo-thesis density filter[J]. Acta Automatic Sinica, 2012, 38(8): 1343-1352.
[16] Julier S J, Uhlmann J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE, 2004, 92(3): 401-422.
[17] Schuhmacher D, Vo B T, Vo B N. A consistent metric for performance evaluation of multi-object filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457.
(编辑 陈爱华)
收稿日期:2013-05-05;修回日期:2013-07-06
基金项目:国家自然科学基金资助项目(61374104);广东省自然科学基金资助项目(S2012010009675)
通信作者:戚其丰(1976-),男,浙江余姚人,讲师,从事图像处理与机器视觉研究;电话:13925136037;E-mail:qqfeng@gmail.com