Bi在Cu双晶中的非平衡晶界偏聚
来源期刊:中国有色金属学报(英文版)2014年第12期
论文作者:杨武强 徐 敏 梁剑雄 孟 晔 郑 磊
文章页码:4038 - 4043
关键词:铋;铜;偏聚;晶界;扩散
Key words:bismuth; copper; segregation; grain boundary; diffusion
摘 要:对Bi在Cu双晶中的晶界偏聚实验观察结果进行分析。利用平衡晶界偏聚(EGS)模型和非平衡晶界偏聚(NGS)模型,分别对500 °C时Bi在Cu双晶中的等温偏聚动力学和退火24 h的等时偏聚动力学进行研究。从定性分析和定量计算分析两方面推断出Bi的晶界偏聚特征与非平衡偏聚理论十分符合。根据非平衡晶界偏聚理论动力学模型,计算得到Bi-空位复合体扩散系数Dc=7.8×10-5exp[-1.46/(kT)],以及Bi原子的表观扩散系数DiA=7.66×10at+bexp[-1.76/(kT)],其中,a=8.45×10-8,b=-13.37。这些数据有助于对Cu合金中Bi所导致的脆化进行预测和控制的研究。
Abstract: The observations of grain-boundary segregation of Bi in Cu bicrystals were analyzed. According to equilibrium grain boundary segregation (EGS) model and non-equilibrium grain-boundary segregation (NGS) model, respectively, the segregation kinetics of isothermal annealing at 500 °C and that of isochronal annealing for 24 h of Bi in Cu bicrystals were investigated. By qualitative analysis and quantitative analysis, it is concluded that the grain-boundary segregation of Bi agrees well with the theory of NGS. Based on the kinetics model of NGS, some parameters that are useful to predicting and controlling the Bi-induced embrittlement in Cu alloys are calculated as follows: the diffusion coefficient of Bi-vacancy complexes Dc=7.8×10-5exp[-1.46/(kT)]; the apparent diffusion coefficient of Bi atoms DiA=7.66×10at+bexp[–1.76/(kT)], where a=8.45×10-8 and b=-13.37.
Trans. Nonferrous Met. Soc. China 24(2014) 4038-4043
Wu-qiang YANG1, Min XU1, Jian-xiong LIANG2, Ye MENG1, Lei ZHENG1
1. School of Materials Science and Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. Institute for Special Steels, Central Iron and Steel Research Institute, Beijing 100081, China
Received 16 February 2014; accepted 6 June 2014
Abstract: The observations of grain-boundary segregation of Bi in Cu bicrystals were analyzed. According to equilibrium grain boundary segregation (EGS) model and non-equilibrium grain-boundary segregation (NGS) model, respectively, the segregation kinetics of isothermal annealing at 500 °C and that of isochronal annealing for 24 h of Bi in Cu bicrystals were investigated. By qualitative analysis and quantitative analysis, it is concluded that the grain-boundary segregation of Bi agrees well with the theory of NGS. Based on the kinetics model of NGS, some parameters that are useful to predicting and controlling the Bi-induced embrittlement in Cu alloys are calculated as follows: the diffusion coefficient of Bi-vacancy complexes Dc=7.8×10-5exp[-1.46/(kT)]; the apparent diffusion coefficient of Bi atoms DiA=7.66×10at+bexp[–1.76/(kT)], where a=8.45×10-8 and b=-13.37.
Key words: bismuth; copper; segregation; grain boundary; diffusion
1 Introduction
Grain-boundary (GB) segregation affects various properties of the materials, such as temper embrittlement [1-4], intermediate temperature embrittlement [5-7], tensile ductility [8-10], and GB corrosion resistance [5,11,12]. Therefore, particular attention is paid to this phenomenon by many researchers. It is well known that GB segregation is classified into equilibrium segregation and non-equilibrium segregation [13,14]. The kinetic behavior of equilibrium grain-boundary segregation (EGS) was analyzed by MCLEAN [15] using diffusion theory. The non-equilibrium grain-boundary segregation (NGS) theory was proposed by AUST et al [16] and ANTHONY [17]. The kinetic model of NGS was given by FAULKNER [18] and XU et al [13,19].
In 1985, FRACZKIEWICZ and BISCONDI [20] studied the GB segregation of Bi in Cu bicrystals (containing 0.005% Bi, mole fraction). The isotherm at 500 °C revealed that the Bi content at GB gradually increased, reaching its maximum after annealing for 24 h and then decreased slowly (Fig. 1(a)). They [20] considered that the EGS of Bi occurred and the decrease in Bi content at GB was caused by precipitation. However, they also confirmed that intergranular particles were observed by the scanning electron microscope only in the samples annealing for 10 d. Therefore, the decrease in Bi content at GB after annealing for 24 h cannot be attributed to the formation of intergranular precipitates which was observed after annealing for 10 d. Besides, the isochrone of Bi segregation for 24 h showed that with the elevation of temperature, GB segregation of Bi increased gradually, reaching its maximum at around 500 °C and then decreased slowly (Fig. 1(b)). Based on EGS theory, they [20] considered that the heat treatment time was too short to achieve the maximum segregation at temperatures below 500 °C while it seemed to be enough to achieve a level close to the maximum in the temperature range of 500-650 °C. It is noteworthy that the NGS theory was successfully applied to explaining the maximum of embrittling isochrone of steels [1,13]. Therefore, the explanation of FRACZKIEWICZ and BISCONDI [20] by EGS theory seems to be invalid. In these cases, the segregating behavior of Bi in Cu bicrystals needs to be verified.
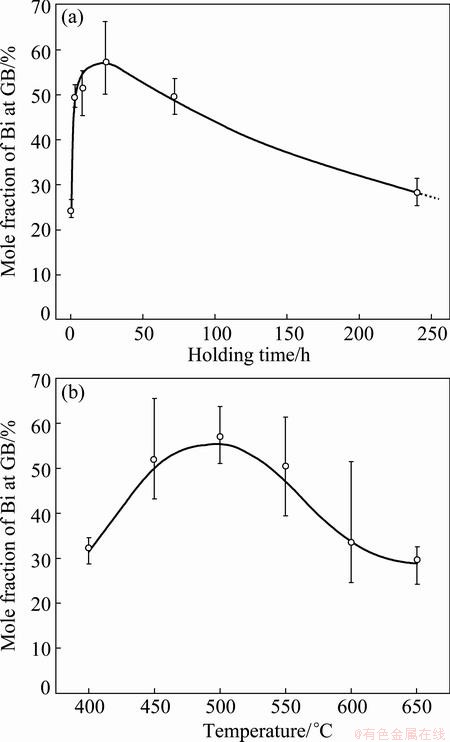
Fig. 1 Isothermal curve of Bi segregation in Cu bicrystals annealing at 500 °C (a) and isochronal curve annealing for 24 h (b) [20]
The present work is thus carried out to determine the segregating behavior of Bi in Cu bicrystals by the experimental results of FRACZKIEWICZ and BISCONDI [20]. It is found that the grain boundary segregation of Bi agrees well with the theory of NGS. On this basis, the diffusion coefficients of Bi-vacancy complexes and Bi atoms are calculated, which are helpful to predicting and controlling the Bi-induced embrittlement in Cu alloys.
2 Kinetic models of GB segregation
2.1 Kinetic model of EGS
MCLEAN [15] proposed a model for EGS and derived thermodynamic and dynamic equations. The thermodynamic equation is
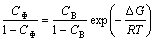 (1)
(1)
where CΦ is the equilibrium concentration of solute atoms at GB; CB is the bulk concentration of solute atom; ΔG is the molar Gibbs energy of GB segregation of solute atom. The dynamic equation of EGS is
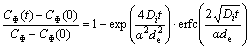 (2)
(2)
where CΦ(t) is the GB concentration after time t at a certain temperature T; CΦ(0) is the initial GB concentration; Di is the diffusion coefficient of the solute at a certain temperature; α is the equilibrium ratio CΦ/CB; de is the GB thickness. From Eq. (2) it is clear that the GB concentration increases gradually from an initial concentration CΦ(0) to a final equilibrium concentration CΦ as time extends.
2.2 Kinetic model of NGS
The NGS is considered to result from the formation of solute-vacancy atom complexes in the matrix, where solute atom, vacancy and their recombined complex are in local equilibrium [13,19]. When a sample is hold at a higher temperature Ti and then annealed isothermally at a certain lower temperature Ti+1 at once, the diffusion of complexes toward the GB and the reverse diffusion of solute atoms from the GB will be induced. At a critical time, these two diffusions balance with each other and the solute atom content at GB reaches a maximum. When the holding time is shorter than the critical time, the diffusion of complexes to the GB will be the dominant process and is referred as the segregation process. When the holding time is longer than the critical time, the reverse diffusion of solute atoms will be the dominant process and is referred as the de-segregation process. The critical time is the most characteristic aspect of NGS and the basic criterion to distinguish NGS from EGS [1,8,13]. A formula for the critical time, tc, is given by FAULKNER [18] and XU et al [13,19] as
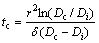 (3)
(3)
where r is the grain radius; Dc represents the diffusion coefficient of the complex; δ denotes the critical time constant.
XU et al [13,19,21] established the isothermal kinetic model of NGS for two processes. For the segregation process (t
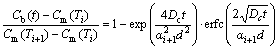 (4)
(4)
For the de-segregation process (t>tc), the NGS kinetic equation is given as [13,19,21]
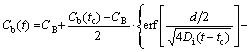
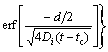 (5)
(5)
where Cb(t) is the solute atom content at the GB as a function of t at temperature Ti+1; Cm(Ti) is the maximum solute content at the GB at temperature Ti; d is the width of the concentrated layer; αi+1=Cm(Ti+1)/CB; Cb(tc) is the solute content at the GB at critical time tc and temperature Ti+1.
3 Discussion
3.1 Verification of segregating behavior of Bi in Cu bicrystals
According to EGS theory, the isothermal kinetics and isochronal kinetic curves of Bi segregation in Cu bicrystals were calculated and shown in Fig. 2. The parameters used for the calculation are listed in Tables 1 and 2. It can be seen from Fig. 2(a) that during isothermal annealing at 500 °C the content of Bi at the GB gradually approaches an equilibrium value CΦ= 64.4% as time goes to infinity. On the contrary, the experimental results show a definite maximum. Thus, the trend of the calculated curve does not fit to the experimental results. From Fig. 2(b) it can also be seen that during isochronal annealing for 24 h the Bi segregation decreases progressively as the temperature increases, which obviously deviates from the experimental data in the temperature range of 400-500 °C. Based on Fig. 2, it can be reasonably concluded that EGS of Bi in Cu bicrystals does not occur.
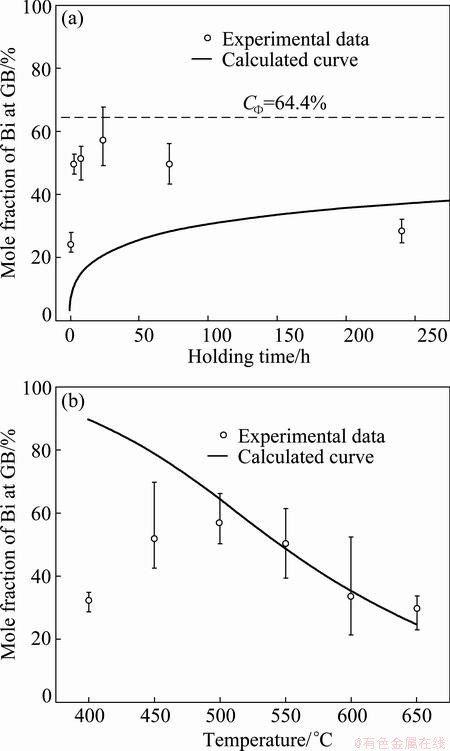
Fig. 2 Isothermal curve of Bi segregation annealing at 500 °C (a) and isochronal curve annealing for 24 h (b) calculated with EGS theory
Table 1 Parameters and corresponding values used for calculations by EGS theory
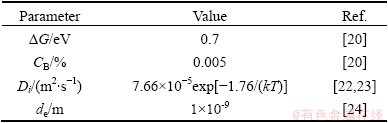
Table 2 Parameters and corresponding values used for calculations by NGS theory
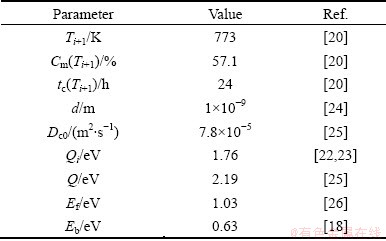
It is noteworthy that the critical time is the most characteristic aspect of NGS and the basic criterion to distinguish NGS from EGS. At the critical time, the GB segregation reaches the maximum. Thus, if NGS occurs, the GB segregation will increase first, reach the maximum at critical time, decrease gradually, and approach to thermodynamic level finally. Clearly, the isothermal kinetic curve of Bi segregation in Fig. 1(a) shows the same tendency and gives the support to the occurrence of NGS of Bi in Cu bicrystals. Besides, the NGS of Bi can induce not only the isothermal maximum, but also the isochronal one. According to Eq. (3), the critical time for the maximum GB segregation of Bi decreases when the temperature is elevated [1,8,13]. At a rather low temperature, the critical time can be much longer than the fixed annealing time of 24 h. As a consequence, the diffusion of complexes towards GBs is dominant and the Bi content at the GB is far from the maximum. So, the Bi content at the GB is low. As the temperature increases, both diffusion processes become accelerated, and therefore the critical time becomes shorter. At 500 °C, the critical time equals the annealing time of 24 h (Fig. 1(a)). Thus, the content of Bi at the GB reaches its maximum. With further increase in temperature, the critical time becomes even shorter than 24 h. Thus, the reverse diffusion of Bi becomes already dominant during the fixed holding time of 24 h. In consequence, segregation of Bi at the GB decreases. From the qualitative analysis of both isothermal and isochronal kinetics of Bi segregation, it can be confirmed that the segregating behavior of Bi in Cu bicrystals is NGS.
3.2 Calculation of isotherm of NGS of Bi
Since the segregation of Bi at GB in Cu bicrystals is NGS, the detailed knowledge of NGS of Bi must be helpful to predicting and controlling the Bi-induced embrittlement in Cu alloys, for example, intermediate temperature embrittlement [27].
In the experiment of FRACZKIEWICZ and BISCONDI [20], the samples were quenched at solution temperature of 950 °C. Here, it is considered that the content of Bi at the GB reaches the equilibrium during solution treatment at temperature Ti. Consequently, Cm(Ti) (equal to CΦ) can be obtained by Eq. (1). As for the maximum content of Bi at temperature Ti+1, Cm(Ti+1), it can be assumed to be equal to Cb(tc) which is the content of Bi at the GB at the critical time [28,29]. According to the experimental results, the critical time tc at 500 °C can be determined as 24 h. All parameters are listed in Tables 1 and 2. Substituting these parameters into Eqs. (4) and (5), the diffusion coefficients of Bi-vacancy complex and Bi atoms at different isothermal holding time were simulated and shown in Table 3. It is worth mentioning that the simulated diffusion coefficients in Table 3 are not the real diffusion coefficients of the complexes or the solute in the matrix. Actually, they are apparent diffusion coefficients according to the NGS model since diffusions of complexes towards the GB and solute atoms towards grain interiors occur simultaneously [13].
Table 3 Simulated values of diffusion coefficients of Bi- vacancy complex and Bi atoms
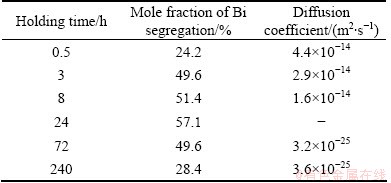
3.2.1 Segregation process of NGS of Bi
It is well known that the diffusion coefficient of the complex, Dc, is the most important parameter to characterize the NGS. However, its value of Bi-vacancy complex in Cu alloy has not been determined so far. Theoretically, the apparent diffusion coefficient of complexes will decrease as annealing time extends in the segregation process since diffusions of complexes and solute atoms occur simultaneously. Whereas, the diffusion of Bi atoms towards grain interiors is far slower than that of complexes towards GB, the apparent diffusion coefficient of complexes can be assumed to be nearly constant and as the real one [13,29,30]. In this case, the average value, Dc=2.97×10-14 m2/s, of the apparent diffusion coefficients (see Table 3) can be taken as the real diffusion coefficient of Bi-vacancy complexes in Cu alloys. By using this value, the kinetic curve of NGS of Bi in segregation process was calculated (Curve I in Fig. 3). It can be seen from Fig. 3 that Curve I fits well with the experimental data, which confirms the reliability of this assumption.
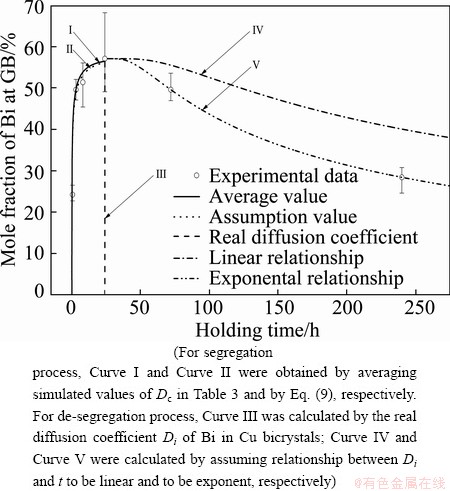
Fig. 3 Isothermal kinetics curves of Bi segregation in Cu bicrystals at 500 °C calculated by NGS theory
Although the diffusion coefficient of Bi-vacancy complexes, Dc, is determined, it is only a specified value at 500 °C. A general formula for Dc in Cu alloys at any given temperature is still in demand. According to Arrehenius equation,
Dc=Dc0exp[-Qc/(RT)] (6)
the diffusion coefficient of solute-vacancy complex depends on the activation energy Qc and the frequency factor Dc0. XU et al [21] assumed that Qc can be estimated by
Qc=(Qi+Em)/2 (7)
where Qi and Em are the activation energies of solute diffusion and vacancy migration, respectively. Since vacancies are formed when the samples are maintained at the higher temperature, Em can be considered as
Em=Q-Ef (8)
where Q is the activation energy for self-diffusion of solute; Ef is the vacancy formation energy [31]. XU et al [21] assumed that Dc0 is approximately replaced by the frequency factor of self-diffusion. In this case, the diffusion coefficient of Bi-vacancy complex is expressed as
Dc=Dc0exp[-(Qi+Q-Ef)/(2RT)] (9)
Substituting the parameters listed in Tables 1 and 2 into Eqs. (4) and (9), it is obtained that
Dc=7.8×10-5exp[-1.46/(kT)] (10)
By Eq. (10), the kinetic data of segregation process of Bi were calculated (Curve II in Fig. 3). It is clear that Curve II also fits well with the experimental results, which confirms the reliability of the assumption of XU et al [21]. Thus, the Arrehenius equation for the diffusion coefficient of Bi-vacancy complex in Cu alloy is obtained.
3.2.2 De-segregation process of NGS of Bi
According to the NGS model, the reverse diffusion of Bi atoms to grain interior dominates the de-segregation process, and the apparent diffusion coefficient will be equal to the real diffusion coefficient finally. Therefore, the preferred way to calculate the kinetics of de-segregation process of the NGS of Bi is to replace the apparent diffusion coefficient DiA by the real diffusion coefficient Di (Table 1). On this basis, the kinetic curve of NGS of Bi in the de-segregation process is calculated (Curve III in Fig. 3). It is seen that the calculated segregation level (Curve III in Fig. 3) drops dramatically to nearly zero. Therefore, the real diffusion coefficient is quite different from the apparent one and cannot be used for the whole de-segregation process.
It can be known from the NGS model that the apparent diffusion coefficient of solute atoms DiA will increase as annealing time t extends in the de-segregation process. The simulated values of DiA of Bi in Table 3 indicate this trend. In order to get a formula to quantify the increasing trend of the DiA, the simplest way is to assume the relationship between DiA and t to be linear, i.e. DiA=(0.571t/tc+1.487)×10-25. On this basis, the kinetic data of NGS of Bi in the de-segregation process are calculated (Curve IV in Fig. 3). It is seen that the calculated segregation level (i.e. Curve IV) is higher than the measured values. Therefore, the assumption of liner relationship is inappropriate.
According to Refs. [13,29,30], the relationship between Di and t is exponential. Therefore, the relationship can be formulated as
DiA=7.66×10at+bexp[-1.76/(kT)] (11)
Substituting the two simulated values of DiA (shown in Table 3) into Eq. (11), it can be obtained that a=8.45×10-8 and b=-13.37. For the real diffusion coefficient of Bi in Cu bicrystal, Di (shown in Table 1), the exponent parameter (at+b) is –5. It implies that when the annealing time t is 9.9×107 s (i.e. t>1146.5tc), DiA approaches Di of Bi in Cu bicrystal. On the basis of Eqs. (5) and (11), the kinetic data of NGS of Bi in the de-segregation process are calculated (Curve V in Fig. 3). It is seen that the calculated segregation level (i.e. Curve V) fits quite well with the measured values. Therefore, the exponential relationship is applicable.
3.3 Calculation of isochrone of NGS of Bi
Based on the NGS model, the GB segregation of solute atoms will reach the maximum at the critical time during isothermal annealing. A formula for the maximum solute GB concentration Cm(Ti+1) at annealing temperature Ti+1 after quenching from temperature Ti is given by [13,19]
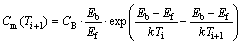 (12)
(12)
where Eb represents the vacancy–impurity binding energy. Substituting the parameters (Table 2) into Eq. (12), it is obtained that the values of Cm(Ti+1) fall between 0.01% and 0.07% (mole fraction) at holding temperatures between 400 and 650 °C. According to Section 3.2, the maximum content of Bi at GB at Ti is Cm(Ti)=3.67% (mole fraction). It is clear that the calculated values of Cm(Ti+1) are far less than those of Cm(Ti), which does not conform to the kinetic model of NGS. Therefore, Eq. (12) cannot effectively express the maximum solute content at the GB (Cm(Ti+1)). Up to the present, there is no reliable expression for the maximum content of NGS which can be used to predict the Cm(Ti+1) quantitatively. Thus, the isochronal kinetic data of Bi segregation are unable to be calculated. Further studies should be carried out to setup a reliable equation for the maximum content Cm(Ti+1) of NGS.
4 Conclusions
1) For the Cu bicrystals containing 0.005% Bi aging at 500 °C after quenching at solution temperature of 950 °C, the GB segregation of Bi is verified with EGS model and NGS model, respectively. It is concluded that both the isothermal kinetics and isochronal kinetics of Bi segregation agree well with the theory of NGS.
2) Some important parameters characterizing the NGS of Bi in Cu bicrystal are obtained: diffusion coefficient of Bi-vacancy complexes Dc=7.8×10-5×exp[-1.46/(kT)], apparent diffusion coefficient of Bi atoms DiA=7.66×10at+bexp[-1.76/(kT)], where a= 8.45×10-8, b =-13.37.
References
[1] XU Ting-dong. Critical time and temper embrittlement isotherms [J]. Materials Science and Technology, 1999, 15(6): 659-665.
[2] WU J, SONG S H, WENG L Q, XI T H, YUAN Z X. An Auger electron spectroscopy study of phosphorus and molybdenum grain boundary segregation in a 2.25Cr1Mo steel [J]. Materials Characterization, 2008, 59(3): 261-265.
[3] ZHENG Lei, ZHANG Mai-cang, DONG Jian-xin, MENG Ye. Relationship between grain boundary segregation of antimony and temper embrittlement in titanium-doped nickel-chromium steel [J]. Journal of Iron and Steel Research, 2011, 18(1): 68-72.
[4] SONG S H, WU J, WENG L Q, YUAN Z X. Fractographic changes caused by phosphorus grain boundary segregation for a low alloy structural steel [J]. Materials Science and Engineering A, 2008, 497(1): 524-527.
[5] XU T D, ZHENG L, WANG K, MISRA R D K. Unified mechanism of intergranular embrittlement based on non-equilibrium grain boundary segregation [J]. International Materials Reviews, 2013, 58(5): 263-295.
[6] ZHENG L, SCHMITZ G, MENG Y, CHELLALI R, SCHLESIGER R. Mechanism of intermediate temperature embrittlement of Ni and Ni-based superalloys [J]. Critical Reviews in Solid State and Materials Sciences, 2012, 37(3): 181-214.
[7] ZHENG L, CHELLALI R, SCHLESIGER R, BAITHER D, SCHMITZ G. Intermediate temperature embrittlement in high-purity Ni and binary Ni (Bi) alloy [J]. Scripta Materialia, 2011, 65(5): 428-431.
[8] ZHENG L, CHELLALI M R, SCHLESIGER R, MENG Y, BAITHER D, SCHMITZ G. Non-equilibrium grain-boundary segregation of Bi in binary Ni(Bi) alloy [J]. Scripta Materialia, 2013, 68(10): 825-828.
[9] SONG S H, WU J, YUAN Z X, WENG L Q, XI T H. Non-equilibrium grain boundary segregation of phosphorus under a high applied tensile stress in a 2.25Cr1Mo steel [J]. Materials Science and Engineering A, 2008, 486(1): 675-679.
[10] LI Wen-bin, PAN Qing-lin, XIAO Yan-ping, HE Yun-bin, LIU Xiao-yan. Microstructural evolution of ultra-high strength Al-Zn-Cu-Mg-Zr alloy containing Sc during homogenization [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(10): 2127-2133.
[11] OGURA T, MAKINO A, MASUMOTO T. A grain boundary etching method for the analysis of intergranular P-segregation in iron-based alloys [J]. Metallurgical Transactions A, 1984, 15(8): 1563-1570.
[12] CHEN Song-yi, CHEN Kang-hua, PENG Guo-sheng, LIANG Xin, CHEN Xue-hai. Effect of quenching rate on microstructure and stress corrosion cracking of 7085 aluminum alloy [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(1): 47-52.
[13] XU Ting-dong, CHENG Bu-yuan. Kinetics of non-equilibrium grain-boundary segregation [J]. Progress in Materials Science, 2004, 49(2): 109-208.
[14] FAULKNER R G. Segregation to boundaries and interfaces in solids [J]. International Materials Reviews, 1996, 41(5): 198-208.
[15] MCLEAN D. Grain boundaries in metals [M]. London: Oxford University Press, 1957.
[16] AUST K T, HANNEMAN R E, NIESSEN P, WESTBROOK J H. Solute induced hardening near grain boundaries in zone refined metals [J]. Acta Metallurgica, 1968, 16(3): 291-302.
[17] ANTHONY T R. Solute segregation in vacancy gradients generated by sintering and temperature changes [J]. Acta Metallurgica, 1969, 17(5): 603-609.
[18] FAULKNER R G. Non-equilibrium grain-boundary segregation in austenitic alloys [J]. Journal of Materials Science, 1981, 16(2): 373-383.
[19] XU Ting-dong, SONG Shen-hua. A kinetic model of non-equilibrium grain-boundary segregation [J]. Acta Metallurgica, 1989, 37(9): 2499-2506.
[20] FRACZKIEWICZ A, BISCONDI M. Intergranular segregation of bismuth in copper bicrystals [J]. Journal of Physics, 1985, 46: 497-503.
[21] XU T D, SONG S H, YUAN Z X. Equilibrium grain boundary segregation and the effect of boron in B-doped Fe-30wt%Ni austenitic alloy [J]. Acta Metall Mater, 1991, 39: 3199-3124.
[22] DIVINSKI S, LOHMANN M, HERZIG C. Grain boundary diffusion and segregation of Bi in Cu: Radiotracer measurements in B and C diffusion regimes [J]. Acta Materialia, 2004, 52(13): 3973-3982.
[23] BRAND E A, BROOK G B. Smithells metals reference book [M]. London: Butterworth, 1992.
[24] CHANG L S, RABKIN E, HOFMANN S, GUST W. Kinetic aspects of the grain boundary segregation in Cu (Bi) alloys [J]. Acta Materialia, 1999, 47(10): 2951-2959.
[25] ROTHMAN S J, PETERSON N L. Isotope effect and divacancies for self-diffusion in copper [J]. Physica Status Solidi, 1969, 35(1): 305-312.
[26] MEHRER H, SEEGER A. Interpretation of self-diffusion and vacancy properties in copper [J]. Physica Status Solidi, 1969, 35(1): 313-328.
[27] LAPORTE V, MORTENSEN A. Intermediate temperature embrittlement of copper alloys [J]. International Materials Reviews, 2009, 54(2): 94-116.
[28] ZHENG Lei, XU Ting-dong. Method for determining the elastic modulus at grain boundaries for polycrystalline materials [J]. Materials Science and Technology, 2004, 20(5): 605-609.
[29] XU Ting-dong. Kinetics of non-equilibrium grain-boundary segregation induced by applied tensile stress and its computer simulation [J]. Scripta Materialia, 2002, 46(11): 759-763.
[30] XU Ting-dong. Kinetic equations for non-equilibrium grain boundary segregation induced by applied tensile stress [J]. Materials Science and Technology, 2003, 19(3): 388-392.
[31] SMALLMAN R E. Modern physical metallurgy [M]. London: Butterworth, 1963.
杨武强1,徐 敏1,梁剑雄2,孟 晔1,郑 磊1
1. 北京科技大学 材料科学与工程学院,北京 100083;2. 钢铁研究总院 特殊钢研究所,北京 100081
摘 要:对Bi在Cu双晶中的晶界偏聚实验观察结果进行分析。利用平衡晶界偏聚(EGS)模型和非平衡晶界偏聚(NGS)模型,分别对500 °C时Bi在Cu双晶中的等温偏聚动力学和退火24 h的等时偏聚动力学进行研究。从定性分析和定量计算分析两方面推断出Bi的晶界偏聚特征与非平衡偏聚理论十分符合。根据非平衡晶界偏聚理论动力学模型,计算得到Bi-空位复合体扩散系数Dc=7.8×10-5exp[-1.46/(kT)],以及Bi原子的表观扩散系数DiA=7.66×10at+bexp[-1.76/(kT)],其中,a=8.45×10-8,b=-13.37。这些数据有助于对Cu合金中Bi所导致的脆化进行预测和控制的研究。
关键词:铋;铜;偏聚;晶界;扩散
(Edited by Wei-ping CHEN)
Foundation item: Project (51001011) supported by the National Natural Science Foundation of China; Project (141043) supported by the Fok Ying-Tong Education Foundation, China; Project (FRF-TP-12-042A) supported by the Fundamental Research Funds for the Central Universities, China
Corresponding author: Lei ZHENG; Tel: +86-10-62332884; E-mail: zhenglei_ustb@sina.com
DOI: 10.1016/S1003-6326(14)63566-4

