文章编号：1004-0609(2012)03-0948-06

线性EIV模型的TLS估计及其典型应用

周拥军^{1, 2}，邓才华^{1, 2}

(1. 中南大学 有色金属成矿预测教育部重点实验室 长沙 410083；

2. 中南大学 地球科学与信息物理学院，长沙 410083)

摘  要：推导了将线性GM模型转换为变量含误差(EIV)模型并采用总体最小二乘(TLS)平差的方法，介绍了加权总体最小二乘、混合总体最小二乘和附限制条件的总体最小二乘问题及其解算方法。以经典大地测量控制网平差和数据拟合算例比较各种TLS估计的精度和计算效益。理论分析和算例表明：对于EIV模型，WTLS为最优估计，实际应用时需根据具体函数模型和随机假设选择合理的TLS平差方法。

关键词：线性EIV模型；GM模型；测量平差；总体最小二乘

中图分类号：P207　　     文献标志码：A

Extended total least squares problems for linear errors-in-variables model and its typical applications

ZHOU Yong-jun^{1, 2}, DENG Cai-hua^{1, 2}

(1. Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education, Changsha 410083, China;

2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)

Abstract: The method of converting linear Gauss-Markov (GM) model to linear errors-in-variables (EIV) model was given, an ordinary total least squares (TLS) adjustment algorithm were introduced as an alternative method for converted EIV model. Extended TLS methods of weight TLS, mixed ordinary LS and TLS, constrained TLS estimators with computational schemes were introduced as well. A typical geodetic control network adjustment and a curve fitting data experiments are given to compare the adjustment results in accuracy and computation efficiency by TLS and traditional LS methods. The data experiments and theoretic analysis indicate that WTLS method is an optimal estimator for EIV model, reasonable TLS algorithms should be selected according to the function model and associated stochastic model in practical application.

Key words: linear error in variables (EIV) model; Gauss-Markov (GM) model; least squares adjustment; total least squares

现代测量平差与数据处理理论是以高斯-马尔柯夫(Gauss-Markov, GM)模型为核心，通过该模型在不同层面上的拓展形成的若干新理论、新方法^[1-2]。GM模型仅考虑观测值的误差，而认为系数矩阵没有误差，而在实际应用中，大多数情况下系数矩阵是有误差的。EIV模型是指观测值和参数均包含误差的模型，针对线性EIV模型，GOLUB等^[3]最早提出了总体最小二乘估计方法，MARKOVSKY等^[4-5]对扩展TLS问题 及其算法进行了深入的研究，SCHAFFRIN等^[6-9]和NEITZEl^[10]将TLS估计引入到测量数据处理中，国内测绘领域的学者也从理论、应用等方面对TLS进行了深入研究^[11-14]。但TLS用于解算线性GM模型和EIV模型估计方法的差异，各种扩展TLS模型解算具体问题的差别等尚未有深入的研究。

为方便总体最小二乘方法在测量数据处理中的应用，这里将系数矩阵的误差分为两类，一类是线性化造成的设计矩阵元素的误差，经典GM模型大多是非线性的观测方程在取参数近似值后得到的线性方程，参数初值对系数矩阵的取值有直接影响，这时系数矩阵包含的不仅仅是误差而是包含模型误差，这类问题在大多数需要线性化的测量平差问题中大量存在，而且需要迭代计算。另一类是设计矩阵元素是只包含观测值，如线性回归、直接线性变换、曲线拟合等，很显然设计矩阵含有误差。本文作者比较了GM模型与线性EIV模型和估计方法的区别，并给出了两类问题的算例，旨在推广TLS估计在测量数据处理中的应用。

1  线性EIV模型与GM模型的比较

测量平差领域常用的线性GM模型可表示为

                   (1)

式中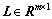：表示观测值向量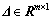，表示观测值向量的真误差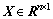，表示待估参数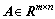，表示系数矩阵，其中m、n分别表示观测值和未知参数的个数，且满足m≥n。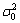表示单位权方差，P表示观测值的权矩阵。经典测量平差问题是以最小二乘准则为代价函数的参数估计，可以证明最小二乘准则和最大似然准则是一致的，具有无偏，方差最小等统计特征。

线性EIV(Errors-in-variables)模型除了考虑观测值的误差外，还考虑矩阵A的误差，其数学模型可表示为

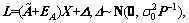
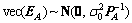                    (2)

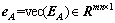式中：E_A表示观测矩阵A的误差向量，表示系数矩阵的真值，表示矩阵E_A按列向量化后得到的向量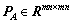，表示e_A的权阵。对于线性EIV模型应采用总体最小二乘估计，文献[3]中已证明总体最小二乘估计是EIV模型的最大似然估计，其目标函数可表示为

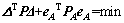                         (3)

为简化表达，先假设所有误差服从独立、等方差的正态分布，则权矩阵为单位矩阵，式(3)可表示为

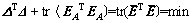              (4)

式中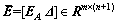：表示误差增广矩阵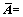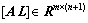， 表示系数增广矩阵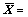，[X; -1] R^(n+1)×1表示增广参数向量，因此，式(2)改写为

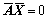                                    (5)

很显然，式(5)有无穷多个解，为得到唯一解，可设定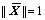作为参数的约束条件，因此总体最小二乘模型等价于：

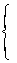
                              (6)

引入Eckart-Young-Mirsky矩阵近似定理：矩阵AR^m×n，其秩rank(A)=r的svd分解可表示为A=

UΣV^T=，其中，σ_i为矩阵A的奇异值，U、

V为正交矩阵，其向量形式为，，u_j和v_j分别为矩阵A的奇异值

σ_j对应的左、右向量。若k≤r，，并存

在以下关系：

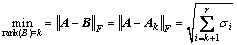        (7)

若不考虑参数之间的约束则rank(A)=n，即系数矩阵列满秩，欲使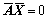有非零解，则必有rank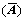＜  n+1，根据Eckart-Young-Mirsky矩阵近似定理，取rank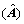=n作为原矩阵的近似，则有：

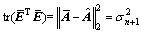                      (8)

并得到待求参数为

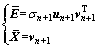                            (9)

以上推导表明，经典GM模型可以扩展如式(6)所示的线性EIV模型，其对应的估计方法也由传统的LS估计方法变为TLS估计，对应的扩展参数解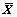的解为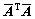经奇异值分解后得到的最小特征值所对应的右特征向量v_n+1，由于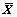=[X, -1]，从而得到参数的估计值为

                 (10)

可以证明，它与常规的法方程求逆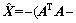 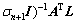的估计结果是一致的，很显然直接分解方法更简洁，得到参数的估计值后可进一步得到的单位权方差：

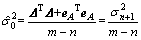                     (11)

2  TLS估计的扩展

2.1  WTLS问题

通过上面的分析可知，经典GM模型可以方便地扩展为线性EIV模型，但目前诸多应用并未考虑设计矩阵的权，所得到的总体二乘结果并非满足统计上的最优。欲确定权阵，首先要确定A的协方差阵C(A)，则C(A)R^mn×nm，若用表示A的真值，令A=+E_A，根据协方差阵的定义：

C(A)=E[(E_A)_ij(E_A)_kl]                          (12)

式中：i，j，k，l表示对应的矩阵元素。若考虑协方差阵的一般形式，势必增加计算的工作量，MARKOVSKY等^[4-5]根据不同的应用实例对方差阵进行了简化，若矩阵A按行独立，且每行具有相同的方差阵，则这类问题称为广义总体最小二乘问题(GTLS)。若矩阵A按行独立，但各行的方差阵不同，则称为按行的加权总体最小二乘问题(Row-wise weighted total least-squares problem，RWTLS)。根据权阵的结构，可以将加权总体最小二乘问题表示为表1的形式，除广义最小二乘可以采用类似简单TLS问题的直接分解算法外，其它的WTLS均需要迭代^[4]。

测量平差中的GM模型，系数矩阵A是独立的观测方程经线性化得到的，即：

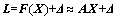                         (13)

式中：

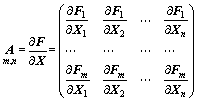            (14)

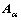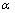由于观测值间相互独立，矩阵A的各行相互独立，但每行的元素是相关的，因此属于Row-wise WTLS问题，用表示A的第行(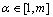)，其对应的方差阵如下：

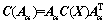                          (15)

C(X)表示未知参数的方差阵由下式确定：

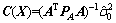                         (16)

从而得到扩展参数的方差阵为，进而简单总体最小二乘问题变换为加权最小二乘问题：

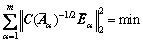                     (17)

TLS可以通过奇异值分解算法实现，而WTLS由于权阵与参数相关，需要迭代求解，具体的计算步骤如下^[4]：

1) 根据给定的参数初值列出误差方程；

2) 给定权阵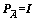按简单TLS方法得到参数初值；

3) 根据误差传播率得到参数的方差阵C(X)，并逐行得到各元素的方差阵；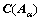

4) 根据加权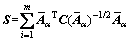，则解为将S进行SVD分解后最小特征值所对应的特征向量；

5) 将得到的参数与初值比较，如果小于某一阈值，则计算完成，否则回到式(3)进行迭代计算。

2.2  混合OLS-TLS问题

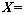
测量中的权矩阵为方差阵的逆矩阵，而系数矩阵A的某些元素可能为常数，因此这些项对应的方差分量为零，从而导致无法通过方差阵求逆得到权阵，此时需要采用混合最小二乘方法求解，这里先不考虑A的权，令A=[A₁, A₂]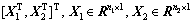，，， ，将式(1)变为

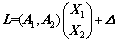                         (18)

式中：系数矩阵A₁无误差，而A₂含有误差，则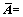 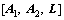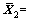，，[X₂, -1]，将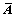进行QR分解，得到：

                       (19)

表1  权阵的结构及对应的总体最小二乘问题

Table 1  Weighted matrix structure and its corresponding TLS problems

可以根据解出X₂，然后回代到方程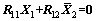中，解出X₁的值，然后根据前面的方法进行精度评定。

2.3  CTLS问题

这里仅考虑线性约束条件，至于非线性约束条件可以根据参数初值线性化后得到线性约束条件，线性条件一般可表达为

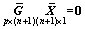                             (20)

CTLS问题可以采用迭代解法^[4]或直接分解算  法^[15]，具体的解算过程本文不再列出。

3  算例

选择两个典型算例，一个是典型的大地测量控制网平差，需要给定参数初值转化为误差方程，然后根据间接平差法求解(以下简称LS估计)，然后将误差方程拓展为线性EIV模型，用TLS方法求解，并比较二者在参数初值、迭代次数、估计精度等的差别；二是曲线拟合的算例，其设计矩阵有误差，但不受参数初值的影响，比较分析各种估计方法。

3.1  测量控制网平差算例

图1所示为一测角网，A、B、C 3点的坐标分别为(8 864.530，5 392.580)、(13 615.220，10 189.470)、(6 520.120、14 399.300)，观测数据见表1。为了比较初值对估计结果的影响，选择了两组初值，分别采用经典最小二乘方法、总体最小二乘方法和加权总体最

小二乘方法进行迭代计算，取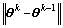＜10^-6作为

迭代终止条件，计算的结果见表3。计算结果表明：当初值接近估计值时，3种方法的迭代次数和最终估值基本相等，而经典大地测量网的初值往往与估值较接近，说明迭代LS估计和TLS估计在计算速度和精度上并无明显改进。若初值偏离估值较远，迭代TLS估计要略快于LS估计的收敛速度，在估计结果上也仅有微小差异，说明初值和估计方法对结果影响不大。但需要指出的是，简单TLS在设计矩阵的所有元素都满足独立等精度分布的前提下才是最优估计^[4]，而这一随机假设在实际问题中基本不成立，导致简单TLS估计多为有偏估计。当函数模型较复杂、设计矩阵病态时，TLS估计和LS估计的结果就会有较大差异，故简单TLS仅适用于近似平差计算。在严密平差时，需采用WTLS方法或经典平差方法，但WTLS方法需要根据观测值的误差传播率得到设计矩阵元素的方差，以设计矩阵元素的最小二乘准则为目标函数进行平差计算，这导致计算较间接平差方法复杂，因此，经典控制网平差从计算效率和精度而言并不适宜采用WTLS方法。

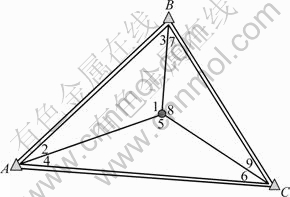
图1  某大地测量控制网

Fig. 1  A typical geodetic control network

3.2  曲线拟合算例

便于和为真值比较，这里采用模拟算例，设二次曲线的方程为y=ax²+bx+c，参数真值分别为：3、5、10，取x为 [0,10]区间内产生的10个随机数，并按以上方程得到y的值，然后在x和y上均叠加方差为0.01的正态分布误差，分别用LS、TLS、OLS-TLS、WTLS估计参数，做10 000次模拟实验，然后比较各种估计

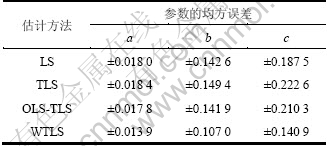
方法的均方误差，得到的计算

结果见表4，表明TLS和OLS-TLS的计算效果甚至  比LS还差，主要原因是TLS虽然考虑了设计矩阵的误差，但假设矩阵各元素的误差是独立等精度分布 的，而本实例中各元素的误差明显不相等，因此造成了TLS估计效果不理想，而WTLS由于考虑了各元  素的统计特性，因而估计效果最佳。作者还采用变换各参数数量级的方法来模拟，发现简单TLS和LS方法各有优劣，但WTLS的估计效果仍为最佳，由于篇幅原因在此不再列出。

表2  观测数据

Table 2  Observed data

表3  平差结果

Table 3  Results estimated by LS, TLS and WTLS

表4  LS、TLS、OLS-TLS和WTLS方法的参数均方误差比较

Table 4  Roots of mean square estimated by LS, TLS, OLS-TLS and WTLS

4  结论和建议

1) 线性GM模型能方便地转换为线性EIV模型并用TLS方法求解。

2) 对于线性EIV模型，简单TLS估计仅在设计矩阵元素服从独立等方差分布时才是最优估计，因此，简单TLS方法的估计精度不一定优于LS方法的估计精度，简单TLS估计一般适用于近似平差计算。

3) 对于不等精度观测值问题，若要获取高精度的平差结果，宜采用WTLS方法。虽然经典控制网平差的函数模型可经线性化得到线性GM模型，而后转换为EIV模型并采用WTLS平差方法得到与经典方法精度相当的平差结果，但计算过程较间接平差复杂，因此建议仍采用经典间接平差方法。而对于曲线拟合等以坐标为观测值的平差问题，采用WTLS估计相对简便，本文作者将做进一步的研究。

REFERENCES

[1] 朱建军, 宋迎春. 现代测量平差与数据处理理论的进展[J]. 工程勘察, 2009, 37(12): 1-5.
ZHU Jian-jun, SONG Ying-chun. Progress of modern surveying adjustment and theory of data processing [J]. Geotechnical Investigation & Surveying, 2009, 37(12): 1-5.

[2] 欧阳文森, 朱建军. 经典平差模型的扩展[J]. 测绘学报, 2009, 38(1): 12-15.
OUYANG Wen-sen, ZHU Jian-jun. Expanding of classical surveying adjustment model [J]. Acta Geodaeticaet Cartographic Sinica, 2009, 38(1): 12-15.

[3] Golub G H, VAN LOAN C F. An analysis of the total least squares problem [J]. SIAM J Numer Anal, 1980, 17: 883-893.

[4] Markovsky I, Van Huffel S. Overview of total least squares methods [J]. Signal Process, 2007, 87(10): 2283-2302.

[5] Markovsky I, Rastello M L, Premoli P, KUKUSIT A, van HUFFEL S. The element-wise weighted total least squares problem [J]. Computational Statistics & Data Analysis, 2006, 50(1): 181-209.

[6] Schaffrin B, Felus Y A. On total least-squares adjustment with constraints [C]// Windows on the Future of Geodesy, IAG-Symp. Springer, Berlin, 2005, 128: 417-421.

[7] Schaffrin B. A note on constrained total least squares estimation [J]. Linear Algebra Application, 2006, 417(1): 245- 258.

[8] Schaffrin B, WIESER A. On weighted total least-squares adjustment for linear regression [J]. Journal of Geodesy, 2008, 82(6): 373-383.

[9] SCHAFFRIN B, Felus Y A. On the multivariate total least-squares approach to empirical coordinate transformations—Three algorithms [J]. Journal of Geodesy, 2008, 82(6): 373-383.

[10] NEITZEL F. Generalization of total least-squares on example of unweighted and weighted 2D similarity transformation [J]. Journal of Geodesy, 2010, 84(12): 373-383.

[11] 鲁铁定, 陶本藻, 周世健. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报: 信息科学版, 2008, 33(5): 504-507.
LU Tie-ding, TAO Ben-zao, ZHOU Shi-jian. Modeling and algorithm of linear regression based on total least squares [J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 504-507.

[12] 陆 珏, 陈 义, 郑 波. 总体最小二乘方法在三维坐标转换中的应用[J]. 大地测量与地球动力学, 2008, 28(5): 77-81.
LU Jue, CHEN Yi, ZHENG Bo. Applying total least squares to three dimensional datum transformation [J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 77-81.

[13] 袁振超, 沈云中, 周泽波. 病态总体最小二乘模型的正则化算法[J]. 大地测量与地球动力学, 2009, 29(2): 131-134.
YUAN Zhen-chao, SHEN Yun-zhong, ZHOU Ze-bo. Regularized total least-squares solution to ill-posed error-in- variable model [J]. Journal of Geodesy and Geodynamics, 2009, 29(2): 131-134.

[14] 孔 建, 姚宜斌, 吴 寒. 整体最小二乘的迭代解法[J]. 武汉大学学报: 信息科学版, 2010, 35(6): 711-714.
KONG Jian, YAO Yi-bin, WU Han. Iterative method for total least-squares [J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 711-714.

[15] DOWLING E M, DEGROAT R D, LINEBARGER D A. Total least squares with linear constraints [C]// IEEE, International Conference on Acoustics, Speech, and Signal Processing, 1992: 341-347.

(编辑 何学锋)

基金项目：国家自然科学基金资助项目(40974007)；中国博士后基金资助项目(20100480948)；中南大学博士后基金资助项目

收稿日期：2011-12-01；修订日期：2012-02-20

通信作者：周拥军，博士；电话：0731-88879330；E-mail: yjzhou2009@hotmail.com