基于Oracle Spatial的地籍地块空间拓扑关系判断

 周晓光^1,2,岳国森¹,魏金占¹,赵仁亮³,朱建军¹,向南平¹

(1.中南大学 信息物理工程学院,湖南 长沙,410083;
2.辽宁工程技术大学 地理空间信息技术与应用实验室,辽宁 阜新,123000;
3.国家基础地理信息中心,北京,100044)

摘要: 将地籍地块间空间拓扑关系的判断分为2个层次来处理:2个简单地块间空间拓扑关系的判断;1个简单地块与1个复合地块间空间拓扑关系的判断。2个简单地块间空间拓扑关系的判断可直接利用Oracle Spatial提供的空间关系查询操作算子来实现;复合地块和简单地块间空间拓扑关系的判断,按照双四元交模型(D4I)的思想,将其转化为2组简单地块,然后利用Oracle Spatial的空间关系查询操作算子来处理。研究结果表明:在Oracle Spatial平台上实现了地籍地块间31种空间拓扑关系(包括2个简单地块间的8种空间拓扑关系和1个简单地块与1个复合地块间的23种空间拓扑关系)的判断,并且这种判断方法同样适用于其他类型二维面域或复杂目标间空间拓扑关系的判断。
关键词: 地籍地块; Oracle Spatial; 空间拓扑关系; 双四元交模型; 操作算子
中图分类号:P208 文献标识码:A 文章编号: 1672-7207(2005)02-0317-06

A Computation Method of Parcels′ Topological Relations Based on Oracle Spatial

ZHOU Xiao-guang^1,2,YUE Guo-sen¹,WEI Jin-zhan¹,
ZHAO Ren-liang³,ZHU Jian-jun¹,XIANG Nan-ping¹

(1.School of Info-physics and Geomatics Engineering, Central South University, Changsha 410083, China;
2.Geomatics and Applications Laboratory, Liaoning Technical University, Fuxin 123000, China;
3.National Geomatics Center of China, Beijing 100044, China)

Abstract: A computation method of the topological relation between parcels was developed based on Oracle Spatial. In this paper, 31 kinds of topological relations between parcels are firstly distinguished according to D4I model, which includes 8 kinds of relations between two simple parcels, and 23 kinds of relations between a parcel with one hole and a simple parcel. Then the computation method of the topological relations was presented, the relations between simple parcels was ascertained directly by the query operators that Oracle Spatial supported. The results show that the relations between a parcel with one hole and a simple parcel can not be ascertained directly, and the parcel with one hole is divided into two simple parcels according to D4I model. Such kinds of relations can be ascertained by the relations of 2 pairs of simple parcels, which can be ascertained directly. In addition, a topological relations computation method between parcels is developed in this paper, which can determine 31 kinds of topological relations between two parcels. This method can be used to the topological relations computation of other regions and other composite entities in 2-dimension euclidean space.
Key words: parcel; Oracle Spatial; spatial topological relation; D4I model; operator
   地籍的核心是地块,地块间存在着多种空间关系,这些关系在地籍信息查询、分析和地籍数据更新时起着重要作用。地籍地块间空间拓扑关系问题可分为3个方面:地籍地块间空间拓扑关系的描述与区分;地籍地块间空间拓扑关系的数据组织;地籍地块间空间拓扑关系的判断与查询^[1,2]。地块可看作二维(IR²)欧氏空间中的一个面域^[1],一般来说,人们采用两面域之间的交集来描述它们之间的空间拓扑关系^[3]。目前,空间拓扑关系的描述方法主要有:M.EGENHOFER等根据点集拓扑理论建立的四元组模型(4-intersection model)和九元组模型(9-intersection model)等基本方法^[4,5];CHEN Jun等提出的基于Voronoi图的V9I模型等改进方法^[6];LI Zhi-lin等提出的使用空间目标的整体及其Voronoi 区域,应用基本的集合算子进行空间关系计算的VW 方法等^[7,8]。但上述方法都没有区分甚至不能区分在地籍信息系统中比较常见的1个简单地块和1个复合地块(即1个大地块中包含1个小地块的地块)之间的空间拓扑关系类型。M.EGENHOFER等在四交模型基础上提出了一个包含空洞的两面域间空间拓扑关系的描述框架^[9],但是这一描述框架过于复杂,并且没有描述任意复杂程度空间目标之间的拓扑关系类型。目前,某些大型的数据库系统(如Oracle Spatial)已经提供了四元组和九元组模型空间拓扑关系操作的基本算子^[10]。但是,四元组和九元组模型存在线性相关性(内部与外部线性相关性),在目标维数与背景空间维数不等的情况下存在拓扑定义不一致性、外部无限性、难以操作等理论缺陷^[7,8]。在地籍信息系统中,由于地籍地块的目标维数与背景维数都为2,四元组模型与九元组模型仍然适用,并且在这种情况下,四元组模型与九元组模型等价。由于四元组模型相对简单,因此,周晓光等在其基础上提出了一种地籍地块空间拓扑关系描述的双四元交模型(简称D4I模型)^[1],并推导了地块间常见的31种空间拓扑关系。这些空间拓扑关系的描述与澄清利于地籍信息查询、分析和地籍数据更新。目前,许多大型的GIS应用系统采用Oracle数据库作为其空间数据管理的基础平台。Oracle数据库是一种大型的对象-关系型数据库,Oracle Spatial是Oracle公司提供的一种不需要中间接口而直接使用数据库操作系统来存储和管理空间数据的空间数据插件,它提供了四元组模型和九元组模型描述的8中基本空间拓扑关系查询操作算子:DISJOINT(边界和内部均不相交),TOUCH(仅边界相交),OVERLAPBDYINTERSECT(边界和内部相交),EQUAL(相等),CONTAINS(包含),COVERS(包含且边界相交),INSIDE(CONTAINS的逆)和COVEREDBY(COVERS的逆)。但是不能直接利用这些操作算子来判断地籍地块间常见的其余23种空间拓扑关系。为此,作者利用Oracle Spatial提供的空间关系操作算子,并根据D4I模型对复合地块与简单地块间空间拓扑关系的定义,提出实现D4I模型描述的31种地块间空间拓扑关系的判断方法,并对其进行实验验证。

1 地籍地块间的空间拓扑关系

1.1 简单地块间的空间拓扑关系

简单地块可看作二维(IR²)欧氏空间中的一个简单面域。一般认为二维(IR²)欧氏空间中的两个简单面域间包括DISJOINT,INSIDE,EQUAL,MEET,COVEREDBY,CONTAINS,COVER和OVERLAP 8种基本拓扑关系(详情参见文献[5]图3),分别对应于ORACLE SPATIAL 的DISJOINT,INSIDE,EQUAL,TOUCH,COVEREDBY,CONTAINS,COVERS,OVERLAPBDYINTERSECT 8个操作算子。
1.2 简单地块和复合地块间的空间拓扑关系

在双四元交模型中,复合地块A的空洞H^A被定义为A的一个严格包含于A中的内部连通且具有连续边界的非空集合,且H^A与A的外边界不相接;复合地块A的总区域A^*为A及其空洞的并集,即:A^*=A∪H^A,且A^*为简单面域。因此,复合地块A与简单地块B间的空间拓扑关系的描述可转化为A的总区域A^*和A的空洞H^A与简单地块B间的关系,然后用简单地块间的8种空间拓扑关系的组合来描述。若将复合地块A拆分为外多边形和内多边形,则总区域A^*可以用A的外多边形表示,空洞H^A可以用A的内多边形表示,如图1所示。

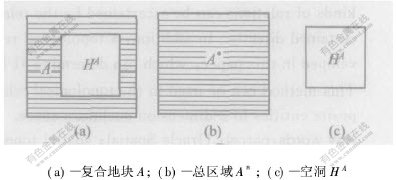
图 1   复合地块A及其总区域A^*与空洞H^A
Fig. 1   Definition of a parcel with one hole,its whole region A^* and hole H^A

双四元交模型共描述了23种简单地块和复合地块间的空间拓扑关系类型,各种关系及其描述见文献[1]。

2 简单地块间空间拓扑关系的判断

简单地块间的8种空间拓扑关系可以直接通过Oracle Spatial提供的空间关系操作运算符SDO_RELATE(需要空间数据索引) 和函数SDO_GEOM.RELATE()(不需要空间数据索引)对存储在数据库表中地理实体列的实体进行运算来实现。

Oracle Spatial采用对象关系模式将所有地理实体的属性数据和图形数据存储在同一张数据库表中,每一条记录存储一个地理实体,各地理实体间具有独立性,不存在任何依赖关系。它定义了一种新的数据类型即SDO_GEOMETRY空间对象类型来存储地理实体的图形数据,并和地理实体的属性数据一起存放为数据库表的一条记录。如表1中的GEOLOC列存放地块的图形数据,其他列则存放地块的属性数据。地块间空间拓扑关系的判断主要通过空间数据操作运算符或者空间函数针对GEOLOC列进行操作来实现。

表1所示为用MapInfo的Easyloader7.0上载地图数据到Oracle数据库后的结构。SDO_GEOM.RELATE()函数的参数形式如下: SDO_GEOM.RELATE(Geometry1,′mask′,Geometry2,tol)。

其中,Geometry1和Geometry2是表1中的GEOLOC列存储的几何对象(Geometry Object);mask表示查询的参数,它定义查询的拓扑关系类型,当为“determine”时,该函数必须在select关键字之后,查询的是2个实体间的拓扑关系;当为其他具体代表拓扑关系的关键字时,必须和where 子句一起使用;tol表示查询时指定的误差。下面结合实例说明使用SDO_GEOM.RELATE()函数对简单地块间拓扑关系判断的程序实现。

表 1   Oracle Spatial的数据库表结构
Table 1   Datum table structure in Oracle Spatial

地块间有意义的空间拓扑关系查询分为2种:一种是查询2个地块间的空间拓扑关系,另一种是查询与某个地块具有某种指定拓扑关系的所有地块。

对于第1种查询,可以在select语句的where子句中设定2个地块的判定条件,以提高系统的执行效率,节约运行时间。在VC中利用OO4O连接Oracle数据库后,可用下列函数来实现2个简单地块间拓扑关系的判断:

bool CTabView: Relation(Cstring tablename1, Cstring tablename2) CString idObjB, CString idObjA, CString &result)

 // idObjB, idObjA分别表示B和A地块的ID号,result返回两地块间的拓扑关系。

{

CString query;

query.Format("select MDSYS.SDO_GEOM.RELATE(a.geoloc,'DETERMINE',b.geoloc, 0.0001) from %s b,%s a where b.ID=%s and a.ID=%s ",tablename1,tablename2, idObjB, idObjA);

ODynaset odyn(odb,query);

//odb为ODatabase对象

if(!odyn.IsOpen())

{ AfxMessageBox(odb.GetErrorText());

 AfxMessageBox(odyn.GetErrorText());

 return false;

}

try

{

 while(!odyn.IsEOF())

 {

  char aa[15];

  odyn.GetFieldValue(0,aa,15);

  result.Format("%s",aa);

  odyn.MoveNext();

 }

}

catch(OException E)

{

 CString error;

 error.Format("错误:%s, %s",

E.GetFailedMethodName(),E.GetErrorText())

 MessageBox(error);

}

return true;

}

由于where子句中设定2个物体的ID值做判定条件,因此,函数查询的结果只能是这2个ID值所指定的地块间的关系。2个简单地块间的拓扑关系是惟一的,因此,结果集中所包含的关系值的个数只能是1。由于在查询时SDO_GEOM.RELATE()函数指定的是“DETERMINE”关键字,因此,查询的结果应该是“A地块 result B地块”。对于面状地物,使用“DETERMINE”关键字执行的结果,即“result”的值,只能是Oracle Spatial定义的8种空间拓扑关系之一,即只能是DISJOINT,TOUCH,OVERLAPBDYINTERSECT,EQUAL,CONTAINS,COVERS,INSIDE或者COVEREDBY。如当A和B两地块间的关系是“DISJOINT”时,则 “result”的值为“DISJOINT”; 当A和B两地块间的关系是“OVERLAPBDYINTERSET”时,则“result”的值为“OVERLAPBDYINTERSET”。其他关系依此类推。

此外,SDO_GEOM.RELATE()函数要求指定A和B两地块查询时的误差,这里指定的是“0.0001”。实际应用中可以根据需要指定不同的误差。

对于第2种查询,其原理与第1种相似,不同的是对整个表中的所有数据行依次进行运算(通常不采用)或者对某一选择范围内的实体进行判断。如查询“TOUCH”某一地块的所有地块的ID号时,查询语句为:

query.Format("select a.ID from %s b,%s a where b.ID=%s and MDSYS.SDO_RELATE(a.geoloc, 'TOUCH',b.geoloc,0.0001)= 'TRUE'",tablename1, tablename2, idObj);

一般来说,Oracle Spatial中存储的地块记录数量很大,为提高检索的速度,可以利用其提供的过滤(FILTER)和求精(RELATE)技术,即在进行地块拓扑关系判断运算时,先利用SDO_FILTER技术,对地块的最小外包矩形进行计算,求出可能具有该种拓扑关系的所有地块集合,然后再对该集合进行求精运算,即使用SDO_GEOM.RELATE()函数精确判定拓扑关系,获得最终结果。

3 复合地块与简单地块间空间拓扑关系判断的实现

利用Oracle Spatial虽然能直接区分出简单地块之间的空间拓扑关系,但是却不能区分带有空洞的复合地块之间的拓扑关系,因此,可以考虑将这种关系转换为简单地块间的拓扑关系,从而利用其空间操作进行判断。

在Oracle Spatial中,SDO_GEOMETRY空间对象类型既是存储点、线、多边形的容器,也是存储它们的同类或异类积聚体的容器。复合地块被看作是多边形的同类积聚体进行存储。在存储时,首先进入复合地块的外多边形,按照坐标对的逆时针顺序存储,然后进入其内多边形,按照坐标对的顺时针顺序存储,并且外多边形和内多边形必须相离(DISJOINT)。图2所示复合地块的存储形式如下:

图 2   带空洞地块的存储说明
Fig. 2   Storage illumination of a parcel with one hole [TS)]

MDSYS.SDO_GEOMETRY(

2003, //表示二维多边形

262148, //表示坐标系

NULL, //点信息

MDSYS.SDO_ELEM_INFO_ARRAY(1,1003,1,15,2003,1), //对存储几何目标的坐标说明

MDSYS.SDO_ORDINATE_ARRAY(10,10,12,6,19,6,20,15,15,18,10,16,10,10,13,8,12,12,16,14,15,8,13,8) //存储多边形的各顶点坐标对

)

在MDSYS.SDO_ELEM_INFO_ARRAY(1,1003,1,15,2003,1)中,1003表示元素是外多边形,2003表示元素是内多边形,15表示对第2个元素(内多边形)的坐标的定义起始于MDSYS.SDO_ORDINATE_ARRAY所存储的复合多边形的所有顶点坐标中的第15个元素(这里第15个元素是13,因此,内多边形的第1个顶点的坐标对是(13,8))。按照Oracle Spatial对含有空洞区域的存储方法,图2中的复合地块可以拆分为2个简单地块:外多边形所构成的简单地块(即A^*)和内多边形所构成的简单地块(即H^A)。其SDO_GEOMETRY的类型信息如下。

a. 外多边形:

MDSYS.SDO_GEOMETRY(

2003,

262148,

NULL,

MDSYS.SDO_ELEM_INFO_ARRAY(1,1003,1),

MDSYS.SDO_ORDINATE_ARRAY(10,10,12,6,19,6,20,15,15,18,10,16,10,10))

b. 内多边形:

MDSYS.SDO_GEOMETRY(

2003,

262148,

NULL,

MDSYS.SDO_ELEM_INFO_ARRAY(1,1003,1),

MDSYS.SDO_ORDINATE_ARRAY(13,8,15,8,16,14,12,12,13,8))

在判断简单地块与复合地块间的空间拓扑关系时,可转化为判断简单地块与该复合地块的总区域(即其外多边形所构成的简单地块)间的关系和简单地块与该复合地块的空洞(即其内多边形所构成的简单地块)间的关系。程序的实现原理与上相同,所不同的是需对查询语句稍做修改。如判断简单地块与复合地块内多边形的拓扑关系时,查询语句如下:

strQuery.Format("select MDSYS.SDO_GEOM.RELATE(a.geoloc, 'DETERMINE', MDSYS.SDO_GEOMETRY(2003,262148,NULL,

MDSYS.SDO_ELEM_INFO_ARRAY(1,1003,1),

MDSYS.SDO_ORDINATE_ARRAY(13,8,15,8,16,14,12,12,13,8))) from %s a where a.ID=%s and”, tablename, idObj);

4 实验验证

应用程序集成VC++6.0与MapInfo7.0,实现对Oracle空间数据的显示;用OO4O(Oracle Object for OLE)访问Oracle Spatial空间数据,通过返回在地图窗口所选择地块的惟一ID标识号,实现判断地块间的空间拓扑关系。对D4I模型描述的31种地块拓扑关系(包括8种简单地块间的拓扑关系和23种复合地块与简单地块间的空间拓扑关系)都进行了实验验证,实验证明该方法能够判断复合地块和简单地块间的空间拓扑关系。图3所示为其中的一种情况。

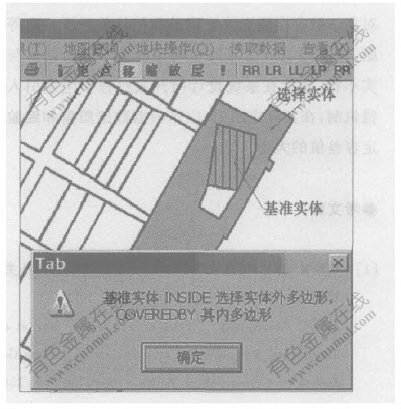
图 3   复合地块与简单地块的空间拓扑关系判断
Fig. 3   Judgment of topological relation between a parcel with one hole and a simple parcel

图3所示为查询1个包含空洞的复合地块和1个简单地块间空间拓扑关系的输出结果,其中简单地块“COVEREDBY”复合地块的空洞。程序输出结果为“基准实体 INSIDE 选择实体外多边形,COVEREDBY其内多边形”。其中,“基准实体”为简单地块,复合地块为“选择实体”,内多边形指复合地块的空洞。

5 结 语

a. 2个简单地块间的空间拓扑关系判断可直接通过Oracle Spatial提供的拓扑关系操作算子来实现;

b. 复合地块与简单地块间的空间拓扑关系判断可通过判断简单地块与该复合地块的总区域和简单地块与该复合地块的空洞地块之间的空间拓扑关系来实现;

c. 所提出的实现方法同样适用于其他类型二维面域间的空间拓扑关系判断及其他复杂对象间空间拓扑关系的判断。

d. 由于空间数据库数据质量的影响,如数据库对象一般存在图形位置误差和拓扑关系不一致等问题,这些问题可能导致空间拓扑关系判断结果与现实不符,因此在系统设计与开发过程中应该引入容错机制,在实际应用中,应该根据数据质量和经验选定容差值的大小。

参考文献:

[1]周晓光,陈军,蒋捷,等.地籍地块间空间拓扑关系描述[J].测绘学报,2003,32(4):356-361.
ZHOU Xiao-guang, CHEN Jun, JIANG Jie, et al. Topological Relations Between Parcels[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4):356-361.
[2]常征,陈军.顾及地块时空特点的地籍数据组织及查询[J].武汉测绘科技大学学报,1997,22(3): 216-221.
CHANG Zheng, CHEN Jun. Spatio-temporal Data Organization and Querying of Cadastral Information System [J]. Journal of Wuhan Technical University of Surveying and Mapping, 1997,22(3): 216-221.
[3]陈军,赵仁亮.GIS空间关系的基本问题与研究进展[J].测绘学报,1999,28(2):95-102.
CHEN JUN, ZHAO Ren-liang. Spatial Relations in GIS: A Survey on Its Key Issues and Research Progress[J]. Acta Geodaetica et Cartographica Sinica,1999,28(2):95-102.
[4]EGENHOFER M, FRANZOSA R. Point-set Topological Spatial Relations[J]. International Journal of Geographical Information Systems, 1991, 5 (2): 161-174.
[5]EGENHOFER M. A Model for Detailed Binary Topological Relationships[J]. Geomatic, 1993, 47(3):261-273.
[6]CHEN Jun, LI Cheng-ming, LI Zhi-lin, et al. A Voronoi-based 9-intersection Model for Spatial Relations[J]. International Journal of Geographical Information Science,2001, 15(3): 201-220.
[7]LI Zhi-lin, ZHAO Ren-liang, CHEN Jun. A Generic Algebra for Spatial Relations [J]. Progressing in Natural Science, 2002, 12(7): 528-536.
[8]ZHAO Ren-liang. A Voronoi-based Computing Method for Spatial Relations[D]. Changsha: School of Info-physics and Geomatics Engineering, Central South University, 2002.
[9]EGENHOFER M, CLEMENTINI E, P, FELICE di. Topological Relations between Regions with Holes[J]. International Journal of Geographical Information Systems, 1994, 8 (2): 129-144.
[10]Oracle Corporation. Oracle Spatial User′s Guide and Reference [EB/OL]. http://otn.oracle.com/documentation/spatial.html, 2003-12-10.

收稿日期:2004-06-24

基金项目:国家自然科学基金资助项目(40301042); 辽宁工程技术大学地理空间信息技术与应用实验室基金资助项目(2004009)

作者简介:周晓光(1969-),女,湖南岳阳人,副教授,从事GIS研究

论文联系人: 周晓光,女,副教授;电话:0731-8877060(H),13875972482(手机); E-mail: zxg@mail.csu.edu.cn