
DOI: 10.11817/j.issn.1672-7207.2021.03.033
高应力环境水平矿柱尺寸演变过程力学响应及稳定性
吴顺川,李天龙,程海勇,张小强,赵志强
(昆明理工大学 国土资源工程学院,云南 昆明,650093)
摘要:甘肃某矿高应力回采区域采用下向水平分层六角形进路式充填采矿法,双中段大盘区同时回采的模式。矿体水平应力大,最大主应力方向基本垂直于矿体走向,且接近水平。水平矿柱随着开挖而逐渐形成至变薄消失,同时上部充填体越来越厚,在整个生产过程中水平矿柱尺寸大,很难监控其内部应力分布情况。通过力学解剖水平矿柱形成过程,总结水平矿柱稳定性分析方法,探究基于充填体-围岩拱效应的水平矿柱稳定性。结合数值模拟算法和工程实例,分析水平矿柱中的主应力变化特征、塑性区分布特点以及位移变化规律。研究结果表明:在高应力环境,当水平矿柱厚度降至30 m左右时,应力集中现象逐渐显现;靠近上盘的进路更容易产生侧向挤压变形,并出现顶板冒落;最大主应力一般出现在水平矿柱底部,当水平矿柱厚度降至一定水平,出现明显应力转移,充填体起到承压作用,水平矿柱内的应力集中和位移沉降得到一定程度缓解。通过研究水平矿柱稳定性,有效分析双中段同时回采时的可靠性及矿柱回收的安全性,有效防控大面积失稳灾害。
关键词:双中段回采;稳定性;水平矿柱;充填体-围岩拱效应;数值模拟
中图分类号:TD322 文献标志码:A 开放科学(资源服务)标识码(OSID):
文章编号:1672-7207(2021)03-1027-13
Mechanical response and stability of horizontal pillar size evolution in high stress environment
WU Shunchuan, LI Tianlong, CHENG Haiyong, ZHANG Xiaoqiang, ZHAO Zhiqiang
(School of Faculty of Land Resource Engineering, Kunming University of Science and Technology, Kunming 650093, China)
Abstract: A mine in Gansu Province was located in high stress mining area. The downward horizontal slicing hexagonal drift stopping method and the double middle large panel mining mode were adopted. The horizontal stress of the ore body was large, and the direction of the maximum principal stress was basically perpendicular to the strike of the ore body and close to the horizontal. With the excavation, the horizontal pillars gradually formed to thin and disappeared, and the upper filling body became thicker and thicker. In the whole production process, the size of the horizontal pillars was large, and its internal stress distribution was difficult to monitor. When the double-level mining was used in the mine, the horizontal pillar had a process from thick to thin or even disappeared completely. In the process of the horizontal pillar thickness evolution, the mechanical response of pillar was also changing dynamically, which had a profound impact on mine production safety. Through the mechanical analysis of the formation process of the horizontal pillar, the stability analysis method of the horizontal pillar was summarized, and the stability of the horizontal pillar based on the filling-surrounding rock arch effect was explored. Combined with numerical simulation algorithm and engineering example analysis, the characteristics of the maximum principal stress, the distribution of plastic zone and the rule of displacement change in horizontal pillar were analyzed. The results show that in the high stress environment, when the thickness of the horizontal pillar decreases to about 30 m, the phenomenon of stress concentration gradually appears. The access road close to the hanging wall is more likely to produce lateral extrusion deformation and roof caving. The maximum principal stress generally occurs at the bottom of the horizontal pillar. When the thickness of the horizontal pillar decreases to a certain level, there is an obvious stress transfer, the filling body plays a role of pressure bearing, and the stress concentration and displacement settlement in the horizontal pillar are relieved to a certain extent. Through the study of the stability of horizontal pillars, the reliability of double middle section mining and the safety of pillar recovery are effectively analyzed, and the effective prevention and control of large-scale instability disaster is realized.
Key words: double middle mining; stability; horizontal pillar; filling-surrounding rock arch effect; numerical simulation
未来10~15 a,我国将有50%铁矿资源、33%有色金属资源以及53%煤炭资源开采进入1 km以下,千米级深部资源开采已成为常态[1]。与地下浅部工程相比,深地岩体赋存环境复杂,深地巷道围岩表现出特有的力学特征,采区地应力将达到45 MPa以上,围岩的大变形、强流变性以及动力响应的突变性等问题将引发重大安全隐患。在深部资源开采过程中多采用双中段同时回采模式,双中段回采过程中将形成由厚至薄动态变化的水平矿柱。水平矿柱在不断变薄的过程中需要承担异常复杂的高应力扰动和应力转移[2]。水平矿柱的稳定性成为制约矿山生产安全和保障生产进度的重要因素。
传统意义上,理论分析、经验公式、安全系数评价、物理相似模型以及数值模拟等手段是研究采场稳定性的主要方法。姚高辉等[3]通过扩展后的Hoek-Brown节理强度准则分析破碎围岩条件下的采场留存矿柱的岩体力学参数,确定矿柱安全存留尺寸;邹洋等[4]通过普氏拱理论建立矿柱合理宽度计算模型,并采用数值模拟方法进行验证,实现采空区危险性分级;徐晓鼎等[5]运用能量理论分析采空区塑性支撑系统,构建支撑系统尖点突变模型,得到支撑体系相关的失稳判别条件;张涛等[6]对比宽度折减法和Lunder经验公式得到的水平矿柱厚度,提出了矿柱的临界宽度;赵兴东[7]采用极限跨度法、经验公式法以及极限平衡分析方法,分析隔离矿柱尺寸,并采用FLAC验算深部开采隔离矿柱稳定性;陈顺满等[8]为研究深部回采过程中矿柱稳定性影响因素的敏感程度,运用BIENIAWSKI矿柱强度公式推导了方形矿柱安全系数计算公式;罗斌玉等[9]根据应力圆与Mohr-Coulomb强度包络线之间的关系,建立考虑矿体倾角及矿柱受正应力和剪应力共同作用下矿柱的安全系数解析式;宋卫东等[10]根据矿柱载荷、强度、失稳形式及影响因素,确定等推导出安全系数计算公式,研究主要影响因素与矿柱安全系数之间的函数关系;ZHOU等[11-12]利用Fisher判别、支持向量机和贝叶斯理论等,识别地下矿山矿柱稳定性,预测水平矿柱的安全系数;余伟健等[13-14]采用平均压应力、平均剪应力和屈服比3个指标评价水平矿柱稳定性;ESTERHUIZEN等[15]基于现场监测结果和FLAC3D数值模型,分析长壁回采顶板的稳定性,利用模型比较载荷路径和地面响应,证明数值模型在优化长壁布置方面的潜力;SHERIZADEH等[16]采用3DEC数值模拟,评价矿柱尺寸对顶板的稳定性影响,发现地质条件和开采因素是影响顶板稳定性的重要因素,其中层理面影响最大;李夕兵等[17]应用中厚板理论建立FLAC3D隔离矿柱模型,得出安全厚度为20 m;马卓宇等[18]应用FLAC3D数值模拟软件,建立矩形进路的矿柱稳定性分析模型,确定最优的矿柱厚度为24 m;刘杰等[19]分析某露天转地下矿山的稳定性,采用强度折减法和FLAC3D数值模拟方法,得出不留境界矿柱的地下回采过程中,覆盖层厚度要至少25 m;徐文斌等[20]分析某金属矿山阶段嗣后充填矿柱破坏机理,进行FLAC3D数值模拟,建立阶段嗣后矿柱失稳演化模型,得到矿柱破坏方式和采场失稳演化过程;周科平等[21]基于BP神经网络嵌入FLAC3D,对水平矿柱进行强度折减进行数值模拟;LIU等[22]通过极限分析法嵌入FLAC3D,分析水平矿柱稳定性。由于水平矿柱材料性质和应力特性复杂[23-24],通过单一理论和方法进行水平矿柱稳定性研究具有局限性[25]。
本文对水平矿柱形成过程进行力学解析,总结水平矿柱稳定性分析方法,探究基于充填体-围岩拱效应的水平矿柱稳定性,并结合数值模拟技术分析水平矿柱稳定性,以期实现深部高应力环境中双中段同时回采的安全性。
1 水平矿柱形成过程与力学解析
1.1 水平矿柱形成过程
采用下向水平分层充填采矿法[26-27]对矿山双中段同时开采时,由分段道掘进分层联络道至矿体,以层为单位进行矿体回采,上中段和下中段同时作业。每层回采完毕后进行充填,充填体达到一定强度时可作为下一分层的顶板,在这一高强顶板的保护作用下进行下一分层的采充作业。随着开采,上中段充填体越来越厚,矿体越来越薄,在上中段回采进路和下中段首层充填体之间便形成应力显著集中的水平矿柱。水平矿柱形成过程如图1所示。
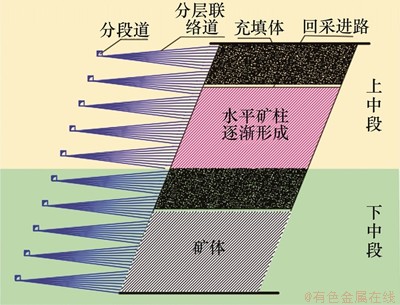
图1 水平矿柱形成过程
Fig. 1 Formation process of horizontal pillars
在深部高应力环境,水平矿柱内部应力转移和应力集中现象逐渐凸显[28]。当回采至某一分层时,水平矿柱内部应力集中现象大幅增加,甚至发生大范围应力释放,引起水平矿柱的严重破坏,改变整个生产中段的应力生态,对生产安全形成重大威胁,甚至引发不可恢复的生产中断。
1.2 水平矿柱力学解析
采用水平进路式充填采矿法时,每条进路分多次进行充填作业,充分保证采场接顶率,故在力学分析和模拟中均采用接顶假设。当水平矿柱发展到某一阶段,可认为水平矿柱整体符合平板梁力学模型,其简化力学模型如图2所示。
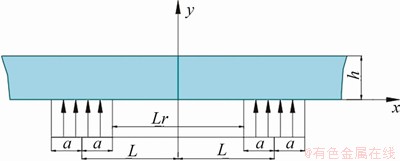
图2 双中段回采水平矿柱力学模型
Fig. 2 Force model of horizontal pillar in double-level mining
根据图2,将水平矿柱稳定性问题简化为理想弹性平面问题,应力状态如式(1)~(2)所示。
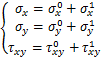 (1)
(1)
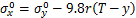 (2)
(2)
式中: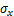 和
和 分别为x和y方向正应力;
分别为x和y方向正应力;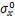 和
和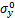 为x和y方向正应力初始值;
为x和y方向正应力初始值;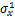 和
和 分别为x和y方向正应力增量;
分别为x和y方向正应力增量;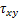 为剪切应力;
为剪切应力; 为剪切应力初始值;
为剪切应力初始值; 为剪切应力增量;
为剪切应力增量; 为矿石容量,kN/m3;T为矿柱厚度,m。
为矿石容量,kN/m3;T为矿柱厚度,m。

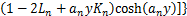 (3)
(3)

 (4)
(4)

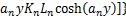 (5)
(5)
式中: ;
;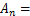
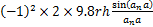 ;L为矿柱至矿房中心距离,m;a为1/2矿柱宽度,
;L为矿柱至矿房中心距离,m;a为1/2矿柱宽度,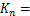
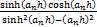 ;
;
 。
。
考虑设备行走等因素,可以得到全应力分析公式:
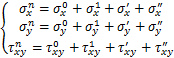 (6)
(6)
式中: 和
和 分别为设备自重载荷对矿柱的x和y方向应力;
分别为设备自重载荷对矿柱的x和y方向应力; 和
和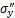 分别为设备行走动载荷对矿柱的x和y方向应力;
分别为设备行走动载荷对矿柱的x和y方向应力;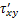 为设备自重载荷对矿柱的剪切应力;
为设备自重载荷对矿柱的剪切应力; 为设备行走载荷对矿柱的剪切应力。
为设备行走载荷对矿柱的剪切应力。
2 水平矿柱稳定性分析方法
2.1 水平矿柱破坏模式
水平矿柱是双中段同时回采至一定程度的产物,在下向水平分层开采过程中,水平矿柱的破坏失稳是渐进发生的。图3所示为水平矿柱内应力分布形式。由图3(a)可见:在水平矿柱厚度足够大时,矿柱内部载荷均匀分布,矿柱破坏形式以局部破坏为主。由图3(b)可见:当水平矿柱厚度降低至某一水平时,矿柱内应力场以“拱形”分布为主,矿柱破坏形式演变为以大型突发性破坏为主[29]。
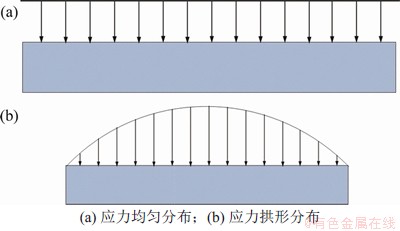
图3 水平矿柱内应力分布形式
Fig. 3 Distribution form of internal stress in horizontal pillar
水平矿柱的破坏模式主要受自身性质以及外部环境影响。图4所示为几种典型水平矿柱破坏模式。
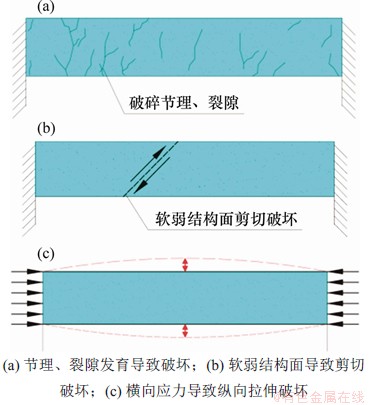
图4 几种典型水平矿柱破坏模式
Fig. 4 Several typical failure modes of horizontal pillars
由图4(a)可见:如果水平矿柱在采动等动力学影响下发育节理裂隙,在高应力环境,水平矿柱易产生岩体垮落和质量劣化等破坏。由图4(b)可见:如果水平应力增强至某一程度,矿柱内的节理裂隙等软弱结构面发育贯穿性裂隙,产生剪切破坏。由图4(c)可见:如果水平应力场持续增强,在高水平应力作用下,产生纵向拉伸破坏。
2.2 经典稳定性分析方法
水平矿柱稳定性主要受矿柱高跨比、矿柱尺寸和岩体稳定性等参数综合影响。矿柱稳定性分析方法主要有固定梁理论、厚跨比法、荷载传递线交汇法、结构力学简华梁法、普氏拱理论估算法、K.B.卢佩涅伊特理论估算法、极限平衡发以及数值模拟分析方法。下面对几种典型的理论算法进行分析。
1) 固定梁理论[30]
将水平矿柱视为两端固定的平板梁,结合全应力分析公式,考虑上覆均布载荷及矿柱自重作用,以抗弯失稳为准则,获得水平矿柱厚度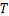 计算公式:
计算公式:
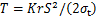 (7)
(7)
式中: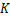 为安全系数,取
为安全系数,取 ;
; 为水平矿柱的跨度,m;
为水平矿柱的跨度,m;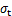 为岩石抗拉强度,MPa。
为岩石抗拉强度,MPa。
由此可见,在保证稳定性条件下,矿柱厚度随空区跨度呈指数增长。水平矿柱厚度过大,将形成较大资源损失率;水平矿柱厚度过小,将严重影响采场稳定性,形成安全威胁。
2) K.B.鲁别涅伊特公式[31]
K.B.鲁别涅伊特主要考虑空区跨度及顶柱岩体特性(强度及构造破坏特性)对安全顶柱厚度的影响,同时也考虑水平矿柱上部充填体的作用,提出安全厚度计算公式如下:
 (8)
(8)
式中:B为空区跨度,m;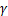 为充填体密度,kg/m3;
为充填体密度,kg/m3; ,为在弯曲条件下岩石强度极限,考虑到强度安全系数
,为在弯曲条件下岩石强度极限,考虑到强度安全系数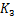 和结构削弱系数
和结构削弱系数 条件下顶板强度极限,MPa;
条件下顶板强度极限,MPa; 为岩石单轴抗压强度,MPa;
为岩石单轴抗压强度,MPa;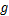 为水平矿柱上方的充填体对水平矿柱的压力,MPa。
为水平矿柱上方的充填体对水平矿柱的压力,MPa。
3) 极限平衡法[[32]
水平矿柱上覆岩层包括上盘围岩、充填体以及水压作用,可以利用微分条块办法划分计算重力和剪应力,微分条块数量越多计算结果越精确。在考虑每一微分条块不同物理力学指标的同时,就可以应用极限平衡法估算水平矿柱极限高度,开挖后,采空区上覆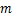 条岩层(对于
条岩层(对于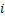 条厚度
条厚度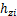 )重力与侧边剪力比值
)重力与侧边剪力比值 为:
为:
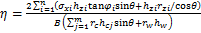 (9)
(9)
式中: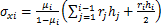 ,
,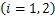 为水平应力,MPa;
为水平应力,MPa;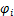 ,
,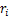 和
和 分别为岩层的内摩擦角、容重和泊松比。
分别为岩层的内摩擦角、容重和泊松比。
4) 数值分析
高地应力环境下水平矿柱形成过程复杂,采用理论分析和室内试验等方法难以真实还原其演变过程。数值分析方法可分析大尺度岩体开挖工程,模拟开挖时岩体内应力和应变的分布情况、岩体破坏形式和破坏程度。FLAC3D分析步骤一般可分为建立数值模型、材料参数赋值和边界条件约束等,计算完成后,通过云图分析和监测点的过程监控,分析工程体所处应力和位移情况。
经典理论分析法基于外加均布荷载,经过了合理简化。K.B.鲁别涅伊特理论考虑生产实际因素较多,计算过程复杂且效率低。固定梁理论和极限平衡法考虑因素相对较少,计算结果较保守,易造成资源浪费。数值模拟能够在矿体尺度精细化预知水平矿柱随开采进度的稳定性,其结论具有重要工程意义。
3 基于充填体-围岩拱效应的水平矿柱稳定性
3.1 基本假设
根据弹性力学理论,假设:
1) 矿体及充填体是均匀、各向同性的材料[33-34];
2) 矿体及充填体2种介质是完全弹性的;
3) 充填体及水平矿柱受力后,各质点位移远小于原物体尺寸;
4) 矿柱受到充填体的垂直应力 视为均布荷载。
视为均布荷载。
3.2 充填体-围岩耦合应力分析模型
水平矿柱纵向受到顶柱和充填体重力作用和围岩侧向挤压作用,垂直荷载是矿柱破坏的主要原因。拱效应是在充填体-围岩耦合状态下的特定结构,导致垂直应力小于自身重力的现象。吴爱祥等[35]发现窄长型充填体的拱架效应,可降低围岩垂直应力;姜立春等[36]建立充填体拱效应水平矿柱分析模型,计算出水平矿柱的预留安全厚度。本文在充填体拱效应的基础上,充分考虑围岩影响,建立充填体-围岩拱效应模型。充填体-围岩拱效应影响下垂直应力的变化如图5所示。深部环境下充填体的垂直应力分布可采用Thomas公式进行分析:
 (10)
(10)
式中: 为作用在充填体的垂直应力,MPa;
为作用在充填体的垂直应力,MPa;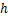 为充填体的高度,m;
为充填体的高度,m; 为充填体宽度,m。
为充填体宽度,m。
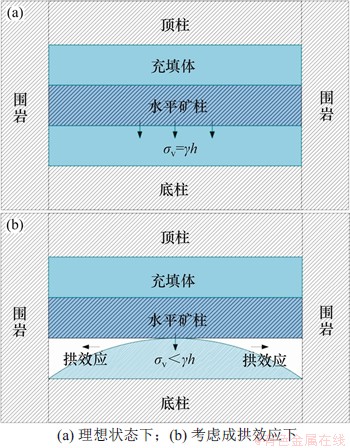
图5 充填体-围岩拱效应下垂直应力分布
Fig. 5 Vertical stress distribution under effect of backfill surrounding rock arch
3.3 水平矿柱稳定性
基于充填体-围岩拱效应理论,在双中段同时回采过程中,水平矿柱不断变薄,且由于其高度一般都远小于其跨度,故可将水平矿柱视为桥拱。
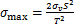 (11)
(11)
根据第一强度准则,当最大拉应力 超过拉应力允许值
超过拉应力允许值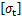 时,岩体将发生破坏。
时,岩体将发生破坏。 应满足:
应满足:
 (12)
(12)
根据Hoek-Brown准则:
 (13)
(13)
式中: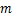 和
和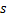 为与岩性及结构面情况有关的常数,
为与岩性及结构面情况有关的常数,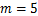 ,
,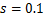 。因此,水平矿柱的安全厚度表达式可表述为:
。因此,水平矿柱的安全厚度表达式可表述为:
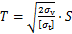 (14)
(14)
考虑水平矿柱下部矿体被采出后,当水平矿柱下部充填体未被压缩到承压状态时,水平矿柱只依靠自身强度维持稳定。基于充填体-围岩拱效应的水平矿柱稳定性分析模型,考虑深部高应力环境下的原岩应力和充填体特性,该模型分析速度快,同时具有较广的识别范围。
4 工程分析
4.1 工程概况
甘肃某镍矿处于高应力回采区域,最大主应力为30~50 MPa,方向接近水平。该矿区设计生产能力245万t/a,采用双中段同时回采模式进行资源回收。矿体平均真厚为100 m左右,平均倾角为70°,上盘围岩为混合岩,下盘围岩为大理岩,矿体顶部围岩为二辉橄榄岩,矿山各部分的岩体力学参数如表1所示。
表1 岩体力学参数
Table 1 Mechanical parameters of rock mass

矿山采用应力解除法和改进型空心包体应变计测量技术,测量矿区3个中段10个监测点的地应力,分析该矿区深部地应力的分布规律,并利用线性回归的方法得出最大水平主应力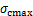 随深度变化的回归方程:
随深度变化的回归方程:
 (15)
(15)
充填体-围岩拱效应影响下水平矿柱实际垂直应力的可行域为:
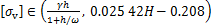 (16)
(16)
式中: 为水平矿柱实际垂直应力;H为矿体深度。
为水平矿柱实际垂直应力;H为矿体深度。
根据该矿区的岩体力学参数和地应力状态,水平矿柱可能存在拉破坏或剪切破坏,故针对水平矿柱形成特点,结合地应力分布规律和充填体强度分析,基于充填体-围岩拱效应模型建立水平矿柱最大主应力的分布函数,得出最大主应力的可行域,如图6所示。
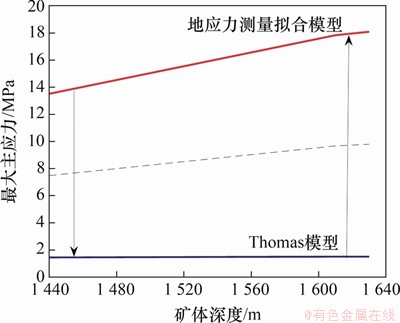
图6 最大主应力随矿体深度变化特征
Fig. 6 Variation characteristics of maximum principal stress with ore body depth
采用充填体-围岩耦合分析模型研究水平矿柱稳定性。若采用分层一次性揭露,采场走向长度为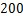 m,沿矿体宽度为
m,沿矿体宽度为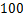 m,将上述参数代入式(14),得到式(17):
m,将上述参数代入式(14),得到式(17):
 (17)
(17)
由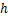 与
与 的关系式绘制曲线,如图7所示。由图7可见:随着最大主应力增加,水平矿柱预留厚度非线性增长,当最大主应力为20~80 MPa时,水平矿柱应预留厚度达到28.3~56.6 m,这将形成巨大的资源损失率。
的关系式绘制曲线,如图7所示。由图7可见:随着最大主应力增加,水平矿柱预留厚度非线性增长,当最大主应力为20~80 MPa时,水平矿柱应预留厚度达到28.3~56.6 m,这将形成巨大的资源损失率。
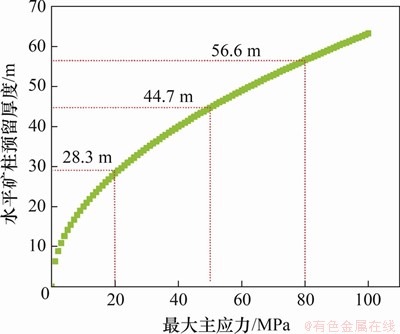
图7 矿柱厚度随最大主应力变化特征
Fig. 7 Variation characteristics of thickness of reserved pillar with maximum principal stress
为克服上述问题,降低高地应力环境对采矿活动带来的安全风险,矿山采用进路式充填采矿方案,最大限度减少暴露面积。同时为有效缓解高应力对进路的破坏程度,采用具有生态学稳定结构的六角形进路形式,六角形底宽为4 m,高为5 m,腰宽为6 m。在六角形镶嵌结构形态下,水平矿柱的稳定性可通过数值分析手段进行精细化描述。
4.2 双中段同时开采水平矿柱数值模型
根据所研究的问题和矿山开采现状,建立数值模型,模型X方向即垂直于矿体走向,长为830 m,模型Y方向即沿矿体走向,为500 m,模型Z方向即竖直方向高度为720 m。采矿方式为双中段同时回采,六角形全断面一次性开挖。模型总网格数55万。岩体力学参数根据矿山前期研究成果获取,应力状态根据充填体-拱效应耦合应力分析结果赋值。同时在不同分层布设监测点,监测开挖时各监测点的应力及位移状态。在1 540 m关键分段的3个典型分层布设30个水平监测点,沿矿体纵剖面布设16个竖直监测点,监测点分布位置如图8所示。
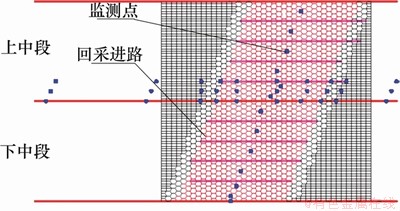
图8 监测点分布位置
Fig. 8 Distribution of monitoring points
4.3 主应力与X向位移随开挖进程响应特征
模拟试验共进行14步开挖充填过程,水平矿柱最大主应力演变如图9所示。在开挖至第6步之前,水平矿柱内部应力均匀分布在16 MPa左右;后期开挖中应力集中现象显著,开挖至第10步时,水平矿柱内最大主应力达到15.0~22.5 MPa,高于同水平上下盘处应力12.5 MPa左右,水平矿柱的应力已达到最大值;第12步开挖后,最大主应力降低至7.5~15.0 MPa,表明水平矿柱回采至一定程度后,应力集中程度有减弱趋势,标志着最危险时期已经过去;第14步开挖后,上中段充填体内最大主应力为1.1~2.5 MPa,下中段充填体内最大主应力为2.5~7.5 MPa,水平矿柱实现全部回采。
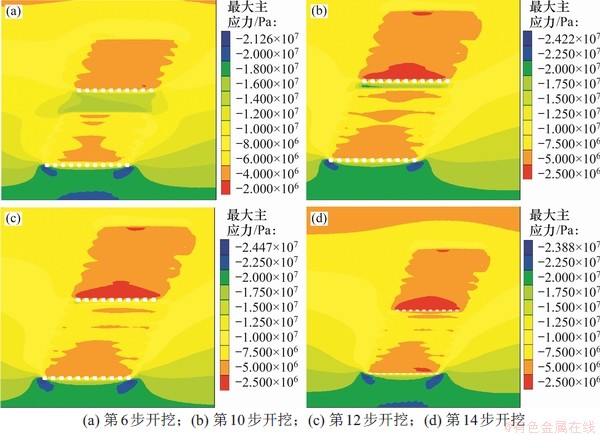
图9 水平矿柱最大主应力随开挖进程响应
Fig. 9 Response of maximum principal stress with excavation progress of horizontal pillar
水平矿柱各阶段的最小主应力随开挖进程变化如图10所示。由图10可见:第6步开挖后,水平矿柱内最小主应力为2~3 MPa,越靠近上下盘的位置最小应力越大,最大达5~6 MPa。第10步开挖后,水平矿柱可能的破坏形式为压破坏或剪切破坏。第12步开挖后,水平矿柱最小主应力为0.1~2.0 MPa,拉破坏可能性下降。
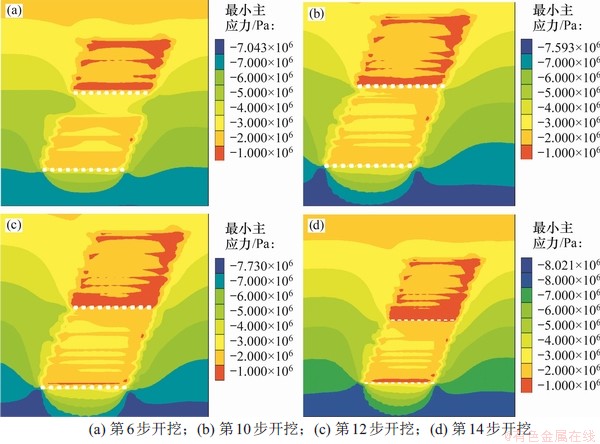
图10 水平矿柱最小主应力随开挖进程响应
Fig. 10 Response of the minimum principal stress with excavation process of horizontal pillar
统计分析发现,开挖过程中X方向水平位移现象显著,岩体移动范围明显,并表现出典型的收缩性移动,即上盘岩体向下盘方向移动,下盘岩体向上盘方向移动。开挖进程中X方向位移响应如图11所示。上盘岩体从开挖至结束时移动量最大为47 mm,下盘岩体最大岩移动量为40 mm。大规模的岩体移动将导致靠近上下盘进路的严重变形。在上下盘进路开挖时应加强支护和卸压措施。
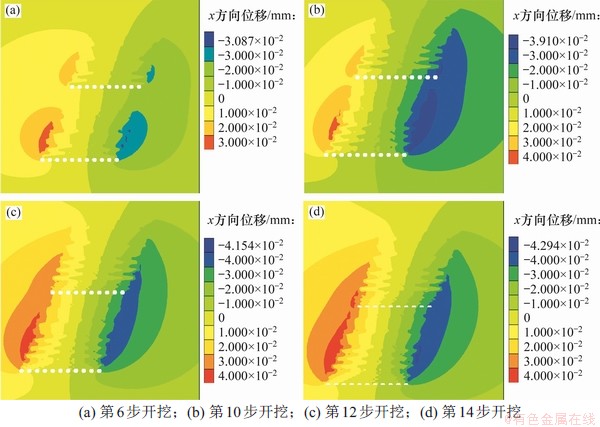
图11 开挖进程中X方向位移响应
Fig. 11 X-direction displacement response with excavation process
4.4 塑性区随开挖进程分布规律
分析开挖进程中的塑性区分布如图12所示。由图12可见:
1) 第6步开挖后,水平矿柱曾出现剪切屈服和拉伸屈服,在上下盘位置及开挖进路底板处曾出现剪切屈服。
2) 第10步开挖后,水平矿柱全部处于塑性区,曾出现剪切屈服。以往开挖进路中的充填体在本步开挖中曾出现剪切屈服和拉伸屈服,在充填体和围岩交界处曾出现剪切屈服。
3) 第12步开挖后,水平矿柱内部经历过剪切屈服,但在水平矿柱上下盘部分位置正在发生剪切屈服,岩体的整体稳定性较差,开挖时岩体有可能产生垮落现象。
4) 第14步开挖后,进路附近未有正在发生的剪切屈服,本层进路回采未出现大规模的力学扰动,稳定性良好。
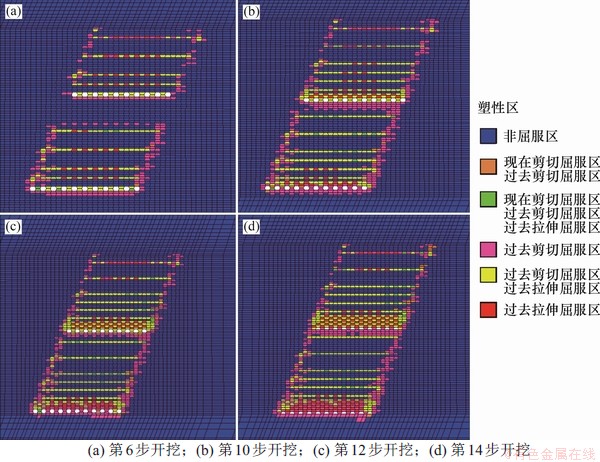
图12 塑性区随开挖进程分布
Fig. 12 Distribution of plastic zone with excavation process
4.5 最大主应力响应规律
1) 不同深度监测点应力状态
由图13可见:在距离地表190~220 m处,应力集中现象较明显。并随着深度增加,最大主应力逐渐增大。水平矿柱的最低位置即220 m处,在开挖第10步时应力集中最大值达到16.3 MPa,在下中段的最低水平也逐渐出现应力集中现象,最大应力为18.25 MPa。由此可见,应力集中现象主要在水平矿柱内,在开挖第10步时,水平矿柱内的应力达到最大,在开挖至11步以后,最大主应力又逐渐减小,并随着充填最终趋于稳定。
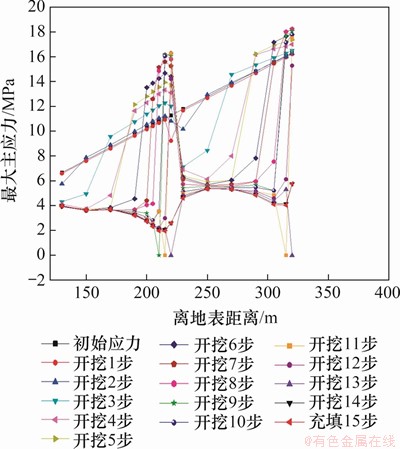
图13 不同深度监测点最大主应力变化曲线
Fig. 13 Change curve of maximum principal stress of each monitoring point at different depths
2) 不同水平监测点应力状态
在1 540 m和1 560 m水平各布置10个监测点,分布如图14所示。由图14可见:不同水平上下盘围岩及矿体内的初始状态最大主应力分布几乎在同一水平。但随着开挖,上下盘围岩及矿体内最大主应力分布表现出巨大差异。在上盘,越靠近矿体最大主应力波动范围越大,且最大主应力表现出往小值波动,开挖过程中最大主应力均小于初始状态的最大主应力。在下盘同样表现出同样变化规律。在矿体内部则表现出越靠近上盘,水平矿柱内最大主应力集中程度越高,下盘次之,矿体中间部位最大主应力集中程度最弱。1 560 m水平靠近矿体上盘最大主应力最大值为13.53 MPa,高于初始应力3.01 MPa。在1 540 m水平靠近矿体上盘出现的最大值为18.32 MPa,高于初始应力7.03 MPa。
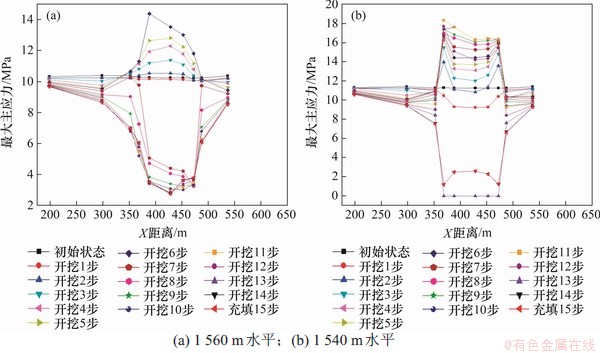
图14 水平矿柱内同水平监测点最大主应力随X距离变化
Fig. 14 Maximum principal stress of same horizontal monitoring point in horizontal pillar changes with X distance
综合上述分析可以判断,水平矿柱厚度在剩余10~20 m范围时,最大主应力集中现象较显著,在靠近上下盘进路易出现压缩变形破坏。在水平矿柱厚度小于10 m以下时,发生大规模应力转移现象,水平矿柱内应力状态基本稳定。
5 结论
1) 随着双中段同时开挖的不断推进,当水平矿柱厚度降低至10~30 m时,水平矿柱内应力集中现状逐渐显著,应力集中程度最大达22.5 MPa。在此阶段,进路可能存在垮塌、底板底鼓和顶板冒落等现象。尤其靠近上盘进路最容易产生巷道变形及顶板冒落,上盘部分进路存在整体垮塌失稳的可能性,下中段开挖进路底鼓现象较严重。
2) 危险阶段发生在水平矿柱厚度剩余10~20 m时,靠近上盘的进路经历过剪切屈服,岩体整体稳固性较差,最容易产生巷道侧向挤压变形和顶板冒落。
3) 当水平矿柱厚度降至10 m以下时,发生大规模应力转移现象,充填体吸收部分应力,水平矿柱内应力较低,并且状态稳定。在充填体的保护作用下,水平矿柱可安全回收。
4) 水平矿柱最危险状态并非随矿柱尺寸线性增强,而是发生在矿柱厚度为10~20 m范围附近,此时应加强监测,并根据监测状态设置永久矿柱。
参考文献:
[1] 吴爱祥, 李红, 程海勇, 等. 全尾砂膏体流变学研究现状与展望(上): 概念、特性与模型[J]. 工程科学学报, 2020, 42(7): 803-813.
WU Aixiang, LI Hong, CHENG Haiyong, et al. Status and prospects of researches on rheology of paste backfill using unclassifiedtailings(Part 1): concepts, characteristics and models[J]. Chinese Journal of Engineering, 2020, 42(7): 803-813.
[2] 陈庆发, 杨承业, 尹庭昌, 等. 金属矿山矿块单元结构体组合关系研究[J]. 岩土力学, 2020, 41(S1): 74-82.
CHEN Qingfa, YANG Chengye, YIN Tingchang, et al. Combination relationship of ore block structures in metal mines[J]. Rock and Soil Mechanics, 2020, 41(S1): 74-82.
[3] 姚高辉, 吴爱祥, 王贻明, 等. 破碎围岩条件下采场留存矿柱稳定性分析[J]. 北京科技大学学报, 2011, 33(4): 400-405.
YAO Gaohui, WU Aixiang, WANG Yiming, et al. Stability analysis of stope retention Pillars in broken rock conditions[J]. Journal of University of Science and Technology Beijing, 2011, 33(4): 400-405.
[4] 邹洋, 李夕兵, 赵国彦, 等. 石膏矿采空区上覆岩层冒落规律与危险性评价[J]. 中国安全科学学报, 2011, 21(2): 101-108.
ZOU Yang, LI Xibing, ZHAO Guoyan, et al. Study on the caving laws of overlying strata in gypsum mine goaf and its risk assessment[J]. China Safety Science Journal, 2011, 21(2): 101-108.
[5] 徐晓鼎, 周跃进, 庞顺. 石膏矿老采空区塑性支撑系统的突变失稳分析[J]. 岩石力学与工程学报, 2018, 37(11): 2548-2555.
XU Xiaoding, ZHOU Yuejin, PANG Shun. Analysis of catastrophic instability of plastic supporting system in old goaf of gypsum mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(11): 2548-2555.
[6] 张涛, 张帅, 张百胜. 矿柱安全留设尺寸的宽度折减法与应用[J]. 岩土力学, 2014, 35(7): 2041-2046.
ZHANG Tao, ZHANG Shuai, ZHANG Baisheng. Width reduction method and its application to determining safety size of pillar[J]. Rock and Soil Mechanics, 2014, 35(7): 2041-2046.
[7] 赵兴东. 谦比希矿深部开采隔离矿柱稳定性分析[J]. 岩石力学与工程学报, 2010, 29(S1): 2616-2622.
ZHAO Xingdong. Stability analysis of insulating pillar of excavation of chambishi copper mine in depth[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 2616-2622.
[8] 陈顺满, 吴爱祥, 王贻明, 等. 深部回采矿柱稳定性影响因素分析及其应用[J]. 中南大学学报(自然科学版), 2018, 49(8): 2050-2057.
CHEN Shunman, WU Aixiang, WANG Yiming, et al. Analysis of influencing factors of pillar stability and its application in deep mining[J]. Journal of Central South University(Science and Technology), 2018, 49(8): 2050-2057.
[9] 罗斌玉, 叶义成, 李玉飞, 等. Mohr-Coulomb准则下倾斜矿柱稳定性的安全系数法[J]. 煤炭学报, 2018, 43(9): 2408-2415.
LUO Binyu, YE Yicheng, LI Yufei, et al. Safety factor method for stability of inclined Pillars under Mohr-Coulomb criterion[J]. Journal of China Coal Society, 2018, 43(9): 2408-2415.
[10] 宋卫东, 曹帅, 付建新, 等. 矿柱稳定性影响因素敏感性分析及其应用研究[J]. 岩土力学, 2014, 35(S1): 271-277.
SONG Weidong, CAO Shuai, FU Jianxin, et al. Sensitivity analysis of impact factors of pillar stability and its application[J]. Rock and Soil Mechanics, 2014, 35(S1): 271-277.
[11] ZHOU Jian, LI Xibing, SHI Xiuzhi, et al. Predicting pillar stability for underground mine using Fisher discriminant analysis and SVM methods[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2734-2743.
[12] HU Yuxi, LI Xibing. Bayes discriminant analysis method to identify risky of complicated goaf in mines and its application[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 425-431.
[13] 余伟健, 高谦. 充填采矿优化设计中的综合稳定性评价指标[J]. 中南大学学报(自然科学版), 2011, 42(8): 2475-2484.
YU Weijian, GAO Qian. Stability evaluation indexes in optimization design of filling mining[J]. Journal of Central South University(Science and Technology), 2011, 42(8): 2475-2484.
[14] 刘增辉, 高谦. 两中段开采的水平矿柱失稳影响因素分析与方案优化-以金川二矿区为例[J]. 中国安全科学学报, 2013, 23(11): 79-84.
LIU Zenghui, GAO Qian. Analysis of factors influencing horizontal pillar instability and optimization of two-level mining plans-taking Jinchuan no.2 mine as an example[J]. China Safety Science Journal, 2013, 23(11): 79-84.
[15] ESTERHUIZEN G S, GEARHART D F, KLEMETTI T, et al. Analysis of gateroad stability at two longwall mines based on field monitoring results and numerical model analysis[J]. International Journal of Mining Science and Technology, 2019, 29(1): 35-43.
[16] SHERIZADEH T, KULATILAKE P H S W. Assessment of roof stability in a room and pillar coal mine in the US using three-dimensional distinct element method[J]. Tunnelling and Underground Space Technology, 2016, 59: 24-37.
[17] 李夕兵, 彭定潇, 冯帆, 等. 基于中厚板理论的深部崩落转充填隔离矿柱稳定性分析[J]. 中国矿业大学学报, 2019, 48(3): 484-494.
LI Xibing, PENG Dingxiao, FENG Fan, et al. Stability analysis of horizontal insulating pillar in deep mining from caving to filling method on the basis of refined plate theory[J]. Journal of China University of Mining & Technology, 2019, 48(3): 484-494.
[18] 马卓宇, 乔登攀, 唐进. 下向水平分层矩形进路膏体充填矿柱稳定性数值模拟研究[J]. 云南冶金, 2019, 48(4): 7-12.
MA Zhuoyu, QIAO Dengpan, TANG Jin. The numerical modeling study on stability of paste filling pillar at downward horizontal layered rectangular route[J]. Yunnan Metallurgy, 2019, 48(4): 7-12.
[19] 刘杰, 赵兴东, 路增祥. 露天转地下开采方案优化及边坡稳定性分析[J]. 东北大学学报(自然科学版), 2013, 34(9): 1327-1329.
LIU Jie, ZHAO Xingdong, LU Zengxiang. Mining scheme optimization and slope stability analysis for transition from open-pit to underground mining[J]. Journal of Northeastern University(Natural Science), 2013, 34(9): 1327-1329.
[20] 徐文彬, 宋卫东, 谭玉叶,等. 金属矿山阶段嗣后充填采场空区破坏机理[J]. 煤炭学报, 2012, 37(S1): 53-58.
XU Wenbin, SONG Weidong, TAN Yuye, et al. Failure mechanism of stope and exploited areas with stage backfill method in metal mine[J]. Journal of China Coal Society, 2012, 37(S1): 53-58.
[21] 周科平, 王星星, 高峰. 基于强度折减与ANN-GA模型的采场结构参数优化[J]. 中南大学学报(自然科学版), 2013, 44(7): 2848-2854.
ZHOU Keping, WANG Xingxing, GAO Feng. Stope structural parameters optimization based on strength reduction and ANN-GA model[J]. Journal of Central South University(Science and Technology), 2013, 44(7): 2848-2854.
[22] LIU Zhixiang, LUO Tian, LI Xiang, et al. Construction of reasonable pillar group for undersea mining in metal mine[J]. Transactions of Nonferrous Metals Society of China, 2018, 28(4): 757-765.
[23] 任红岗, 汪旭光, 谭卓英, 等. 采空区群蠕变突变三维力学模型构建及稳定性精确预测[J]. 中南大学学报(自然科学版), 2019, 50(12): 3114-3126.
REN Honggang, WANG Xuguang, TAN Zhuoying, et al. Construction of three-dimensional mechanical model for creep and catastrophe of goaf group and accurate prediction of its stability[J]. Journal of Central South University(Science and Technology), 2019, 50(12): 3114-3126.
[24] ZHOU Zilong, WANG Haiquan, CAI Xin, et al. Bearing characteristics and fatigue damage mechanism of multi-pillar system subjected to different cyclic loads[J]. Journal of Central South University, 2020, 27(2): 542-553.
[25] 于清军, 李元辉, 刘照朋, 等. 落矿冲击作用下矿柱结构参数优化与稳定性分析[J]. 中南大学学报(自然科学版), 2019, 50(5): 1181-1191.
YU Qingjun, LI Yuanhui, LIU zhaopeng, et al. Stability analysis and structural parameter optimization of pillar under impact of rockfall[J]. Journal of Central South University(Science and Technology), 2019, 50(5): 1181-1191.
[26] 吴爱祥, 杨莹, 程海勇, 等. 中国膏体技术发展现状与趋势[J]. 工程科学学报, 2018, 40(5): 517-525.
WU Aixiang, YANG Ying, CHENG Haiyong, et al. Status and prospects of paste technology in China[J]. Chinese Journal of Engineering, 2018, 40(5): 517-525.
[27] CHENG Haiyong, WU Shunchuan, LI Hong, et al. Influence of time and temperature on rheology and flow performance of cemented paste backfill[J]. Construction and Building Materials, 2020, 231: 117117.
[28] 赵国彦, 刘建, 周健. 基于不同判别准则的硬岩矿柱状态识别模型[J]. 中南大学学报(自然科学版), 2018, 49(11): 2813-2820.
ZHAO Guoyan, LIU Jian, ZHOU Jian. Recognition model of hard rock Pillars state based on different discriminant criterions[J]. Journal of Central South University(Science and Technology), 2018, 49(11): 2813-2820.
[29] 程海勇, 吴爱祥, 韩斌, 等. 露天-地下联合开采保安矿柱稳定性[J]. 中南大学学报(自然科学版), 2016, 47(9): 3 183-3192.
CHENG Haiyong, WU Aixiang, HAN Bin, et al. Stability of safety Pillars in opencast-underground combined mining[J]. Journal of Central South University(Science and Technology), 2016, 47(9): 3183-3192.
[30] 潘岳, 张勇, 吴敏应, 等. 非对称开采矿柱失稳的突变理论分析[J]. 岩石力学与工程学报, 2006, 25(S2): 3694-3702.
PAN Yue, ZHANG Yong, WU Minying, et al. Analysis of catastrophe theory for pillar destabilization in dissymmetric mining[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 3694-3702.
[31] 陆广, 罗周全, 刘晓明, 等. 露天转地下开采隔层厚度安全分析[J]. 采矿与安全工程学报, 2011, 28(1): 132-137.
LU Guang, LUO Zhouquan, LIU Xiaoming, et al. Safety analysis of interlayer thickness from open pit to underground mining[J]. Journal of Mining & Safety Engineering, 2011, 28(1): 132-137.
[32] FAN Xiaoming, REN Fengyu, XIAO Dong, et al. Opencast to underground iron ore mining method[J]. Journal of Central South University, 2018, 25(7): 1813-1824.
[33] CHENG Haiyong, WU Shunchuan, ZHANG Xiaoqiang, et al. A novel prediction model of strength of paste backfill prepared from waste-unclassified tailings[J]. Advances in Materials Science and Engineering, 2019(5): 1-10.
[34] CHENG Haiyong, WU Shunchuan, ZHANG Xiaoqiang, et al. Effect of particle gradation characteristics on yield stress of cemented paste backfill[J]. International Journal of Minerals, Metallurgy and Materials, 2020, 27(1): 10-17.
[35] 吴爱祥, 沈慧明, 姜立春, 等. 窄长型充填体的拱架效应及其对目标强度的影响[J]. 中国有色金属学报, 2016, 26(3): 648-654.
WU Aixiang, SHEN Huiming, JIANG Lichun, et al. Arching effect of long-narrow cemented paste backfill body and its effect on target strength[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(3): 648-654.
[36] 姜立春, 陈鹏. 基于充填体拱效应的水平矿柱安全厚度研究[J]. 金属矿山, 2018(6): 46-50.
JIANG Lichun, CHEN Peng. Study on safety thickness of horizontal pillar based on arch effect of backfilling[J]. Metal Mine, 2018(6): 46-50.
(编辑 秦明阳)
收稿日期: 2020 -04 -17; 修回日期: 2020 -07 -03
基金项目(Foundation item):中国博士后科学基金资助项目(2020T130272,2019M663576);国家自然科学基金资助项目(51934003,51774020);云南省高校科技创新团队(Projects(2020T130272, 2019M663576) supported by China Postdoctoral Science Foundation; Projects(51934003, 51774020) supported by the National Natural Science Foundation of China, Project supported by Program for Innovative Research Team (Science and Technology) in University of Yunnan Province)
通信作者:程海勇,博士后,副教授,从事膏体充填采矿与岩石力学研究;E-mail:haiker2007@163.com
引用格式: 吴顺川, 李天龙, 程海勇, 等. 高应力环境水平矿柱尺寸演变过程力学响应及稳定性[J]. 中南大学学报(自然科学版), 2021, 52(3): 1027-1039.
Citation: WU Shunchuan, LI Tianlong, CHENG Haiyong, et al. Mechanical response and stability of horizontal pillar size evolution in high stress environment[J]. Journal of Central South University(Science and Technology), 2021, 52(3): 1027-1039.