文章编号:1004-0609(2013)08-2309-07
基于扰动预测的氧化铝晶种分解过程建模与温度预测控制
刘 征1,彭小奇1, 2,汪明宏3,陈 君1
(1. 中南大学 信息科学与工程学院,长沙 410083;
2. 湖南第一师范学院 信息科学与工程系,长沙 410205;
3. 内蒙古鑫旺再生资源有限公司,鄂尔多斯 014300)
摘 要:分解温度是氧化铝晶种分解工序中的关键工艺参数。为精确控制分解温度,运用机理分析与参数辨识相结合的方法建立带板式换热器种分槽系统的非线性动态模型,并利用实际生产过程数据验证模型的正确性。提出一种基于不可测干扰预测的非线性模型预测控制(DP-NMPC)方法,利用时间序列分析方法建立系统中不可测扰动的自适应预测模型,并以此模型对分解温度预测模型进行校正。基于实际生产过程数据的仿真研究表明,相比常规NMPC,该方法提高了预测模型的精度,使控制系统能快速跟踪系统设定值,更好地抑制超调,因而其抗干扰能力更强,能对晶种分解温度进行有效控制。由于该方法适用于具有不可测非白噪声强干扰过程的模型预测控制,具有显著的实用价值。
关键词:氧化铝;晶种分解;扰动预测;非线性预测控制
中图分类号:TP273;TF355 文献标志码:A
Modeling and model predictive control of decomposition temperature in alumina precipitation based on disturbance prediction
LIU Zheng1, PENG Xiao-qi1, 2, WANG Ming-hong3, CHEN Jun1
(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;
2. Department of Information Science and Engineering, Hunan First Normal University, Changsha 410205, China;
3. Inner Mongolia Xinwang Renewable Resources Co., Ltd., Erdos 014300, China)
Abstract: The decomposition temperature is the key technological parameter in alumina seed precipitation process. In order to control the decomposition temperature precisely, a nonlinear dynamic model of the precipitator equipped with a plate heat exchanger in alumina tri-hydrate precipitation was built by mechanism analysis and parameter estimation, and the accuracy of the model was proved by the simulation with actual process data. A nonlinear model predictive control (DP-NMPC) method based on the unmeasured disturbances prediction was proposed, which applies the analysis of time series to build an adaptive predictive model of unmeasured disturbances in the precipitator system, and then revises the decomposition temperature predictive model. Comparing with the common NMPC, the proposed method is more effective in controlling decomposition temperature, which improves the accuracy of the predictive model, performs a quick following of set point changes, and has a better reduction of overshoot and a stronger rejection of disturbances. That method can be applied to the process with strong unmeasured nonwhite disturbances, and has remarkable practical value.
Key words: alumina; seed precipitation; disturbances prediction; nonlinear model predictive control
我国氧化铝产量和消费量占全世界的35%~40%,研究提高氧化铝产量和质量并降低成本和能耗的技术是我国铝工业可持续发展的重要途径之一[1]。晶种分解是拜尔法生产氧化铝工艺中耗时最长的关键工序,其分解率和分解质量直接影响氧化铝的产量和质量。许多研究实践[2-4]表明,实际生产过程中便于调节的分解温度是影响分解率和分解质量的关键工艺参数,应根据天气状况及时调整降温设备的操作参数,保证分解温度波动不超过0.5 ℃[5]。但目前的实际生产中,各种分槽的分解温度由操作人员根据生产经验调节中间降温设备的冷却水流量来进行控制。由于晶种分解过程具有大惯性、非线性、强干扰等特点,导致人工控制的分解温度误差大、波动大,远超过0.5 ℃,因此,实现晶种分解温度的准确控制成为实际生产中亟待解决的问题。
在以往的研究[6-9]中,晶种分解过程的建模多偏重于描述分解率或结晶粒度分布与其影响因素的关系,模型无法直接用于分解温度的控制,而揭示生产过程中分解温度与其影响因素之间关系的模型和分解温度自动控制方法尚未见报道。从工业实践中发展起来并已成功应用于过程控制领域的模型预测控制(MPC)方法是一种以模型预测、反馈校正和滚动优化为基本原理的实用控制算法,其闭环控制系统的性能主要取决于模型精度和干扰的特性。常规的MPC通过反馈校正对预测模型进行补偿,对于特性未知的不可测扰动的抑制能力较差[10]。目前,采用Kalman滤波器或Luenberger扰动观测器来估计扰动是提高MPC抗干扰性能的通用方法,研究[11-12]表明,在预测模型中添加合适的扰动动态信息能消除稳态偏差,但这些扰动估计方法都假设扰动分段恒定。MAEDER等[13]提出了对斜坡或震荡扰动信号进行估计的一般性方法,并给出了理论证明;但以上方法的扰动模型都是固定的,不足以描述时变的复杂扰动,SUN等[14]通过重估卡尔曼滤波器增益来更新扰动模型,这种方法需要扰动的协方差信息;徐祖华等[15]用自适应ARMA模型预测不可测扰动,并用多迭代伪线性回归方法对扰动模型进行辨识。在氧化铝晶种分解工序中,种分槽与外界环境的换热是降低分解温度的主要手段之一,天气变化对分解温度产生强烈影响,自然散热量也因此成为分解温度控制中的主要干扰因素之一,但种分槽与环境换热的机理复杂,影响散热量的某些变量(如风速和风向等)变化频繁且难以准确测量,无法建立准确的扰动机理模型[16]。本文作者针对氧化铝晶种分解过程的特点,提出了一种基于不可测干扰预测的NMPC控制方法(DP-NMPC),即采用机理分析与参数辨识相结合的方法建立晶种分解温度预测模型,利用时间序列分析方法对系统中因天气变化而产生的不可测扰动进行自适应估计,并利用估计结果对晶种分解温度预测模型进行实时校正。
1 氧化铝晶种分解工序
经过除杂精制的铝酸钠溶液在降至合适的分解初始温度后被泵入种分首槽,加入晶种的同时不断搅拌,混合后的分解浆料流经多个带机械搅拌的种分槽,逐渐冷却分解析出氢氧化铝结晶,此即晶种分解过程。该过程在常压下进行,种分槽内发生结晶放热反应,钢质的种分槽外壁直接与周围环境换热;槽内壁附近的提料筒内安装了检测槽内浆料温度的插入式温度计,顶部装配了宽流道板式换热器,槽中浆料由泵送至换热器,与来自循环水道的冷却水进行换热,冷却后的浆料返回种分槽,与槽内其他浆料混合;换热器冷热介质进出口处都有温度检测,冷却水进口管路有流量检测,并装备了可控制冷却水流量的电动阀门,以此控制种分槽内浆料的温度,即分解温度。种分槽系统能量传递过程如图1所示,图1中,F为流经种分槽物料的流量,m3/h;T为流出种分槽的分解浆料的温度,K;Tin为流入种分槽物料的温度,K;Fw为流经换热器冷却水的流量,m3/h;Fa为流经换热器的分解浆料的流量,m3/h;Tw,in、Tw,out分别为流入、流出换热器的冷却水温度,K;Ta,in、Ta,out分别为流入、流出换热器的分解浆料温度,K;ΔH为种分槽中单位时间内的反应焓变,J/h;Q为单位时间内自然散热带走的热量,J/h。
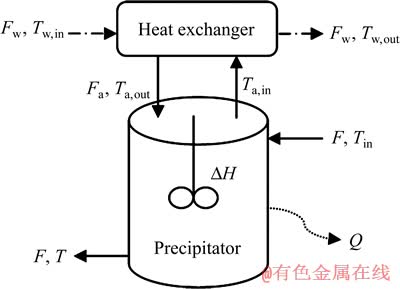
图1 种分槽系统能量传递过程示意图
Fig. 1 Schematic diagram of energy transfer process in a precipitator
2 种分槽系统建模
由热力学第一定律可得如式(1)和(2)所示的描述分解温度与冷却水流量关系的种分槽系统非线性模型,该模型由静态非线性函数和动态线性环节串联而成,具有Hammerstein模型结构,易于实施非线性预测控制。
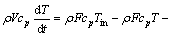
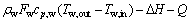 (1)
(1)
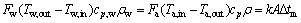 (2)
(2)
式中:ρ、ρw分别为分解浆料和冷却水密度,kg/m3;cp、cp,w分别为分解浆料和冷却水的定压比热容,J/(kg·K);A为换热器的总换热面积,m2;k 为换热器的总传热系数,J/(m2·K·h);Δtm为对数平均温差,K;t为分解时间,h;V为种分槽容积,m3。ΔH和Q无法直接测量,影响两者的变量也不能实时在线测量,因此,在系统建模时对其忽略不计,而作为不可测扰动由控制器进行抑制。由于种分槽系统中的强制换热过程达到平衡态的时间远小于种分槽系统的时间常数,所以可以利用静态模型描述该过程。在宽流道板式换热器中,冷、热介质几乎是全逆流流动,其对数平均温差为
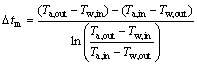 (3)
(3)
由式(2)和式(3)可得:
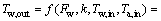
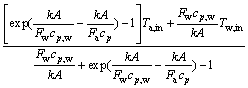 (4)
(4)
在实际生产过程中,换热面积和冷热介质的定压比热容都为常数,分解浆料侧的流量通常保持恒定,但换热器的总传热系数随工况不同而变化,由冷、热两侧的对流传热系数、换热板面的导热率及厚度决定,关系如下:
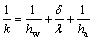 (5)
(5)
式中:hw为冷却水侧的对流换热系数,J/(m2·K·h);ha为分解浆料侧的对流换热系数,J/(m2·K·h);λ为换热器板片材料的导热系数,J/(m·K·h);δ为板片厚度,m。
根据传热相似理论,冷却水侧的对流换热准则关系可由如下方程表达:
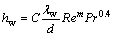 (6)
(6)
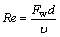 (7)
(7)
式中:C和m为待定系数;Re为冷却水侧雷诺数,反映流态对换热的影响;Pr为冷却水的普朗特数,仅与水的物性有关;λw为冷却水的导热系数,J/(m·K·h);d为冷却水侧的当量直径,m;υ为水的运动黏度,m2/s。
将式(6)、(7)代入式(5)可得:
 (8)
(8)
式中: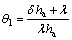 ,
,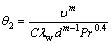 ,
,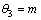 。
。
显然,不同工况下的待定系数θ1,θ2,θ3也不同,但在晶种分解过程中,冷、热两侧换热介质和换热器板片的物性参数随温度变化很小,且分解浆料侧的流量保持恒定,故换热器热侧的对流换热系数也基本恒定,因此,θ1、θ2和θ3基本恒定,可由相关生产数据辨识得到。
3 基于不可测扰动预测的自适应NMPC控制策略
晶种分解过程中,分解温度T为被控变量,冷却水流量Fw为操作控制变量,Tin、Tw,in和Ta,in为干扰变量。令y=T,u=Fw,v=Fw(Tw,out-Tw,in),d1=Tin,d2=Tw,in,d3=Ta,in,由种分槽系统模型可得分解温度的离散预测模型如下:
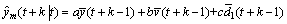 (9)
(9)
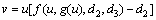 (10)
(10)
式中: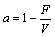 ,
,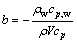 ,
,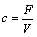 ,
,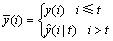 ,
,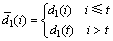 ,
,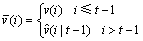 。
。
在预测模型中,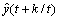 表示t时刻对变量y在t+k时刻的预测值,k≥0;
表示t时刻对变量y在t+k时刻的预测值,k≥0; 表示在t-1时刻对变量v在i时刻的预测值。
表示在t-1时刻对变量v在i时刻的预测值。
以上模型因无法预测天气变化等不可测强扰动对实际过程的影响而使常规的非线性预测控制性能降低,对此,本文作者提出一种改进的预测控制策略,通过对不可测扰动进行观测和预测来提高模型精度和控制性能。令d(t)为包括反应焓变、自然散热、测量误差等的等效总不可测扰动,通过分析种分槽系统模型可知,d(t)可由下式观测:
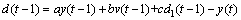 (11)
(11)
因能量传递过程存在较大惯性,d(t)的时间序列值之间必然存在具有某种统计规律的相互关系,通过建立描述这种统计规律的模型,可对d(t)序列进行预测。利用式(11)对实际种分过程进行观测得到的d(t)时间序列的自相关图和偏自相关图如图2所示,自相关图呈现出拖尾特性,而偏自相关图呈现出明显的2阶截尾特性,可见该序列为平稳随机序列,且可选择2阶自回归模型对其进行建模。
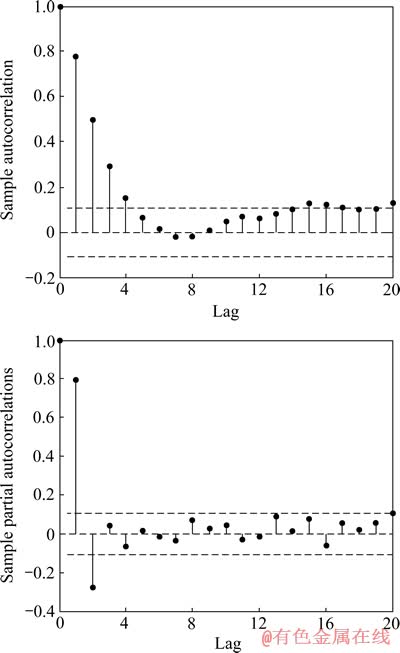
图2 观测扰动的时间序列自相关图和偏自相关图
Fig. 2 Autocorrelation (a) and partial autocorrelation (b) diagram of disturbances
不可测扰动的AR(2)模型如下:
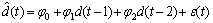 (12)
(12)
式中:ε(t)为零均值白噪声;φ0,φ1,φ2为模型参数,可由d(t)的历史观测值进行估计。每获得一个新的d(t)观测值,便重新估计模型参数,然后用新模型预测后续扰动,并以此修正线性预测子模型(9),修正后的预测输出为
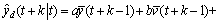
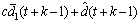 (13)
(13)
引入反馈校正后的预测输出为
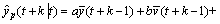
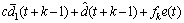 (14)
(14)
式中: ,fk为校正权值,是控制器的可调参数。
,fk为校正权值,是控制器的可调参数。
对于具有Hammerstein非线性结构的种分槽系统,本文作者采用计算量小、容易实施的两步法NMPC策略,即滚动求解如式(15)所示的线性子系统优化问题,得到当前最优中间控制变量v*(t)后,用数值求解非线性静态方程(10)并解饱和,即可得到当前最优操作控制变量uopt(t)。
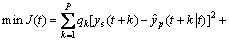
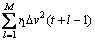 (15)
(15)
其中:ys为分解温度设定值;qk和rl分别表示误差权值和控制权值;P和M分别为预测时域和控制时域,四者均为预测控制器的设计参数。
两步法NMPC策略可在求解优化问题时不考虑约束,而在求解非线性方程时解饱和,因此可得到中间控制变量的解析解,求解式(15)的过程如下:
将多步预测模型中的历史测量值与未知操作变量进行分离,则预测模型的向量形式为
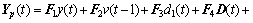
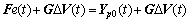 (16)
(16)
式中:
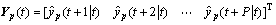
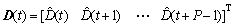
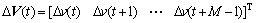
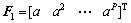
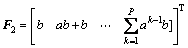
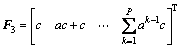

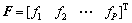

令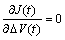 即可求出中间控制变量增量的解析解:
即可求出中间控制变量增量的解析解:
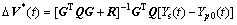 (17)
(17)
则当前最优中间控制变量为
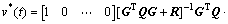
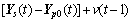 (18)
(18)
其中:Ys=[ys(t+1) ys(t+2) … ys(t+P)]T为设定值矩阵;Q=diag{q1, q2, …, qP},R=diag{r1, r2, …, rM},分别为误差权矩阵和控制权矩阵,由误差权值和控制权值组成。
基于不可测扰动预测的NMPC算法的实现步骤如下:
1) 离线计算F1、F2、F3、F4、G,初始化P、M、Q、R、F和采样时间等控制器可调设计参数,根据系统控制要求设定Ys;
2) 读入t时刻控制输入u(t-1)、中间输入v(t-1)、系统输出y(t)和可测扰动d1(t)、d2(t)、d3(t);
3) 由式(11)观测d(t-1),更新自回归模型式(12)中的参数,由更新后的模型式(12)预测后续扰动d(t+k-1),得到D(t);
4) 计算e(t),并由式(16)计算出Yp0(t);
5) 由式(18)计算出v*(t)后,数值求解式(10)并解饱和得到uopt(t);
6) 执行uopt(t),令t=t+1,转入步骤(2)。
4 仿真研究及分析
选取某氧化铝厂的带板式换热器的种分槽系统作为仿真实验对象,晶种分解过程运行于表1所示工作点附近。本文作者采用该厂2011年10月的实际生产数据辨识了待定系数θ1,θ2,θ3,并由式(4)和式(8)计算出11月换热器冷侧的出口温度,模型计算温度与实际测量温度的对比如图3所示,仿真曲线与测量值吻合良好,两者的Theil不等系数[17]为0.022,该值越接近0表示两条曲线越一致,证明本静态换热器模型能准确描述实际换热过程。由种分槽系统模型计算出的分解温度和现场实测的分解温度的对比如图4所示,两者的Theil不等系数为0.24,可见该模型虽能基本准确地描述实际过程,但因忽略了实际过程中的反应焓变和自然散热等因素,导致模型输出与实际过程存在误差。
表1 模型参数
Table 1 Model parameters

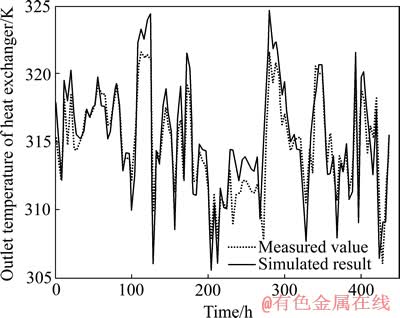
图3 换热器静态模型仿真曲线
Fig. 3 Simulation result of heat exchanger static model
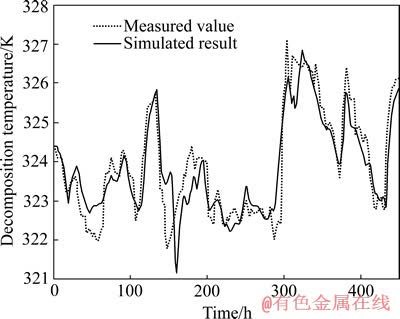
图4 种分槽系统动态模型仿真曲线
Fig. 4 Simulation result of precipitator system dynamic model
种分温度的控制仿真系统均采用2011年11月的包含了真实扰动和噪声的实际生产数据作为输入数据,这些数据没有进行任何滤波降噪处理,采样时间为1 h,控制器参数P=12,M=2,qk=1,rl=0.01。分别采用常规NMPC控制方法和本文提出的DP-NMPC控制方法对种分槽系统进行控制仿真,两种方法的闭环控制系统阶跃响应比较如图5所示,设定值从324.4 K跃变至325.4 K,其中常规NMPC方法跟踪设定值的均方误差为0.174,采用本方法的均方误差为0.058。
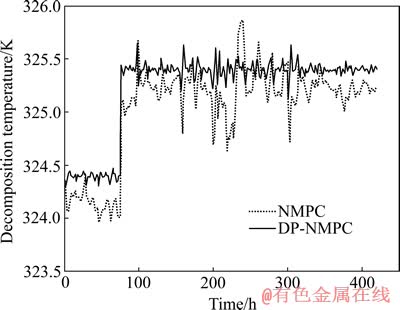
图5 NMPC控制系统与DP-NMPC控制系统的阶跃响应
Fig. 5 Step response of NMPC and DP-NMPC control system
由图5可知,常规NMPC方法存在明显的稳态误差,在强干扰作用下受控分解温度波动剧烈,而DP-NMPC方法的稳态控制精度高,有较强的抗干扰能力,能使受控分解温度在-0.5~0.5 K的范围内围绕设定值波动,且超调较小,其原因在于本方法在预测模型中引入了对不可测扰动的自适应预测,提高了模型的精度和系统的抗干扰能力。可见,本方法能快速跟踪系统设定值,较好地抑制超调,抗干扰能力更强,控制性能相比常规NMPC明显提高,能满足晶种分解生产过程中对分解温度的控制要求。
5 结论
1) 将机理分析与参数辨识相结合,建立了描述氧化铝晶种分解工序中带板式换热器的种分槽系统的非线性动态模型。该模型由静态非线性函数和动态线性环节串联而成,具有Hammerstein模型结构,易于采用非线性预测控制技术,实际生产过程数据验证了模型的正确性。
2) 针对氧化铝晶种分解过程具有的大惯性、非线性、强干扰特点,提出了一种基于不可测干扰预测的NMPC控制方法。该方法利用时间序列分析方法建立系统中不可测扰动的自适应预测模型,并以此对晶种分解温度模型进行校正,同时保留了MPC原有的反馈校正机制,提高了晶种分解温度模型的准确性和对工况的适应能力。
3) 基于实际生产过程数据的仿真研究表明,相比常规NMPC,本方法提高了控制模型的精度,使控制系统能快速跟踪系统设定值,更好地抑制超调,抗干扰能力更强,能对晶种分解温度进行有效控制。
4) 本方法适用于具有不可测非白噪声强干扰过程的模型预测控制,具有显著的实用价值。
REFERENCES
[1] 许国栋, 敖 宏, 佘元冠. 可持续发展背景下世界铝工业发展现状、趋势及我国的对策[J]. 中国有色金属学报, 2012, 22(7): 2040-2051.
XU Guo-dong, AO Hong, SHE Yuan-guan. Current status and development trend of aluminum industry in world and strategy suggestions in China under background of sustainable development[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(7): 2040-2051.
[2] 尹周澜, 刘吉波, 张平民, 陈启元, 李 洁. 氧化铝生产种分过程Rpeq的测定及其与降温制度的关系[J]. 中国有色金属学报, 2001, 11(6): 1136-1139.
YIN Zhou-lan, LIU Ji-bo, ZHANG Ping-min, CHEN Qi-yuan, LI Jie. Measurement of Rpeq in practical precipitation process of alumina refinery and relation of Rpeq with temperature-drop program[J]. The Chinese Journal of Nonferrous Metals, 2001, 11(6): 1136-1139.
[3] 陈国辉, 陈启元, 尹周澜, 张 斌, 李 洁, 陈金清, 刘吉波. 超声强化和温度对铝酸钠溶液种分过程的影响[J]. 中国有色金属学报, 2002, 12(3): 607-610.
CHEN Gou-hui, CHEN Qi-yuan, YIN Zhou-lan, ZHANG Bin, LI Jie, CHEN Jin-qing, LIU Ji-bo. Fractal kinetics study on precipitation of sodium aluminate liquor under ultrasound[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(3): 607-610
[4] 洪利明, 刘晓作, 任凤莲, 王超男, 沈祥会,. 铝酸钠溶液种分过程降温制度的研究[J]. 有色金属, 2010, 2: 31-34.
HONG Li-ming, LIU Xiao-zuo, REN Feng-lian, WANG Chao-nan, SHEN Xiang-hui. Study of decreasing temperature on seed precipitation of sodium aluminate solution[J]. Nonferrous Metals, 2010, 2: 31-34.
[5] 张家元, 李永清, 付明辉, 刘 斌, 李 黎. 氧化铝种分过程浓度及质量比模型的研究[J]. 中南大学学报: 自然科学版, 2011, 42(6): 1543-1548.
ZHANG Jia-yuan, LI Yong-qing, FU Ming-hui, LIU bin, LI Li. Concentration and mass ratio model of gibbsite precipitation process in alumina[J]. Journal of Central South University: Science and Technology, 2011, 42(6): 1543-1548.
[6] WU Yu-sheng, ZHANG Di, LI Ming-chun, BI Shi-wen, YANG Yi-hong. Periodical attenuation of Al(OH)3 particles from seed precipitation sodium aluminate solution[J]. Chinese Journal of Nonferrous Metals, 2010, 20(3): 528-532.
[7] 尹建国, 李旺兴, 尹中林, 陈启元, 尹周澜, 苏赵辉. 种分聚附过程中氢氧化铝粒度分布的振荡曲线[J]. 中国有色金属学报, 2009, 19(4): 738-743.
YIN Jian-guo, LI Wang-xing, YIN Zhong-lin, CHEN Qi-yuan, YIN Zhou-lan, SU Zhao-hui. Oscillation curves of particle size distribution of aluminum hydroxide in seeded agglomeration process[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(4): 738-743.
[8] 张家元, 李永清, 付明辉, 刘 斌. 氧化铝种分过程粒度分布的动态模型[J]. 中南大学学报: 自然科学版, 2009, 40(4): 799-883.
ZHANG Jia-yuan, LI yong-qing, FU Ming-hui, LIU Bin. Particle distribution dynamic model of gibbsite precipitation process during alumina production[J]. Journal of Central South University: Science and Technology, 2009, 40(4): 799-883.
[9] LI Xiao-bin, LIU Zhi-jian, XU Xiao-hui, ZHOU Qiu-sheng, PENG Zhi-hong, LIU Gui-hua. Model of apparent crystal growth rate and kinetics of seeded precipitation from sodium aluminate solution[J]. Journal of Central South University of Technology, 2005, 12(6): 662-666,
[10] QIN S J, BADGWELL T A. A survey of industrial model predictive control technology[J]. Control Engineering and Practice, 2003, 11: 733-764.
[11] HUUSOM J K, POULSEN N K, JORGENSEN S B, JORGENSEN J B. Tuning SISO offset-free model predictive control based on ARX models[J]. Journal of Process Control, 2012, 22: 1997-2007.
[12] WALLACE M, DAS B, MHASKAR P, HOUSE J, SALSBURY T. Offset-free model predictive control of a vapor compression cycle[J]. Journal of Process Control, 2012, 22: 1374-1386.
[13] MAEDER U, MORARI M. Offset-free reference tracking with model predictive control[J]. Automatica, 2010, 46: 1469-1476.
[14] SUN Zhi-jian, QIN S J, SINGHAL A, MEGAN L. A novel MPC strategy by adapting disturbance models[C]// AIChE Annual Meeting. Nashville, TN, 2009.
[15] XU Zu-hua, ZHU Yu-cai, HAN Kai, ZHAO Jun, QIAN Ji-xin. A multi-iteration pseudo-linear regression method and adaptive disturbance model for MPC[J]. Journal of Process Control, 2010, 20: 384-395.
[16] 刘 征, 彭小奇. 氧化铝晶种分解能量传递过程的动态建模[J]. 中南大学学报: 自然科学版, 2013, 44(3): 1037-1042.
LIU Zheng, PENG Xiao-qi. Dynamic modeling for energy transfer process in alumina precipitation[J]. Journal of Central South University: Science and Technology, 2013, 44(3): 1037-1042.
[17] 康凤举. 现代仿真技术与应用[M]. 北京: 国防工业出版社, 2006: 351-352.
KANG Feng-ju. Modern simulation technology and application[M]. Beijing: National Defense Industry Press, 2006: 351-352.
(编辑 龙怀中)
基金项目:国家自然科学基金重点项目(61134006);国家自然科学基金面上项目(61273169);国家自然科学基金青年项目(61105080)
收稿日期:2012-07-20;修订日期:2013-04-15
通信作者:彭小奇,教授,博士;电话:0731-88836713;E-mail: pengxq@csu.edu.cn