变增益PI速度控制器在间接磁场定向控制系统中的应用
李建军1, 2，桂卫华1，张超1，何亚屏1，盛洁波2
(1. 中南大学 信息科学与工程学院，湖南 长沙，410075；
2. 湖南工学院 电气与信息工程系，湖南 衡阳，421002)
摘 要：针对感应电机无速度传感器间接磁场定向控制系统中传统PI控制器和磁通观测器的不足，利用感应电机的时变参数模型的降阶处理方法，提出一种变增益的PI速度控制器；为获得无速度传感器控制，提出一种非线性鲁棒高增益观测器。仿真和试验验证表明：PI速度控制器不但能根据实际工况实现PID参数的在线调整，而且工程实现简单，减少了系统在启动阶段的超调；非线性鲁棒高增益观测器只需要电机的定子电压和电流，能同时观测电机的状态量和转子时间常数等参数，鲁棒性好，计算量少，易于适时在线实现。
关键词：感应电机；间接磁场定向控制；高增益观测器；变增益PI控制器
中图分类号：TP391.9 文献标志码：A 文章编号：1672-7207(2010)02-0615-08
A variable gain PI controller used for speed control of induction motor IDFOC system
LI Jian-jun1, 2, GUI Wei-hua1, ZHANG Chao1, HE Ya-ping1, SHENG Jie-bo2
(1. School of Information Science and Engineering, Central South University, Changsha 410075, China;
2. Department of Electric and Information Engineering, Hunan Institute of Technology, Hengyang 421002, China)
Abstract: Based on the reduced order of the IM model of the sensor-less indirect field oriented control (IDFOC) system, a simple variable gain PI speed controller was presented. In order to implement the sensor-less control, a high gain observer (HGO) was proposed to estimate the rotor fluxes, speed and time constant using the stator currents and voltages. Simulation and experimental results show that the proposed method can adjust the PID parameters online, the engineering implementation is very easy, and the speed overshot decreases during the startup. HGO has many advantages, such as good robustness, less computation, and real time identification of the IM.
Key words: induction motor (IM); indirect field oriented control (IDFOC); high gain observer (HGO); variable gain PI controller (VGPI )
在感应电机的矢量控制中，关键要确定转子磁通和转子速度。对无速度传感器控制系统，磁通和转速的获得一般是通过可测量的定子电压和电流，利用观测器理论实现[1]。然而，感应电机本质上是1个强耦合的非线性系统，许多学者对其参数估算进行了研究，也提出了许多实用的方法[2-3]，如Beguenane等[4]提出了1种模型参考自适应(MRAS)方法，该方法简单，但是，对电机参数很敏感。Lee等[5]提出了一种扩展卡尔曼滤波(EKF)方法，该方法是1种随机观测器，系统的非线性在取样时间内被线性化，它最大的优点就是能同时观测状态和系统参数，但是，计算量大，鲁棒性不高。同时，还有Extended Luenberger Observer (ELO)方法[6-7]和滑模控制方法[8]等。近年来，大量的智能控制方法也引入了电机的控制领域，如神经网络、模糊控制等[9-10]，这些方法给系统带来了较大的计算量，控制效果也有许多局限性。Moreno等[11-12]提出了1种高增益观测技术(HGO)，可以同时辨识系统的状态和参数，且对微处理器的要求不高，计算机适时实现也很简单。
本文作者在文献[12]的基础上，利用HGO技术，针对感应电机无速度传感器控制系统，提出了一种非线性鲁棒观测器，观测器利用电机的时变参数模型，只需要电机定子电流和电压，利用电机的降阶模型来获得对电机参数的适时辨识，以实现电机的磁场定向控制(IDFOC)。在无速度传感器控制系统中，速度控制器一般是PI控制器[13]，固定参数的PI控制器虽然结构简单，方便实现，但是对过程变化敏感。为克服这一缺点，一般是引入智能控制，如模糊控制[14-17]等，利用智能控制在线调整其系数，但是无形中增加了系统的复杂性。本文作者在得到同步旋转坐标系下的转子磁场定向的感应电机状态空间描述方程的基础上，设计出感应电机的高增益观测器(HGO)对电机参数和状态进行观测，利用观测得到的参数，设计出速度的变增益PI(VGPI)控制器。该方法简单，不但能实现了PID参数的在线调整，而且能有效克服系统在启动时的超调等不良效果，工程实现简单。
1 感应电机模型及其IDFOC原理
1.1 感应电机的数学模型
在同步旋转d-q坐标下的感应电机方程的状态空间描述为[12]：
(1)
式中：
，
，
；
，为定子电压；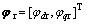
，为转子磁通；
，为定子电流；p为电机极对数；Tr=Lr/Rr，为转子时间常数；Ls和Lr分别为电机定子电感和转子电感；J为电机转动惯量；Tl为负载力矩；f为摩擦因数；M为电机互感；ωs，ωr和ωsl分别为定子速度、转子速度和转差速度；Rs和Rr分别为定子电阻和转子电阻；pN为电机额定功率。
1.2 间接转子磁场定向
根据矢量控制的基本原理[12]，按转子磁场定向，满足：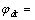
，
。这样，电机的电磁力矩等式变为：
(2)
从而可以把交流电机等效为一个直流电机。
电压方程为：
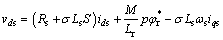(3)
(4)
式中：
为的参考值；S为拉氏算子。
磁场定向角为：
(5)
2 高增益观测器原理
对一非线性系统：
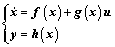(6)
其中：x∈Rn；u∈Rm；y∈Rl。
约定系统(6)可观测，则存在一线性变换z=G(x)，使原系统变换为：
(7)
建立如下观测器[18-19]：
(8)
式中：A为系统矩阵，C为系统输出矩阵；
为观测器状态；K为观测增益；
的定义见文献[18]。
在式(8)中，选择K使A-KC稳定，
为下述 Lyapunov 方程(9)的解：
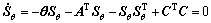(9)
其中：G∈Rn×n；g设计为足够大的正数。
再通过逆变换到原来变量，得到原系统(6)的观测器为：
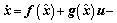
(10)
(11)
其中：
为Lie导数[18]；
；
；
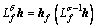为相应观测器。
本观测器的指数收敛性已经在文献[18]进行了证明，高增益观测器HGO的设计重点就是计算出：
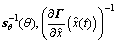
3 HGO在感应电机中的应用
3.1 感应电机的HGO模型
对感应电机的控制，一般要确定其转子磁通和角速度，把式(2)所示的感应电机的模型写成式(6)的形式，其中：
，为状态变量，
，为输出变量，
，为控制输入量。
(12)
(13)
(14)
相应地解等式(9)~(11)，可得：
(15)
(16)
式中：
，
，
分别为相应量
，
，
的观测值。
3.2 转子时间常数观测
根据模型(2)，为了简化设计，需对原模型进行降阶。选
为输入量，把电压模型开环观测得到的转子磁通作为输出量：
，状态量为：
，
。利用HGO原理，对其进行观测，得到：
(17)
(18)
式中：
为相应的观测值。
3.3 开环磁通观测
为简化计算，对观测转子时间常数所需要的磁通，利用基于电压模型的感应电机磁通开环观测器得到：
(19)
基于电压模型的磁通观测器中，由于存在纯积分，使得系统在低速度时的性能不稳定，特别是对参数的变化敏感性很大[13]。但是，观测器的状态是转子磁通和时间常数，一方面，减少了计算量和计算的复杂性，另一方面，在低速时，转子时间常数很容易被观测到。只要转子时间常数足够准确，就可以实现电机磁通和力矩间的良好动态解耦，从而可以获得快速、准确的力矩控制。
4 速度变增益控制器的设计
4.1 VGPI控制器的基本原理
速度控制器采用变增益PI(VGPI)控制器，整个系统的结构如图1所示。
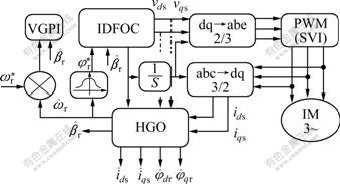
图1 系统结构图
Fig.1 System schematic structure
控制器的数学描述为：
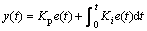(20)
其中：e(t)为控制器的输入；y(t)为VGPI控制器的输出。其参数整定原理见图2。其中：
(21)
(22)
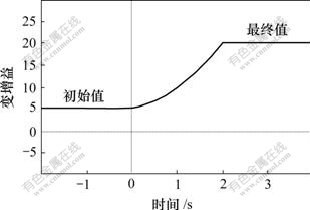
图2 变增益PI参数整定曲线
Fig.2 Variable PI gain tuning curve
暂态多项式的维数n定义为VGPI的维数。选Ki的初始值为0。
变增益PI控制器需要调整4个参数[17]：
(1) 增益初始值，主要消除启动时候的超调。
(2) 增益稳态值，主要克服快速的负载干扰。
(3) 增益动态函数，是一多项式函数，满足从初始到稳态的动态要求。
(4) 饱和时间，控制器从初始到最终稳态值所需要的时间，Ts即为饱和时间。
为了选择1个恰当的维数，先求得VGPI的单位阶跃响应为：
(23)
n和y(t)的关系曲线如图3所示。当n=0时，控制器是一般的PI控制器。在暂态区域(t＜Ts)，一般的PI控制器是起始于Kpf，终止于Kpf+TsKif的一个线性过程。
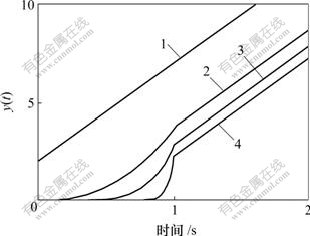
维数n：1—0; 2—2; 3—5; 4—20
图3 VGPI控制器在维数n不同时的阶跃相应曲线
Fig.3 VGPI step response for different degrees
而对VGPI控制器，起阶跃响应(n≠0)按照起始Kpi，终止于Kpf+TsKif/(n+1)的n+1维多项式曲线变化。在稳态区(t＞Ts)，2种控制器都是具有斜率Kif的线性函数。从而可以看出：VGPI控制器和一般的PI控制器都具有相同的稳态性能，但是，VGPI控制器在动态过程中比一般PI控制器对阶跃有较大的阻尼，可以克服动态过程中的超调。
4.2 VGPI控制器参数的动态整定
为确定VGPI控制器参数，按以下方法进行整定：
(1) 假设n=1，为了克服负载扰动，选择1个较大的Kif和1个恰当的Ts。
(2) 按照减少速度超调的原则决定Kpi和Kpf。
(3) 若不能有效抑制速度超调，则不断调整Ts，不断重复以上步骤，直到满意为止。
(4) 若通过增大Ts不能达到要求，则增加n，直到满意为止。
这里，速度控制器参数为：
；
；n=3；Kpi初始值通过仿真动态获得。其中：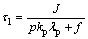
；
。
通过上面的理论分析以及在仿真实验中的调节，本文设计的变增益PI调节器的数学方程为：
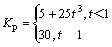(24)
(25)
为达到与普通PI调节器在稳态时同样的调节效果，变增益PI调节器的终值采用普通PI调节器的终值：Kp=30；Ki=1。
5 仿真与试验
5.1 仿真结果
基于变增益PI控制器的无速度传感器矢量控制系统采用的感应电机仿真参数如表1所示。
表1 感应电机参数
Table 1 Induction machine parameters
图4和图5所示分别是采用变增益PI调节器和一般PI调节器时速度阶跃变化的仿真结果，其中：速度在1 s时从1 200 r/min阶跃变化至600 r/min，给定负载转矩为400 N?m，转子时间常数为正常值。从图5可以看出：当采用一般PI速度调节器时，在1 s时速度阶跃变化时的速度估计曲线和实际曲线进入稳态时间较长，且电磁转矩曲线在开始时刻抖动很大。从图4可以看出：在起始时刻采用VGPI调节器的速度估计曲线和电磁转矩曲线的效果均明显优于采用一般的PI调节器的效果。
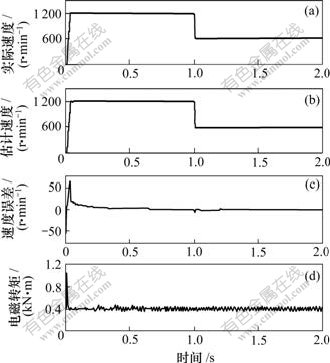
(a) 实际速度；(b) 估计速度；(c) 速度误差；(d) 电磁转矩
图4 采用VGPI控制器速度阶跃变化时速度辨识及
转矩仿真结果
Fig.4 Speed identification and torque simulation results with a VGPI controller at a step speed
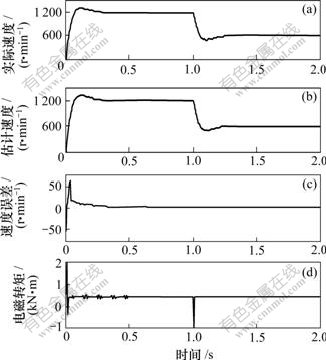
(a) 实际速度；(b) 估计速度；(c) 速度误差；(d) 电磁转矩
图5 采用普通PI控制器速度阶跃变化时速度辨识及
转矩仿真结果
Fig.5 Speed identification and torque simulation results with PI controller at a step speed
图6所示为采用VGPI控制器，1 s时给定速度从1 200 r/min变化到600 r/min以及给定转矩在2 s时从100 N?m阶跃变化到400 N?m时的仿真结果。从图6可以看出：速度估计曲线和实际参考曲线超调量很小，且速度估计误差在0.6 s左右稳定至0 r/min，转子时间常数观测曲线也能很好地跟踪实际参考曲线。在2 s时给定负载转矩阶跃变化对采用高增益观测器的速度估计以及转子时间常数观测曲线几乎没有影响。
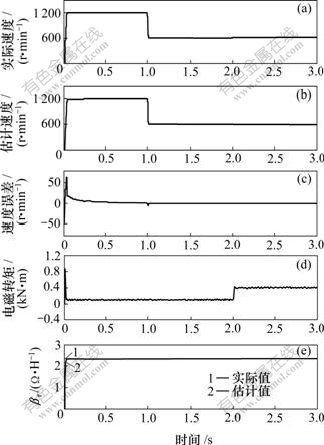
(a) 实际速度；(b) 估计速度；(c) 速度误差；
(d) 电磁转矩；(e) 转子时间常数
图6 采用VGPI控制器在2 s时给定转矩阶跃变化时的
仿真结果
Fig.6 Simulation results with a VGPI controller at t=2 s and a step torque
感应电机的间接磁场定向控制系统对转子时间常数比较敏感，而转子时间常数的变化主要是由转子电阻随温度变化引起的[20]，转子时间常数的倒数为βr=Rr/Lr，当转子电阻随温度变化为原来的1.5倍时，相当于βr变为原来的1.5倍。
图7所示为采用VGPI控制器，1 s时转子时间常数的倒数从常值2.331 9阶跃变化到其值的1.5倍以及2 s时速度从1 200 r/min变化到600 r/min时的仿真结果。从图7可以看出：转子时间常数观测曲线能很好地跟踪实际转子时间常数曲线，且对速度辨识影响较小，电磁转矩曲线也仅在1 s时转子时间常数阶跃变化和2 s时刻速度阶跃变化时有点抖动。从以上的仿真结果可知：基于高增益观测器的速度及转子时间常数辨识方案能够很好地实现速度和转子时间常数辨识，且对负载转矩的变化有一定的鲁棒性，同时，本文设计的变增益控制器(VGPI)比一般的PID控制器具有更加优越的性能，能够很好消地抑制速度超调以及负载转矩的抖动。
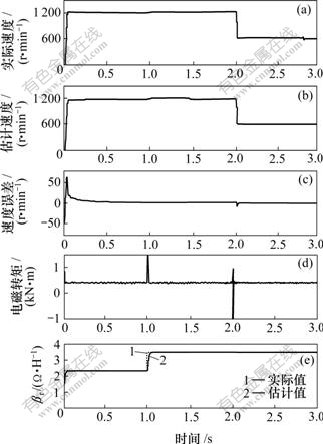
(a) 实际速度；(b) 估计速度；(c) 速度误差；
(d) 电磁转矩；(e) 转子时间常数
图7 采用VGPI控制器在1 s时转子时间常数阶跃变化时的仿真结果
Fig.7 Simulation results with a VGPI controller at t=1 s and a time constant step
5.2 实验验证
本文设计的变增益PI控制器感应电机间接磁通定向控制方案已经通过实验验证，整个实验装置包括300 kW的感应电机1台，电压源逆变器以及控制装置1台，控制装置由1块浮点DSP(TM320C31)和1块定点DSP(TM320F240)组成。速度辨识和VC控制在TM320C31上实现，为了得到比较效果，使用脉冲编码器由TM320F240通过M/T法获得实际速度。为了获得精确的速度辨识结果并使控制系统保持较好的动态性能，使用低通滤波器适当补偿逆变器电压降并阻止高频型号通过变增益PI控制器。
图8和图9所示为感应电机采用变增益PI(VGPI)情况下的转子磁通、速度和电磁转矩实验结果，其中：1 s时给定速度从1 200 r/min变化到600 r/min，给定转矩为400 N?m，转子时间常数的倒数为其值的1.5倍。转子磁通d轴分量最终稳定在0.96 Wb，由于采用转子磁场定向，转子磁通q轴分量为0 Wb，磁链曲线与理论分析基本一致。从图9可以看出：电机的估计速度能够很好地跟踪电机实际参考速度，而且电机启动阶段超调量很小，电磁转矩在启动时脉动较小，在速度发生阶跃变化时对其有点影响外，能够很好地稳定在400 N?m。
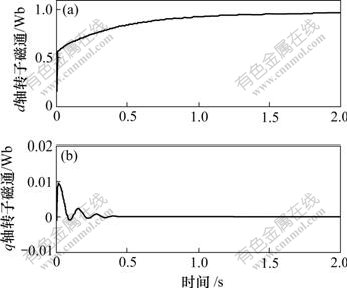
(a) 转子磁通d轴分量；(b) 转子磁通q轴分量
图8 采用VGPI控制器时的转子磁通的实验结果
Fig.8 Experiment results of rotor flux with VGPI controller
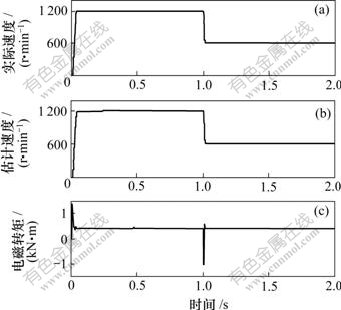
(a) 电机实际参考速度；(b) 电机估计速度；(c) 电磁转矩
图9 采用VGPI控制器、速度阶跃变化时的实验结果
Fig.9 Experiment results of rotor flux with a VGPI controller at a step speed
图10所示为异步电动机采用变增益PI控制器。当转子时间常数的倒数为其值的1.5倍、给定速度为 1 200 r/min、给定转矩在1 s时从100 N?m阶跃变化到400 N?m时的速度辨识以及电磁转矩实验曲线。从图10可以看出：电磁转矩发生阶跃变化对转速的辨识效果并不产生明显的影响，电机的估计速度与电机的实际参考速度基本相同，因此，估计速度也能很好地跟踪实际参考速度。由此可知，本文提出的能抑制速度超调以及负载转矩的抖动的变增益控制器(VGPI)方案是切实可行的。
(a) 电机实际参考速度；(b) 电机估计速度；(c) 电磁转矩
图10 采用VGPI控制器、转矩阶跃变化时的实验结果
Fig.10 Experiment results of rotor flux with a VGPI controller at a step torque
6 结论
(1) 对目前IDFOC系统中使用90%以上的PI控制器进行了改进，提出了一种变增益PI控制器，其增益可以根据实际工况实现在线调整，从而提高了系统的鲁棒性能，克服了传统PI控制器的一些不足。
(2) 为实现无速度传感器控制，引入高增益观测器，适时对感应电机的状态和时间常数进行观测，从而获得了感应电机的间接磁场准确定向，提高了系统整体解耦性能。
(3) 所提出的技术工程实现简单，性能可靠。
参考文献：
[1] Abdellah M, Chenafa M, Bouhenna A, et al. Powerful nonlinear observer associated with field-oriented control of an induction motor[J]. Int J Appl Math Comput Sci, 2004, 14(2): 209-220.
[2] Alamir M. Sensitivity analysis in simultaneous state parameter estimation for induction motors[J]. International Journal of Control, 2002, 75(10): 753-758.
[3] Jeon S H, Oh K K, Choi J Y. Flux observer with online tuning of stator and rotor resistances for induction motors[J]. IEEE Trans Ind Electron, 2002, 49(3): 653-664.
[4] Beguenane R, Ouhrouche M. MRAC-IFO induction motor control with simultaneous velocity and rotor-inverse time constant estimation[C]//Proc of the IASTED Int Conf PES’. California: Palm Springs, 2003: 465-470.
[5] Lee C M, Chen C L. Speed sensorless vector control of induction motor using Kalman-filter-assisted adaptive observer[J]. IEEE Trans Ind Electron, 1998, 45(2): 359-361.
[6] Lee C M, Chen C L, Lee K B, et al. Reduced-order extended Luenberger observer based sensorless vector control driven by matrix converter with nonlinearity compensation[J]. IEEE Trans Ind Electron, 2006, 53(1): 66-75.
[7] Sbita L, Ben Hamed M. An MRAS based full order Luenberger observer for sensorless DRFOC of induction motors[J]. Int J ACSE, 2007, 7(1): 11-20.
[8] Kim S M, Han W Y, Kim S J. Design of a new adaptive sliding mode observer for sensorless induction motor drive[J]. Elec Power Syst Res, 2004, 70(1): 16-22.
[9] Kenne G, Ali T A, Lagarrigue F L, et al. Nonlinear systems parameters estimation using radial basis function network[J]. Control Eng Pract, 2006, 14(7): 819-832.
[10] Sbita L, Ben H M. Fuzzy controller and ANN speed estimation for induction motor drives[C]//IEEE Forth Int Multi-Conf on Systems, Signals and Devices. Piscataway: IEEE, 2007: 19-22.
[11] Moreno J, Vargas A. Approximate high-gain observers for uniformly observable nonlinear systems[C]//Proc 39th IEEE Conf on Decision and Control. Piscataway: IEEE, 2000: 784-789.
[12] Messaoudi M, Sbita L, Abdelkrim M N. On-line rotor resistance estimation for sensorless indirect vector control of induction motor drives[C]//IEEE Forth Int Multi-Conf on Systems, Signals and Devices. Piscataway: IEEE, 2007: 19-29.
[13] Varghese G C, Sanders S R. Observers for flux estimation in induction machines[J]. IEEE Trans Ind Electron, 1998, 35(1): 85-94.
[14] 奚国华, 张艳存, 胡卫华, 等. 基于模糊DSVM控制策略的异步电机直接转矩控制[J]. 中南大学学报: 自然科学版, 2008, 39(1): 166-171.
XI Guo-hua, ZHANG Yan-cun, HU Wei-hua, et al. Direct torque control of induction motors based on fuzzy DSVM strategy[J]. Journal of Central South University: Science and Technology, 2008, 39(1): 166-171.
[15] Miloudi A, Draou A. Variable gain PI controller design for speed control and rotor resistance estimation of an indirect vector controlled induction machine drive[C]//Conference Record of the IECON’02. Piscataway: IEEE, 2002: 323-328.
[16] Miloudi A. Radadi A, Draou A, et al. Simulation and modeling of a variable gain PI controller for speed control of a direct torque neuro fuzzy controlled induction machine drive[C]//Conf Rec PESC’04. Piscataway: IEEE, 2004: 20-25.
[17] Miloud A, Eid A, Radadi A, et al. A variable gain PI controller used for speed control of a direct torque neuro fuzzy controlled induction machine drive[J]. Turk J Elec Engin, 2007, 15(1): 37-49.
[18] Besancon G, Zhang Q H, Hammouri H. High gain observer based state and parameter estimation in nonlinear systems[C]//15th World Congress IFAC. Stuttgart: Institute fur Systemtheorie, 2002.
[19] Bornard G, Hammouri H. A high gain observer for a class of uniformly observable systems[C]//Proc 30th IEEE Conf on Decision and Control. New York: IEEE, 1991: 122-991
[20] Mouna B H, Lassaad S. Speed sensorless indirect stator field oriented control of induction motor based on Luenberger observer[C]//2006 IEEE International Symposium on Industrial Electronics. Piscataway: IEEE, 2006: 2473-2478.
收稿日期：2009-01-23；修回日期：2009-04-17
基金项目：湖南省教育厅科技项目(06C042)；国家自然科学基金重点资助项目(60634020)；湖南工学院院级科研项目(HY08026)
通信作者：李建军(1968-)，男，湖南衡阳人，教授，从事非线性控制、电气传动控制的研究；电话：13875793910；E-mail: hgljj68@163.com
(编辑 赵俊)
