文章编号：1004-0609(2013)07-1892-08

韧性材料的微裂纹扩展和连通的晶体相场模拟

高英俊^{1, 2}，罗志荣¹，黄礼琳¹，林  葵¹

(1. 广西大学  物理科学与工程技术学院，南宁530004；

2. 中国科学院  国际材料物理中心，沈阳110016)

摘  要：采用晶体相场模型研究韧性单晶材料在双轴拉伸条件下微裂纹扩展和连通的演化过程，分析应变、初始裂口处原子密度等因素对裂纹扩展和分叉的影响。结果表明：初始裂口处原子密度对裂纹扩展有明显的影响；对于双轴拉伸作用，当应变较小时，裂纹扩展不分叉；当应变较大时，裂纹扩展才能出现分叉。在裂纹扩展过程中，体系能量不断降低；当裂纹出现分叉时，体系能量降低更快，这表明裂纹扩展过程中弹性应变能的释放比表面能的增加要快。裂纹在扩展过程中，在分叉处会出现与主裂纹断开的孤立的微小空洞。这些微小空洞将成为新的裂纹萌生之地，它们在应力的作用下不断长大，连成一线，形成新的裂纹分支。同一条直线上的两条初始裂纹在扩展过程中，当裂纹尖端靠近时，尖端相互吸引，裂纹相互连通。本研究所得结果与相关模拟结果和实验结果吻合。

关键词：晶体相场模型；微裂纹扩展；应变；韧性材料

中图分类号：TG111.5           　   　     文献标志码：A

Phase-field-crystal modeling for microcrack propagation and connecting of ductile materials

GAO Ying-jun^{1, 2}, LUO Zhi-rong¹, HUANG Li-lin¹, LIN Kui¹

(1.College of Physics Science and Engineering, Guangxi University, Nanning 530004, China;

2.International Center for Materials Physics, Chinese Academy of Science, Shenyang 110016, China)

Abstract: The morphology evolution of microcrack propagation and connecting in ductile single crystal materials under the biaxial tensile deformation were simulated by the phase-field-crystal model. The effects of the factors such as the stain, the atomic density in initial crack notch on crack propagation were analyzed. The simulation results show that the atomic density in the crack notch has an effect on crack propagation. As the tensile strain exerting on the monocrystalline sample by biaxial tensile, the crack propagation cannot branch at small strain, the first-branching and second-branching occur during crack propagation when the strain is great enough. It is observed that system energy decreases over time and the energy decreases faster during crack branching. It indicates that the decrease in elastic strain energy is larger than the increase in surface energy during crack propagation. A string of isolate cavities near main cracks can be seen and these cavities will become new cracks with time lasting during crack propagation. They will continue to grow up along a line and become a new branch crack under the stress. The tips of two initial cracks on the same line would attract each other during crack propagation, once they made the connection, the two cracks would form into one. The simulation results are in agreement with other simulation results and experimental ones.

Key words: phase-field-crystal model; microcrack propagation; strain; ductile materials

材料在介观和宏观尺度上的性能很大程度上由复杂的拓扑几何缺陷所决定，例如空位、空洞、位错、晶界和微裂纹等。这些缺陷起源于在原子尺度发生的复杂非平衡动力学过程。就目前所采用的多尺度模拟方法来说，对这些微观特征结构的实时演化过程的建模和模拟是一个重大挑战。相场方法是当今研究微观结构演化的强有力的数值计算方法^[1-2]。传统的相场方法^[3-8]是建立在平衡态均匀场基础上的，忽略了许多由原子的周期排列结构产生的物理特性，难以反映晶体学结构特性以及原子尺度的行为信息，因而，无法从根本上阐明微观组织演化过程中原子尺度上的动力学机理。

最近，ELDER等^[9-11]基于密度泛函理论提出了晶体相场(Phase-field-crystal，PFC)模型。该模型给出了新的能量函数形式，引入的序参量为局域密度场，它将液态的密度场定义为常量，将固相的密度场表示成周期性函数(波)的形式，进而通过周期性的原子密度函数表现晶体的晶格结构。这样的周期结构的原子密度场就能很自然地与弹性效应、晶粒取向和位错的运动等由周期结构产生的物理特性紧密地关联起来^[12]。PFC模型既可以描述晶体学结构特性以及原子尺度的行为，又可以揭示时间尺度为10^-6秒量级的原子、缺陷运动的行为特征。由此可以预见，PFC方法在今后的微结构演化的研究中将展现其强大的优势，为研究原子尺度组织结构的10^-6秒量级的行为特征，例如研究晶体内部的空位、位错的运动、晶界的迁移和微裂纹扩展过程及其对材料宏观性能的影响，提供先进和强有力的计算方法。

目前，PFC方法已经有了一些具体的应用，例如模拟位错滑移、攀移和湮没^[12-13]、结构转变^[14]、异质外延生长^[15]等。PFC方法最新的研究前沿和发展方向^[16-20]之一主要集中在：将加工变形的外界作用因素引入PFC模型中，建立形变和位错动力学的PFC模型，用于断裂、蠕变等行为和性能的机理研究。尽管ELDER等^[9]应用PFC方法在单轴拉伸条件下对裂纹扩展进行了初步模拟，但没有考虑热力学参数对裂纹的影响，特别是裂纹分叉和连通的微观细节没有反映出来，本文作者在文献[9]的基础上，采用双轴拉伸模型，结合PFC方法模拟纳米级微裂纹的扩展、分叉和连通的演化过程。

1  PFC模型

1.1  体系的能量函数

与传统的相场模型不同，PFC模型采用具有周期性的局域原子密度场变量作为相场变量^[9]。因此，PFC模型能够揭示晶体学结构特性以及原子尺度的行为。对于固态金属材料，其原子的位置不依赖于时间，呈规则排列。因此，要求相场变量必须能够反映原子周期性排列的特征。引入周期性相场变量，其局域位置的最大值对应于原子的位置；另一方面，均匀无序相(例如，液相、无序固溶体相)中的原子位置随时间随机变化，取时间平均可看成常量。符合这两方面要求的相场变量定义，可用原子密度场变量作为相场变量，其表达式可写成^[9]

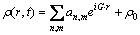                      (1)

式中：G为倒格矢，r为空间位置矢量，α _{n, m}为Fourier系数。式(1)中等号右边第一项反映晶格原子的周期排列结构特征；第二项ρ₀为反映均匀无序相的原子密度分布平均值，是一个常量。此时体系无量纲的能量函数F可以写成^[9]

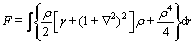              (2)

式中：γ为反映体系温度的参数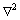，为Laplace算子。该能量函数自洽地包含了晶体结构的物理特征，例如多晶取向、弹性效应、塑性变形等。

1.2  二维体系的能量极小化

对于二维晶格点阵，倒格矢为G=nb₁+mb₂，其中b₁和b₂为倒格子基矢。对于三角格子，倒格子基矢可以写成

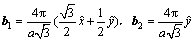              (3)

式中：a为晶格常数。

对二维体系的极小能量函数的二维解作单模近似，可得到平衡时三角格子固相的原子密度场变量ρ，其单模形式可写成^[9]

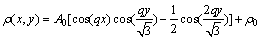    (4)

式中：A₀是一个特定常数，反映固相原子密度周期结构的振幅，由能量函数取极小值得到；q=2π/a。将式(4)代入式(2)，对A₀和q分别求导数，求出能量密度函数F₀，可写成

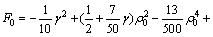
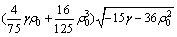            (5)

求得A₀的表达式为

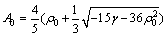                  (6)

式中：ρ₀和γ为体系能量函数的两个重要参数。由体系的能量密度函数可以计算并画出体系不同相区的相图。对于二维体系，相区有均匀无序相和固相，且固相有三角格子相和条状相两种。文献[9]已给出均匀相和条状相的能量密度函数表达式。按照平衡相图的计算方法得到的二维相图如图1所示。

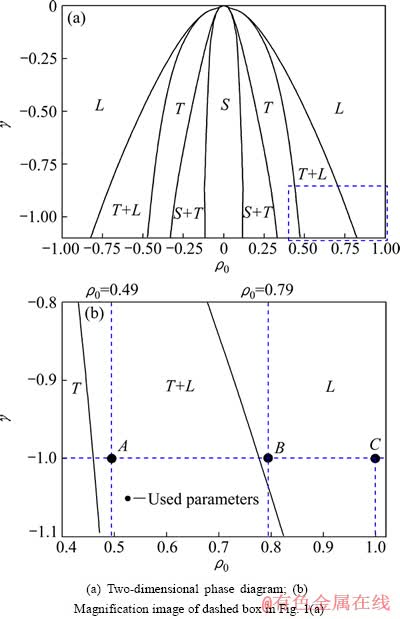
图1  PFC模型的二维相图^[9]

Fig. 1  Two-dimensional phase diagrams of PFC model^[9] (L, T and S represent liquid phase, triangular phase and stripe phase, respectively)

1.3  演化动力学方程与数值化处理

保守的原子密度场变量的演化可用与时间相关的Cahn-Hilliard动力学方程描述^{[9, 13]}

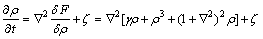    (7)

式中：ζ为Causs随机噪声项，具有零平均值。在本研究中不需考虑ζ的作用。

为求解动力学方程式(7)，还必须将动力学方程在时间和空间进行离散化处理, 即采用数值求解的办法。在本研究的数值求解中, 采用显式Euler迭代公式^[21-22]

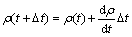                       (8)

式中：Δt为时间步长。此外，为使数值解具有稳定性，需将Laplace算子作用考虑到次近邻格点^[23]

     (9)

式中：Δx为空间步长，j和n分别代表i的最近邻格点与次近邻格点。

2  双轴拉伸应变模型

2.1  施加拉应变的方法

在受到拉伸作用后，样品中所有格点的坐标位置都会发生相应的变化。因此，通过格点的坐标位置变换来反映应变作用所引起的样品变形。设变形前的样品中格点位置的坐标用(x, y)表示，施加应变作用引起变形后，格点位置的坐标用(x′, y′)表示。样品在x方向和y方向分别受到应变ε_x和ε_y的拉伸作用，变形前后坐标变换关系为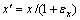和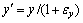。由于应变作用引起样品变形，其内部原子密度函数变为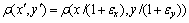，因此，在考虑应变作用引起变形的情况下，原子密度函数表达式(4)将变换为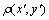，体系的能量也随之发生相应的变化，但控制演化的动力学方程的形式保持不变。

本研究模拟不涉及具体材料的物性参数，所用参数均已无量纲化处理^[9]，并将连续空间离散为四方格子网格, 采用周期性边界条件。计算区域网格为1 024×512 gp(gp表示格子点数)，空间步长设为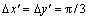，时间步长Δt=0.05，时间步用ts表示。

2.2  应变引起的原子间距变化

设模拟样品尺寸为1 024×512 gp，图2所示为从样品中截取500×500 gp的正方形区域的原子密度图。其中，图2(a)为没有加应变情况的截图，图2(b)为施加应变(ε_x=ε_y=10%)情况的截图。按照上节介绍的施加应变的方法，作用于完整的单晶样品。为了显示应变作用后原子间距离发生变化的细节，选取原子排列方向与x轴平行，以便观察原子密度分布的变化情况。

图2中AB和CD分别为变形前和变形后原子排列方向上原子位置的连线，其原子密度分布如图3(a)和(c)所示。图3(b)和(d)分别为图3(a)和(c)中方框区域的放大图。由于拉伸应变作用，图3(c)的原子间距变宽，原子间距约增加为10%。对比图3(a)和(c)可见，样品变形前的原子密度峰值有微小的周期波动(见图3(a))，周期约为100gp的距离。经10%的应变作用后，这种波动频率增加，周期变短，周期约为16gp的距离。

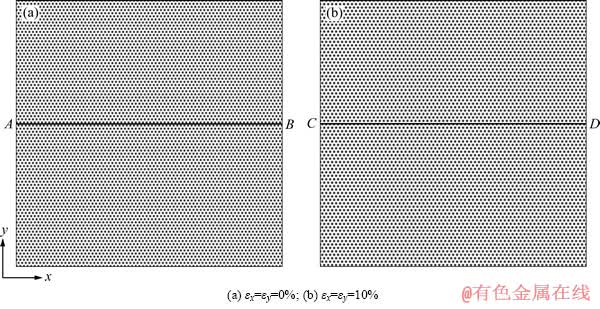
图2  原子排列方向与x轴平行的原子密度图

Fig. 2  Atomic density images with atomic arrangement direction paralleling to x axis

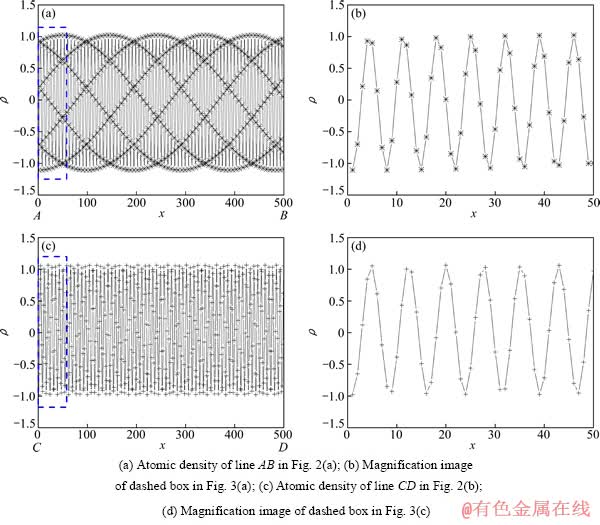
图3  原子密度随位置的变化曲线

Fig. 3  Curves of atomic density changes in relation to position

原子密度采用单模近似，能够近似地反映波动性。原子密度波动性与弹性应力波可发生耦合作用^[24]。对于沿y方向的原子排列原子密度分布也有类似的波动情况。

3  模拟结果与分析

3.1  初始裂口的设置

根据图1给出的相图，选取体系自由能密度函数的温度参数γ=-1.0，原子密度参数ρ₀=0.49(图1(b)中的A点)，位于均匀无序相与三角格子固相共存区。本研究对单晶样品进行模拟实验，其原子的排列方向与x轴夹角θ为15°。在样品的中心位置，挖出一个20×10 gp的长方形缺口作为初始裂口的位置，其局部放大图见图4。缺口处的参数设为γ=-1.0，ρ₀=0.79(图1(b)中的B点)，其正好处在均匀无序相与三角格子固相共存区附近的均匀相区。选取该点参数有利于三角晶相结构向裂纹结构转变。

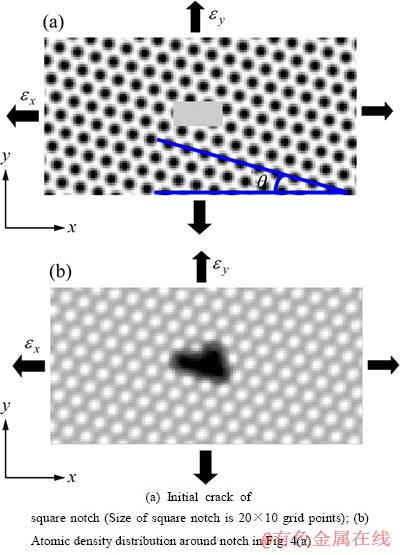
图4  初始裂口的局部放大图

Fig. 4  Magnification image of initial crack (ε_x and ε_y are stains along x and y axis, respectively)

3.2  裂纹的扩展分叉与连通

在制备的两个单晶样品中，温度参数值取γ=-1.0，原子密度参数ρ₀=0.49，沿x方向和y方向施加的应变分别为ε_x=7%和ε_y=10%。样品内各设置2个尺寸都为20×10 gp的长方形缺口，它们在同一条直线上排列，但相隔一段距离，观察裂纹的扩展连通过程，如图5所示。对于图5中a系列的裂纹，样品中两个初始缺口的原子密度都取ρ₀=0.79 (图1(b)中的B点)，尽管如此，初始裂口周围原子的环境仍会有微小差别。对于图5中b系列的裂纹，缺口的初始形状与a系列的缺口初始形状完全相同，唯一不同之处是b系列左边缺口处的ρ₀取0.79，而右边缺口处的ρ₀取1.0 (图1(b)中的C点)。

对比图5中的a系列和b系列的裂纹扩展演化图，可见a系列和b系列各自左边的缺口生成的裂纹演化图完全相同，表明各自右边的裂纹扩展没有对其产生明显的影响，但是各自右边缺口生成的裂纹，由于ρ₀值的不同，两者产生明显的差异。显而易见，b系列的右边缺口ρ₀=1.0的裂纹扩展较快，分叉也较多。由图6的体系能量随时间减少的速率可以看出，图5中b系列右边缺口的裂纹发展更快，产生的分叉也更多。这表明缺口处的原子密度ρ₀较大，有利于裂纹扩展分叉。由图5还可以看到，在裂纹周围出现灰白波纹分布，这是因为在裂纹扩展过程中裂纹周围的原子位移发生细微波动^[24]，这反映了裂纹周围畸变的场分布。

对比图5中a系列和b系列的两条主裂纹的交接，可以看出两者非常相似。由图5中的a和b系列还可见，子裂纹出现曲折的生长，边沿呈锯齿状，图7(a)给出了此处的局部放大图。由图7(a)可见，裂纹周围原子面成锯齿状，而不是平直的界面。子裂纹在扩展过程中，大多出现锯齿状结构，可以看成裂纹扩展过程的振荡现象，文献[25]也观察到类似现象。另外，图5(a5)的方框区域H中出现裂纹分叉，图7(b)给出了该区域的局部放大图。由该图可见，分叉处前方出现一串不连续的微小空洞。随着演化时间的增加，这些微小空洞将连成一线，成为新的分叉裂纹。在实际的裂纹扩展过程中，也常出现裂纹尖端发射位错或点缺陷的现象^[26-27]，这些缺陷发展成为微小空洞，再逐渐连接成条状和线状的裂纹。

3.3  应变大小的影响

设置初始长方形裂口位于样品的中心，在裂口处取ρ₀=1.0(图1(b)中的C点)，温度参数值取γ=-1.0。对样品的x方向和y方向同时施加应变。沿y方向的应变保持ε_y=10%，沿x方向的应变ε_x分别为3%、6%和9%，经过5.0×10⁵ ts演化的裂纹扩展分布如图8所示。图9所示为这3种不同应变下的能量变化曲线，由图9可见，裂纹在扩展过程中，能量在不断下降。当应变ε_x较小时(见图8(a))，裂纹不分叉，且关于中心对称，裂纹扩展的形状像一把“剑”，且存在锯齿边缘；对应的能量变化曲线近似成直线(见图9)。当应变ε_x=6%(见图8(b))，裂纹扩展过程中出现了较明显的分叉，裂纹形状转变成“虾”状；对应的能量下降速率加快。当应变ε_x=9%(见图8(c))，裂纹在扩展过程中出现一次分叉和二次分叉，裂纹形貌类似于“蟹”状，对应的能量下降曲线出现了明显向下弯曲(见图9)，表明体系能量加速减小，分叉越多，能量下降越快。

图5  同一条直线上的两个初始裂纹扩展过程

Fig. 5  Propagation process of two initial cracks on one line with ε_x=7% and ε_y=10%

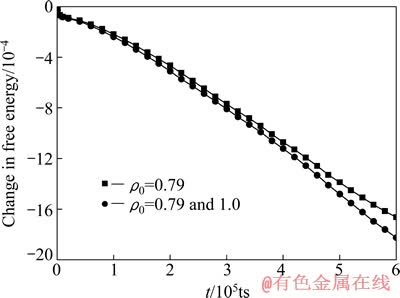
图6  体系具有直线平行排列的两个初始裂口的能量随时间变化曲线

Fig. 6  Changes in energy of system with two parallel initial cracks versus time

图7  图5(a5)中方框区域G和H的放大图

Fig. 7  Magnification images of rectangular region G (a) and H (b) in Fig. 5(a5)

图8  5.0×10⁵ ts时不同ε_x对应的裂纹扩展情况(ε_y=10%)

Fig. 8  Morphologies of crack propagation for 5.0×10⁵ ts at ε_y=10% and different ε_x

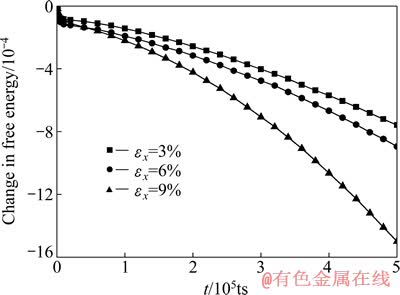
图9  不同ε_x情况下的能量随时间的变化曲线(ε_y=10%)

Fig. 9  Free energy change curves with time at ε_y=10% and different ε_x

4  结论

1) 采用双轴拉伸应变模型结合PFC方法，能够在原子空间尺度和扩散时间尺度较好地研究韧性材料的裂纹扩展和分叉的详细过程和细节，包括观察到裂纹直线扩展、分叉、二次分叉和连通。

2) 缺口处的均匀相原子密度较大，有利于微裂纹扩展分叉。在裂纹扩展过程中，体系能量在不断下降，表明应变能的释放比表面能的增加要快；当裂纹出现分叉时，体系能量减小得更快。微裂纹的子分枝出现锯齿折线结构，可看成裂纹扩展过程的振荡现象。在微裂纹扩展过程中，在分叉处前方出现若干微小的空洞，类似在裂纹尖端前方出现位错发射。

3) 对于直线排列的两条微裂纹，在扩展过程中，两裂尖靠近时，尖端相互吸引，引起裂纹相互连通。裂纹扩展的形状变化特征：应变较小时，裂纹形状像一把“剑”；随着应变增加，裂纹形状转变成“虾”状；最后，裂纹出现多个分支结构，裂纹形状变成了“蟹”状。

REFERENCES

[1] MOELANS N, BLANPAIN B, WOLLANTS P. An introduction to phase-field modeling of microstructure evolution[J]. Computer Coupling of Phase Diagrams and Thermochemistry, 2008, 32(2): 268-294.

[2] WANG Y, LI J. Phase field modeling of defects and deformation[J]. Acta Materialia, 2010, 58(4): 1212-1235.

[3] CHEN L Q. Phase-field models for microstructure evolution[J]. Annual Review of Materials Research, 2002, 32(1): 113-140.

[4] STEINBACH I. Phase-field models in materials science[J]. Modelling and Simulation in Materials Science and Engineering, 2009, 17: 73001-73008.

[5] 高英俊, 罗志荣, 胡项英, 黄创高. 相场方法模拟 AZ31 镁合金的静态再结晶过程[J]. 金属学报, 2010, 46(10): 1161-1172.

GAO Ying-jun, LUO Zhi-rong, HU Xiang-ying, HUANG Chuang-gao. Phase field simulation of static recrystallization for AZ31 Mg alloy[J]. Acta Metallurgica Sinica, 2010, 46(10): 1161-1172.

[6] 张宪刚, 宗亚平, 吴 艳. 相场再结晶储能释放模型与显微组织演变的模拟研究[J]. 物理学报, 2012, 61(8): 88104-88109.

ZHANG Xian-gang, ZONG Ya-ping, WU Yan. A model for releasing of stored energy and microstructure evolution during recrystallization by phase-field simulation[J]. Acta Physica Sinica, 2012, 61(8): 88104-88109.

[7] 龙永强, 刘 平, 刘 勇, 潘健生. 相场法模拟球形和盘形第二相粒子对晶粒长大的影响[J]. 中国有色金属学报, 2009, 19(1): 84-89.

LONG Yong-qiang, LIU Ping, LIU Yong, PAN Jian-sheng. Phase field modeling for effects of spherical and discal second-phase particles on grain growth[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(1): 84-89.

[8] MILLETT P C, SELVAM R P, SAXENA A. Molecular dynamics simulations of grain size stabilization in nanocrystalline materials by addition of dopants[J]. Acta materialia, 2006, 54(2): 297-303.

[9] ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Physical Review E, 2004, 70(5): 051605-051618.

[10] ELDER K R, KATAKOWSKI M, HAATAJA M, GRANT M. Modeling elasticity in crystal growth[J]. Physical Review Letters, 2002, 88(24): 245701-245704.

[11] BERRY J, GRANT M, ELDER K R. Diffusive atomistic dynamics of edge dislocations in two dimensions[J]. Physical Review E, 2006, 73(3): 31609-31615.

[12] 任 秀, 王锦程, 杨玉娟, 杨根仓. 纯物质晶界结构及运动的晶体相场法模拟[J]. 物理学报, 2010, 59(5): 3595-3600.

REN Xiu, WANG Jin-cheng, YANG Yu-juan, YANG Gen-cang. Simulation of the structure and motion of grain boundary in pure substances by phase field crystal model[J]. Acta Physica Sinica, 2010, 59(5): 3595-3600.

[13] 杨 涛, 陈 铮, 董卫平. 应力诱发双位错组亚晶界湮没的晶体相场模拟[J]. 金属学报, 2011, 47(10): 1301-1306.

YANG Tao, CHEN Zhen,DONG Wei-ping. Phase field crystal simulation of stress induced annihilation of sub-grain boundary with double-array dislocation[J]. Acta Metall Sinica, 2011, 47(10): 1301-1306.

[14] 高英俊, 罗志荣, 黄创高, 卢强华, 林 葵. 晶体相场方法研究二维六角相向正方相结构转变[J]. 物理学报, 2013, 62(5): 050507-0505010.

GAO Ying-jun, LUO Zhi-rong, HUANG Chuang-gao, LU Qiang-hua, LIN Kui. Phase field crystal modeling for 2D transformation from hexagonal to square structure[J]. Acta Physica Sinica, 2013, 62(5): 050507-0505010.

[15] YU Y M, BACKOFEN R, VOIGT A. Morphological instability of heteroepitaxial growth on vicinal substrates: A phase-field crystal study[J]. Journal of Crystal Growth, 2011, 318(1): 18-22.

[16] STEFANOVIC P, HAATAJA M, PROVATAS N. Phase field crystal study of deformation and plasticity in nanocrystalline materials[J]. Physical Review E, 2009, 80(4): 046107-046114.

[17] CHAN P Y, TSEKENIS G, DANTZIG J, DAHMEN K A, GOLDENFELD N. Plasticity and dislocation dynamics in a phase field crystal model[J]. Physical Review Letters, 2010, 105: 15502-15508.

[18] HUANG Z F, ELDER K R, PROVATAS N. Phase-field-crystal dynamics for binary systems: Derivation from dynamical density functional theory, amplitude equation formalism, and applications to alloy heterostructures[J]. Physical Review E, 2010, 82(2): 21605-21615.

[19] HUANG S, ZHANG S, BELYTSCHKO T, TERDALKAR S, ZHU T. Mechanics of nanocrack: Fracture, dislocation emission, and amorphization[J]. Journal of the Mechanics and Physics of Solids, 2009, 57(5): 840-850.

[20] JATINEN A, NISSILA T. Eighth-order phase-field-crystal model for two-dimensional crystallization[J]. Physical Review E, 2010, 82(6): 061602-061607.

[21] CHEN L Q, YANG W. Computer simulation of the domain dynamics of a quenched system with a large number of nonconserved order parameters: The grain-growth kinetics[J]. Physical Review B, 1994, 50(21): 15752-15756.

[22] 高英俊, 罗志荣, 张少义, 黄创高. 相场方法研究Al-Ag合金γ相周围溶质析出过程[J]. 金属学报, 2010, 46(12): 1473-1480.

GAO Ying-jun, LUO Zhi-rong, ZHANG Shao-yi, HUANG Chuang-gao. Phase-field simulation of solute precipitations around the γ phase in Al-Ag alloy[J]. Acta Metallurgica Sinica, 2010, 46(12): 1473-1480.

[23] OONO Y, PURI S. Computationally efficient modeling of ordering of quenched phases[J]. Physical Review Letters, 1987, 58(8): 836-839.

[24] CRAWFORD C, RIECKE H. Oscillon-type structures and their interaction in a Swift-Hohenberg model[J]. Physica D: Nonlinear Phenomena, 1999, 129(1): 83-92.

[25] SHARON E, FINEBERG J. Confirming the continuum theory of dynamic brittle fracture for fast cracks[J]. Nature, 1999, 397(6717): 333-335.

[26] ZHU T, LI J, YIP S. Atomistic study of dislocation loop emission from a crack tip[J]. Physical Review Letters, 2004, 93(2): 025503-025507.

[27] BUEHLER M J, ABRAHAM F F, GAO H J. Hyperelasticity governs dynamic fracture at a critical length scale[J]. Nature, 2003, 426(6963): 141-146.

(编辑  何学锋)

基金项目：国家自然科学基金资助项目(51161003, 50661001)；广西省自然科学基金重点资助项目(2012GXNSFDA053001)；广西大学广西有色金属及特色材料加工重点实验室开放基金资助项目(GXKFJ12-01)；广西大学科研基金资助项目(XJZ110611)

收稿日期：2012-09-22；修订日期：2013-04-20

通信作者：高英俊，教授，博士；电话：0771-3239478；E-mail：gaoyj@gxu.edu.cn