降级路网组合出行交通流分配模型与算法
孟梦1, 2,邵春福1,曾靖静1,董春娇3,诸葛承祥1
(1. 北京交通大学 城市交通复杂系统理论与技术教育部重点实验室,北京,100044;
2. 南洋理工大学 土木与环境工程学院,基建系统中心,新加坡,639798;
3. 田纳西大学 交通研究中心,美国田纳西,37996)
摘要:研究降级路网条件下的组合出行交通平衡问题。首先,基于出行者对降级路网的不同风险态度,将出行者分为3类:守时型、冒险型和平均型。其次,考虑小汽车出行和小汽车换乘地铁出行2种出行模式,分析降级路网条件下不同用户类的组合出行行为,建立相应的多用户变分不等式交通分配模型,讨论模型解的性质。最后,设计模型的求解算法,并通过算例说明模型和算法的有效性。结果表明:不同出行时间预算的出行者在降级路网中的路径选择行为存在较大差异,路网降级程度对出行者出行选择行为影响显著;随着道路通行能力的降低,出行者更倾向于选择组合出行模式。
关键词:降级路网;组合出行模式;变分不等式
中图分类号:U491.1 文献标志码:A 文章编号:1672-7207(2014)02-0643-07
Traffic assignment model and algorithm with combined modes in a degradable transportation network
MENG Meng1, 2, SHAO Chunfu1, ZENG Jingjing1, DONG Chunjiao3, ZHUGE Chengxiang1
(1. Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Ministry of Education,
Beijing Jiaotong University, Beijing 100044, China;
2. Centre for Infrastructure Systems, School of Civil and Environmental Engineering,
Nanyang Technological University, Singapore 639798, Singapore;
3. Center for Transportation Research, The University of Tennessee, TN37996, USA)
Abstract: To study the effect of the degradable road network on travel decision and traffic assignment, firstly all travelers were categorized into three classes: risk-averse travelers, risk-prone travelers and risk-neutral travelers. Secondly, two travel modes including car trip and car-subway trip were considered in a multi-modal networks. A stochastic traffic equilibrium model was proposed by using the variational inequality theory, and the properties of the solution were discussed. Finally, an example was used to testify the validity of the model and the algorithm. The results show that the travel behavior varies greatly with different travel time budget; with the decrease of traffic capacity, travelers prefer to choose the combined modes.
Key words: degradable transportation network; combined modes; variational inequality
随着大城市综合交通系统的日益完善,组合出行模式逐渐成为居民日常出行的主要形式。在组合出行模式下,出行者不仅选择出行路径,还要选择交通方式。与单一方式出行相比,组合出行研究更能真实地反映出行者的交通选择行为与交通运行状态,是近年来专家学者的研究热点[1-5]。然而,以往组合出行分配模型均假定道路通行能力是固定不变的。在现实交通网络中,由于多种不确定性因素的存在(如天气、交通事故、交通管制等),容易造成路网整体或局部通行能力不同程度的降级,导致出行者对出行时间的理解发生变化,从而影响出行者的出行决策[6-9]。现有降级路网的研究中,Du等[10]分析了降级路网中的出行者路径选择行为,构建了降级路网交通流分析方法的一般框架;黎茂盛等[11]分析了出行者对降级路网的认知过程,并建立了降级路网中的交通平衡模型。近年来,Lo等[12]提出了出行时间预算的概念,认为不同出行者对待路网降级时会有不同的风险态度,会不同幅度地增加出行时间预算以避免出行延误,进而将降级路网的研究深入到多用户出行的情况。何胜学[13]将Lo的数学规划模型转化为更通用的变分不等式形式,避免了对非线性非凸约束集进行处理。要甲等[14]将基于出行时间预算的交通分配模型扩展到由城市道路网络和地铁网络组成的多方式交通网络,但没有考虑交通方式间的换乘情况,不能实际地反映现实中组合出行行为。多方式交通网络中,由于城市道路网存在多种不确定因素,造成道路通行能力不同程度的降级,因此出行者的出行时间会发生随机变化。而地铁行驶在固定的线路上,运行时间不受外界影响,出行者的出行时间相对固定。本文作者综合考虑降级路网中的组合出行分配问题,假定每个OD对(Origin-destination pair) 之间存在2种常见的出行模式,小汽车出行和小汽车换乘地铁出行。根据出行者对降级路网的不同态度,将出行者分为3类:保守型、冒险型和平均型。基于超级网络理论和扩展技术,构造多方式交通超级网络,分析降级路网条件下不同出行者的组合出行行为,建立与随机平衡等价的变分不等式交通分配模型,并借助连续权重平均法(method of successive weight average, MSWA)算法求解模型,通过算例验证了模型和算法的有效性。
1 符号定义及超级网络
传统的交通网络是由许多节点和连接2个节点之间的边组成的[15-16],一般来说,节点代表道路交叉口和公交站点等,连接的边代表路段,公交线路等,这些边具有通行时间、通行费用和通行能力等多种属性。随着交通网络规模的不断扩大和结构的日益复杂,传统的单模式交通网络难以充分地描述组合出行模式下的交通网络特征,例如不同交通方式有各自独立的拓扑结构,各种交通方式子网络之间通过换乘行为相互关联,换乘时会存在换成费用、换乘时间及等待时间等多种属性。针对上述问题,可以引入“超级网络”[17]的概念,考虑组合出行模式的交通网络可以由一个包含多种交通方式子网的超级网络来表示。该超级网络是在普通网络的基础上,将不同的交通方式划分为不同独立的子网络层,子网络间通过添加虚拟弧段来表达换乘关系。
考虑交通网络G=(N,L),N为节点集合,L为路段集合,l为其中的一条路段,l∈L;A,B分别表示城市道路路段集合和地铁路段集合,E为换乘路段集合,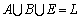 ;M为交通方式集合,a,b分别表示小汽车和地铁,a,b∈M,后文中含有“a”,“b”上下标的变量分别表示对应的子网络;I网络中出行者类型的集合,i为其中的一个类型;W为网络中的OD对集合,w为其中的一个OD对;
;M为交通方式集合,a,b分别表示小汽车和地铁,a,b∈M,后文中含有“a”,“b”上下标的变量分别表示对应的子网络;I网络中出行者类型的集合,i为其中的一个类型;W为网络中的OD对集合,w为其中的一个OD对;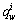 为OD对w间用户类i的交通需求;Kw为OD对w间所有路径的集合,k为其中的一条路径,
为OD对w间用户类i的交通需求;Kw为OD对w间所有路径的集合,k为其中的一条路径,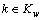 ;fk为路径k上的流量,xl为路段l上的流量;
;fk为路径k上的流量,xl为路段l上的流量;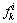 为路径k上用户类i的流量,
为路径k上用户类i的流量,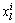 为路段l上用户类i的流量,且满足
为路段l上用户类i的流量,且满足 。
。
基于超级网络理论和扩展技术,将图1所示的普通路网转化为图2所示的超级交通网络。图2中实线表示行驶路段,虚线表示换乘路段,点线表示上下网路段。路段上的权值可以代表行驶时间、出行费用、舒适度等多种属性,从而出行者可以通过一条超级路径实现普通网络上不同方式和线路间的换乘行为。
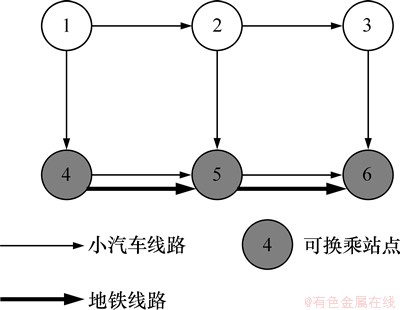
图1 多方式交通网络
Fig. 1 Multi-modal transportation network
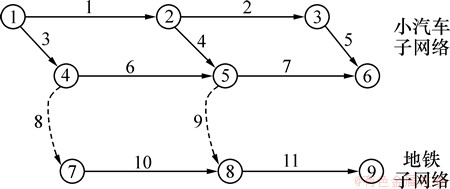
图2 超级网络
Fig. 2 Super network
2 出行时间预算
2.1 期望出行时间
降级路网条件下,城市道路的路段通行能力衰减而发生随机扰动,因而城市道路的路段出行时间是一个随机变量[12]。而地铁网络是一个相对确定的系统,路段出行时间可以看作由地铁运行时间得到的定值。组合出行模式中,出行时间不仅包括各交通方式子网络上的运行时间,还要考虑换乘时间。假设路段出行时间相互独立,因此,路径出行时间可以表示为
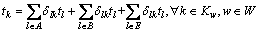 (1)
(1)
式中:tk为OD对w之间路径k的出行时间;tl为路段l的出行时间;δlk为路段与路径的关联关系,若路段l在路径k上,则δlk为1,否则为0。
本文采用BPR函数(bureau of public roads function)计算城市道路网中的路段出行时间,即
 (2)
(2)
式中: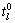 和xl分别为路段l上的自由流行驶时间和流量;Cl为路段l的通行能力;ξ为小汽车平均载客人数。传统的交通分配模型中,城市道路的通行能力固定不变,然而,考虑到外界因素的干扰,路段通行能力是一个随机变量,路段出行时间无法预先获得,使得路段出行时间会形成某种概率分布。假定该随机变量Cl服从
和xl分别为路段l上的自由流行驶时间和流量;Cl为路段l的通行能力;ξ为小汽车平均载客人数。传统的交通分配模型中,城市道路的通行能力固定不变,然而,考虑到外界因素的干扰,路段通行能力是一个随机变量,路段出行时间无法预先获得,使得路段出行时间会形成某种概率分布。假定该随机变量Cl服从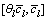 上的均匀分布[12-14],
上的均匀分布[12-14],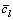 为路段l的设计通行能力,
为路段l的设计通行能力,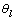 为路段l通行能力的最大降级系数。因此,城市道路的路段出行时间tl也是一个随机变量,其均值E(tl)和方差
为路段l通行能力的最大降级系数。因此,城市道路的路段出行时间tl也是一个随机变量,其均值E(tl)和方差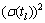 分别为
分别为
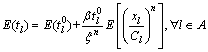 (3)
(3)
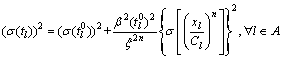 (4)
(4)
假设路段自由流出行时间是一个固定常数,且路段流量与随机干扰相互独立,因此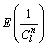 和
和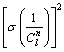 可表示为
可表示为
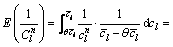
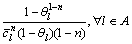 (5)
(5)

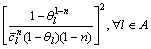 (6)
(6)
整理化简后,城市道路的路段出行时间的均值和方差式可表示为
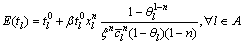 (7)
(7)
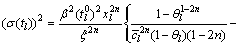
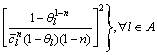 (8)
(8)
假定地铁网络中的路段出行时间仅由地铁运行时间决定,而换乘路段的出行时间包括步行时间和等待时间,即
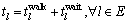 (9)
(9)
式中: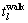 为路段l上的步行时间;
为路段l上的步行时间;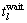 为路段l上的等待时间,
为路段l上的等待时间,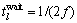 (f为目的换乘线路的发车频率,单位是辆/h)。
(f为目的换乘线路的发车频率,单位是辆/h)。
由中心极限定理,出行者的路径出行时间tk服从正态分布,其均值E(tk)和方差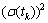 分别为
分别为
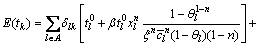
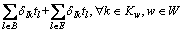 (10)
(10)
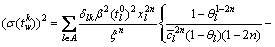
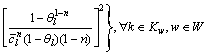 (11)
(11)
2.2 出行时间预算
城市道路网路段通行能力的降级导致路段及路径出行时间发生随机变化,因此出行者不能准确预测其出行时间。面对交通网络的不确定性,为准点到达目的地,不同的出行者会不同程度增加出行时间预算,即提早出行。Siu等[7]提出出行时间预算(travel time budget, TTB)的概念,认为出行者会选择出行时间预算最小的路径出行,出行时间预算等于期望出行时间与增加的出行时间之和,即
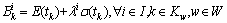 (12)
(12)
式中: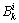 为类型i的出行者对路径k的出行时间预算;
为类型i的出行者对路径k的出行时间预算;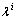 为校正参数,表示出行者对出行时间可靠性的要求程度;
为校正参数,表示出行者对出行时间可靠性的要求程度;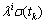 为类型i的出行者增加的出行时间预算。
为类型i的出行者增加的出行时间预算。
根据出行者对出行时间可靠性的要求不同,可以将出行者分为3类:守时型、冒险型和平均型。守时型出行者,对应较大的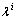 ,对出行时间可靠性的要求较高,为确保能准点到达目的地,宁愿增加额外的出行预算(提早出门),以避免由于路段出行时间发生大幅度变化而延误到达时间。冒险型出行者,对应较小的
,对出行时间可靠性的要求较高,为确保能准点到达目的地,宁愿增加额外的出行预算(提早出门),以避免由于路段出行时间发生大幅度变化而延误到达时间。冒险型出行者,对应较小的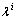 (如负数),具有冒险心理,倾向于选择预期出行时间较短的路径,即便可能遭受损失也是如此。平均型出行者,
(如负数),具有冒险心理,倾向于选择预期出行时间较短的路径,即便可能遭受损失也是如此。平均型出行者,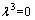 ,介于两类出行者之间,不考虑出行时间的变动,选择期望出行时间最短的路径出行。
,介于两类出行者之间,不考虑出行时间的变动,选择期望出行时间最短的路径出行。
假定每类出行者都选择出行时间预算最短的路径出行,在经过一段时间的学习和调整后,交通网络会达到一个平衡的状态[14]。平衡状态下,对每一类出行者,每一个OD对之间的被使用的路径的出行时间预算最小且相等,而且不大于未被使用的路径的出行时间预算,即
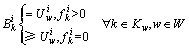 (13)
(13)
式中: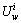 为OD对w之间用户类i的最小出行时间预算。
为OD对w之间用户类i的最小出行时间预算。
3 模型建立
网络平衡条件(13)可以构建如下的变分不等式 模型。
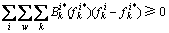 (14)
(14)
式中:上标*表示该变量在平衡态下的取值。可行域由以下约束条件组成:
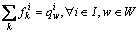 (15)
(15)
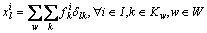 (16)
(16)
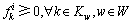 (17)
(17)
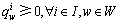 (18)
(18)
定理1 变分不等式模型式(14)等价于组合出行模式下多方式交通网络平衡条件式(13)。
证明:首先,由式(13)可以得到:
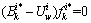 (19)
(19)
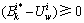 (20)
(20)
结合式(17)得:
 (21)
(21)
对所有OD对及用户类型求和:
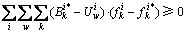 (22)
(22)
展开后,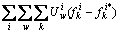 为0,故可以得到式(14)。
为0,故可以得到式(14)。
由于式(14)等价于式(22),因此利用式 (22)推证式(13)成立。在式(22)中,令所有非路径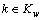 且非用户类i的路径流量均等于平衡状态下的路径流量,式(22)可以化简为:
且非用户类i的路径流量均等于平衡状态下的路径流量,式(22)可以化简为:
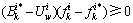 (23)
(23)
当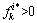 时,
时,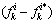 可正可负,因此要推得式(23)成立,
可正可负,因此要推得式(23)成立,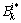 必须等于
必须等于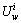 。而当
。而当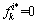 时,由于
时,由于 ,要推得式(23)成立,
,要推得式(23)成立,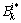 必须大于或等于
必须大于或等于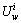 。对所有路径及用户类型进行上述推导,可以得到式(13)成立。综上可得,式(13)等价于式(14)。证毕。
。对所有路径及用户类型进行上述推导,可以得到式(13)成立。综上可得,式(13)等价于式(14)。证毕。
定理2 变分不等式模型式(14)至少存在一个解。
证明:将变分不等式模型式(14)整理成矩阵的形式表示如下:
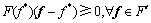 (24)
(24)
式中,f为由所有用户类型-路径流量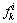 所组成的列向量;F′为对应式(16)中的可行路径流向量的有界闭凸集。同时函数F(f)连续,根据Brouwer不动点定理,模型至少存在一个解。若进一步假定路段出行时间是路段流量的严格单调递增函数,则该模型具有唯一解。
所组成的列向量;F′为对应式(16)中的可行路径流向量的有界闭凸集。同时函数F(f)连续,根据Brouwer不动点定理,模型至少存在一个解。若进一步假定路段出行时间是路段流量的严格单调递增函数,则该模型具有唯一解。
4 求解算法
网络平衡条件(13)可以构建如下的变分不等式模型。本文设计一个基于连续权重平均法(method of successive weight average, MSWA)[18]的算法来求解变分不等式模型。该方法与传统的迭代加权法(method of successive average, MSA)的不同之处在于迭代步长不是一个固定值,而是随着迭代点接近最优解,将更多的权重分配给后迭代点,求解的收敛速度可以得到明显的提升。
Step 1: 初始化。置迭代次数n=1,令各路段流量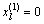 ,在自由流路段出行时间{tl(0)}的基础上,计算路径出行时间预算
,在自由流路段出行时间{tl(0)}的基础上,计算路径出行时间预算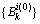 ;将每个用户类的出行需求
;将每个用户类的出行需求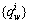 在路网上进行全无分配,得到初始可行路段流量
在路网上进行全无分配,得到初始可行路段流量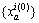 ;
;
Step 2: 路段出行时间预算更新。令
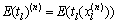 ,
,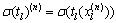 ;
;
Step 3: 确定下降方向。基于当前的出行时间期望及标准差,计算出行时间预算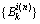 ,将
,将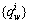 在路网上进行全有全无分配,得到辅助路段流量
在路网上进行全有全无分配,得到辅助路段流量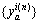 ;
;
Step 4: 移动。使用MSWA更新每一个用户类的路段流量,其中d取1,即
 (25)
(25)
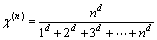 (26)
(26)
Step 5: 收敛判断。若收敛性满足预定要求,停止迭代,输出解,否则令n=n+1,返回Step 2。本文采用如下收敛准则,其中ε是预先给定的误差限值。
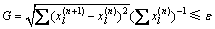 (27)
(27)
5 算例分析
采用如图1和图2所示的算例网络,有1个OD对 (1,6),路网中有3类出行者,记为类型1,类型2和类型3,对应参数分别为λ1=2,λ2=-1,λ3=0,每类出行者各有5 000人。路段10和11为一条地铁线路的一部分,与城市道路路段6和7对应。小汽车网络各弧段参数见表1。地铁路段运行时间分别为: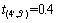 h,
h,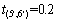 h。换乘路段:
h。换乘路段: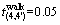 h,
h,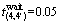 h,
h, ,
,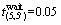 h。其他参数:ξ= 1 人/辆;β=0.15,n=4,ε=0.001。
h。其他参数:ξ= 1 人/辆;β=0.15,n=4,ε=0.001。
表1 小汽车子网络路段参数
Table 1 Parameters of car sub network

图3给出了算法的收敛性能。从图3可以看出:MSWA算法经过305次迭代可达到预定收敛精度的要求。而相同条件下,MSA算法需要迭代609次才可达到相同精度。虽然MSA算法在迭代初期下降较快,但由于步长设置的限制,在接近最优解时收敛速度缓慢;因此,MSWA算法较MSA算法在迭代速度和收敛精度上都更有优势,可以有效地求解本文模型。
表2给出了不同路网条件下的平衡分配结果,包括常规路网、轻微降级路网(路段降级系数为0.85)、中度降级路网(路段降级系数为0.7)、及重度降级路网(路段降级系数为0.55)。表2中出行模式Car和P&R分别代表为小汽车出行模式和小汽车换乘地铁出行模式。
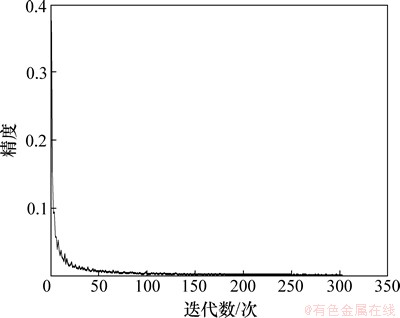
图3 算法收敛性
Fig. 3 Convergence of algorithm
表2 不同路网条件下的流量分配结果
Table 2 Equilibrium results under different road conditions
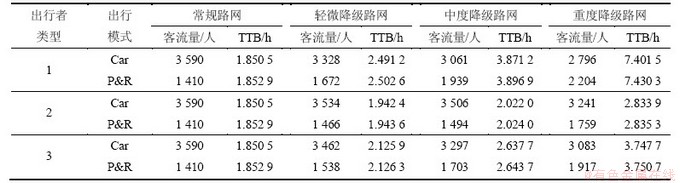
算例结果分析可知,随着道路通行能力降级的加剧,选择小汽车出行的交通量减少,选择组合出行的交通量增加。这是因为道路通行能力降级的加剧导致道路出行时间变大,而地铁运行时间固定,保证了出行时间的可靠性。道路通行能力降级程度越大,出行者越倾向于选择组合出行模式出行。
随着路网降级程度的加剧,不同类型出行者增加的出行时间预算明显不同。如图4所示,相同的降级幅度后,3类出行者增加的出行时间预算均有所增加,但增加幅度不同,守时型出行者增加幅度最大,冒险型出行者增加幅度最小,平均型出行者增加幅度介于守时型和冒险型之间。
随着道路通行能力的降低,出行者出行预算的增加,不同类型出行者选择小汽车出行的比例不同程度的减少,减幅大小依次是守时型、平均型、冒险型,如图5所示。这是因为:守时型出行者对到达时间可靠性要求高,在道路通行能力降低时,及时增加出行预算,调整出行模式。冒险型出行者不愿意增加出行时间预算,即使出行时间可变,认为仍有机会按预期到达目的地。平均型出行者在路网降级过程中对出行时间的变化不太敏感,其路径出行时间预算等于路径出行时间的均值。
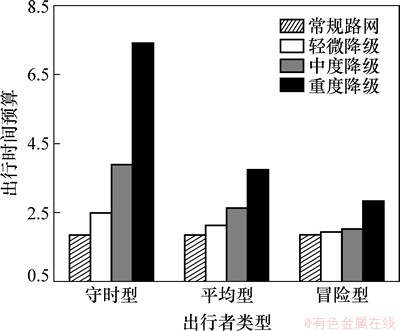
图4 不同路网条件下各类型出行者的出行时间预算
Fig. 4 Time budget under different road conditions
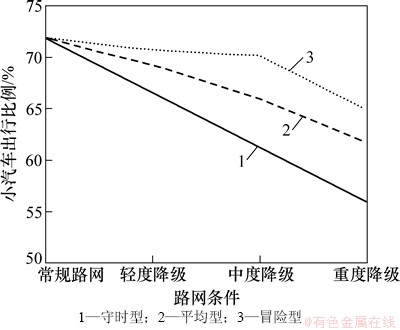
图5 不同路网条件下各类型出行者选择小汽车出行的比例
Fig. 5 Car trip proportions under different road conditions
6 结论
(1) 出行者对待路网降级的风险认知程度会对其出行选择具有显著的影响。不同的交通情况,会不同类型的出行者影响也有所不同。
(2) 道路通行能力的降低,出行者出行预算增加,不同类型出行者出行预算增加幅度不同。
(3) 出行者出行预算增加,选择小汽车出行的比例不同程度的减少,使得组合出行模式更占有优势。
(4) 把出行时间的不确定性引入组合出行交通分配模型,更能反映实际出行行为,为制定有效地管理措施提供更准确的决策支持。
参考文献:
[1] Wu Z X, Lam W H K. Network equilibrium for congested multi-mode networks with elastic demand[J]. Journal of Advanced Transportation, 2003, 37(3): 295-318.
[2] Lo H K, Yip C W, Wan K H. Modeling transfer and non-linear fare structure in multi-modal network[J]. Transportation Research Part B, 2003, 37(2): 149-170.
[3] Garía R, Marín A. Network equilibrium with combined modes: Models and solution algorithms[J]. Transportation Research Part B, 2005, 39(3): 223-254.
[4] 孟梦, 邵春福, 曾靖静, 等. 停车换乘下组合出行模型与算法[J]. 吉林大学学报(工学版), 2013, 43(6): 1465-1470.
MENG Meng, SHAO Chunfu, ZENG Jingjing, et al. Model and algorithm of combined trip under park and ride[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(6): 1465-1470.
[5] 孟梦, 邵春福, 曾静靖, 等. 组合出行模式下多方式交通流分配模型及算法[J]. 吉林大学学报(工学版), 2014, 44(1): 47-53.
MENG Meng, SHAO Chunfu, ZENG Jingjing, et al. A multi-modal traffic equilibrium model and algorithm with combined mode[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(1): 47-53.
[6] Lam W H K, Shao H, Sumalee A. Modeling impacts of adverse weather conditions on a road network with uncertainties in demand and supply[J]. Transportation Research Part B, 2008, 42(10): 890-910.
[7] Siu B W Y, Lo H K. Doubly uncertain transportation network: degradable capacity and stochastic demand[J]. European Journal of Operational Research, 2008, 191(1): 166-181.
[8] Meng M, Shao C F, Zeng J J, et al. Stochastic user equilibrium with combined mode in a degradable multi-modal transportation network[J] Journal of Computers, 2012, 7(12): 3005-3012.
[9] 张小宁, 李乐园, 张红军. 通行能力变化时的瓶颈交通分配模型应用研究[J]. 同济大学学报(自然科学版), 2008, 36(3): 315-318.
ZHANG Xiaoning, LI Leyuan, ZHANG Hongjun. Application of dynamic traffic assignment model with time-varying bottleneck capacity[J]. Journal of Tongji University (Natural Science), 2008, 36(3): 315-318.
[10] Du Z P, Nicholson A. Degradable transportation systems: sensitivity and reliability analysis[J]. Transportation Research Part B, 1997, 31(3): 225-237.
[11] 黎茂盛, 王炜, 史峰. 退化道路网的认知与交通流均衡分析模型[J]. 中国公路学报, 2006. 19(6): 87-91.
LI Maosheng, WANG Wei, SHI Feng. Cognition of degraded road network and equilibrium analysis model on traffic flow[J]. China Journal of Highway and Transport, 2006, 19(6): 87-91.
[12] Lo H K, Luo X W, Siu B W Y. Degradable transport network: travel time budget of travelers with heterogeneous risk aversion[J]. Transportation Research Part B, 2006, 40(9): 792-806.
[13] 何胜学. 基于出行时间预算的多用户交通分配模型及算法[J]. 公路交通科技, 2009, 26(5): 107-111, 116.
HE Shengxue. Multi-class traffic assignment model and algorithm based on travel time budget[J]. Journal of Highway and Transportation Research and Development, 2009, 26(5): 107-111, 116.
[14] 要甲, 史峰, 周钊, 等. 基于出行时间预算的多模式多类用户城市交通均衡分析[J]. 中南大学学报(自然科学版), 2011, 42(11): 3572-3577.
YAO Jia, SHI Feng, ZHOU Zhao, et al. Multi-mode and multi-class user’s urban transportation equilibrium[J]. Journal of Central South University (Science and Technology), 2011, 42(11): 3572-3577.
[15] LIU Lihua, CHEN Jianer, CHEN Qongqiao, et al. An new representation for interconnection network structures[J]. Journal of Central South University of Technology, 2002, 9(1): 47-53.
[16] 曾明华, 李夏苗. 基于层次性的交通网络资源优化配置方法[J]. 中南大学学报(自然科学版), 2011, 42(1): 247-253.
ZENG Minghua, LI Xiamiao. Optimal allocation approach of transport network resource based on hierarchical property[J]. Journal of Central South University (Science and Technology), 2011, 42(1): 247-253.
[17] Nagurney A, Dong J. Supernetworks: Decision-making for the information age[M]. Cheotenham: Edward Elgar Publishers, 2002: 10-15.
[18] Liu H X, He X Z, He B S. Method of successive weighted averages(MSWA) and self-regulated averaging schemes for solving stochastic user equilibrium problem[J]. Networks & Spatial Economics, 2009, 9(4): 485-503.
(编辑 赵俊)
收稿日期:2013-01-24;修回日期:2013-04-30
基金项目:国家重点基础研究发展计划(“973”计划)项目(2012CB725403);国家自然科学基金国际重大合作项目(71210001);中央高校基本科研业务费专项资金资助项目(2013YJS047)
通信作者:邵春福(1957-),男,河北沧州人,教授,博士生导师,从事交通规划、智能交通系统及交通安全研究;电话:010-51682236;E-mail:cfshao@bjtu.edu.cn