网络首发时间: 2018-03-12 09:35

稀有金属 2019,43(06),613-620 DOI:10.13373/j.cnki.cjrm.xy18020002

ATI 718Plus镍基高温合金机制型本构模型研究

史晓楠 刘莹莹 宁永权 张君彦 王梦婷

西安建筑科技大学冶金工程学院

西北工业大学材料学院

摘 要：

采用Gleeble-1500D热模拟试验机进行等温压缩实验, 研究了ATI 718Plus镍基高温合金在变形温度980～1140℃, 应变速率0.001～1.000 s^-1条件下的高温流变行为。结果表明:ATI 718Plus高温合金的流变应力随应变速率的降低或变形温度的升高显著降低, 其热变形激活能为517.5 kJ·mol^-1。同时, 该合金的应力应变曲线具有明显的动态再结晶 (DRX) 特征, 变形量、变形温度以及应变速率对动态再结晶体积分数均具有显著影响。此外, 以η-Ni₃Al_0.5Nb_0.5相溶解温度为临界条件构建了718Plus高温合金3个变形阶段的本构模型:以弹性模量为内变量建立了弹性变形阶段的本构模型, 基于位错密度演化构建了加工硬化-动态回复阶段本构模型, 以再结晶动力学为基础建立了动态再结晶阶段本构模型。建立的本构模型精度较高, 相关系数R=0.998, 平均相对误差AARE=2.26%, 能够较为精确地表征合金的高温变形行为。

关键词：

ATI 718Plus高温合金;本构模型;热变形激活能;动态回复;动态再结晶;

中图分类号： TG132.3

作者简介：史晓楠 (1990-) , 男, 河南安阳人, 硕士研究生, 研究方向:高温合金塑性加工工艺, E-mail:xiaonan5792@163.com;*刘莹莹, 副教授;电话:029-82205097;E-mail:wfllyy7779@163.com;

收稿日期：2018-02-01

基金：国家自然科学基金项目 (51775440);陕西省国际合作与交流项目 (2016KW-054) 资助;

Physically-Based Constitutive Model of Nickel-Based Superalloy ATI 718Plus

Shi Xiaonan Liu Yingying Ning Yongquan Zhang Junyan Wang Mengting

School of Metallurgical Engineering, Xi'an University of Architecture and Technology

School of Materials Science and Engineering, Northwestern Polytechnical University

Abstract：

The high-temperature deformation behaviour of ATI 718 Plus superalloy was investigated by a series of isothermal compression tests at temperatures of 980～1140℃ and strain rates of 0.001～1.000 s^-1 on the Gleeble-1500 D simulator. The results showed that the flow stress decreased significantly with dropped strain rate or elevated deformation temperature. The hot deformation activation energy of ATI 718 Plus was calculated as 517.5 kJ·mol^-1. The true stress-strain curves presented significant characteristics of dynamic recrystallization (DRX) . The temperature, strain rate and deformation degree had obvious effect on the volume fraction of recrystallized grains. Moreover, a segmented constitutive model consisted of elastic deformation stage taking elastic modulus as internal variable, work-hardening-dynamic recovery stage based on the dislocation density evolution and dynamic recrystallization stage according to the DRX kinetics was established for temperatures above and below the η-Ni₃Al_0.5Nb_0.5 solvus temperature respectively. High values of correlation coefficient (R=0.998) and average absolute relative error (AARE=2.26%) indicated that the established constitutive model could accurately characterize the hot deformation behaviour of the studied alloy.

Keyword：

ATI 718Plus superalloy; constitutive model; activation energy; dynamic recovery; dynamic recrystallization;

Received： 2018-02-01

ATI 718Plus (简称718Plus) 合金是在IN718合金成分的基础上, 通过加入Co, 降低Fe元素的含量, 以及调整Al+Ti和Al/Ti的比值, 使强化相由γ″相转变为γ′相, 同时将使用温度提高55 ℃。 该合金主要由γ′相、 η-Ni₃Ti结构的Ni₃Al_0.5Nb_0.5相 (以下简称η相) 、 MC相组成, 用于制造航空发动机涡轮盘、 叶片、 机匣、 紧固件等零部件 ^[1,2,3] 。

本构模型常用于描述合金的高温变形特性, 其中唯象型本构模型 ^[4,5] 、 人工神经网络模型 ^[6,7] 中的参量没有明确的物理意义, 并且无法解释合金在高温流动过程中的微观机制。 而机制型本构模型则从位错滑移、 晶粒尺寸、 动态再结晶等微观结构的演变机制, 预测材料的应力-应变关系 ^[8,9,10] 。 其中, 动态再结晶模型广泛应用于各种材料的高温变形行为表征中 ^[11,12,13] 。 但是通过研究发现, 该机制型本构模型在加工硬化-动态回复阶段拟合精度不高 ^[8,13] 。 Huber等 ^[14] 基于Avrami方程以再结晶体积分数为50%时的变形量ε_0.5为内变量构建了718Plus合金的动态再结晶动力学模型, 但该内变量不易通过实验数据进行确定, 且其物理意义难以进行理论描述。 Ozturk等 ^[15] 以峰值应变ε_p为临界变形条件, 分别基于Estrin-Mecking-Bergstrom模型建立了该合金的加工硬化模型, 基于Avrami方程以再结晶时间t₅₀为内变量构建了动态再结晶动力学模型, 但是, 以ε_p作为临界变形条件不够准确, 且以t₅₀为内变量预测再结晶体积分数较难控制。 此外, 鲜见针对该合金本构模型系统地研究。

本文以718Plus高温合金为研究对象, 通过热模拟压缩得到的应力-应变曲线研究合金的高温流变特性, 并建立该合金的机制型本构模型, 为后续高温塑性变形过程数值模拟奠定基础。

1 实 验

本实验所用材料为718Plus镍基高温合金棒材, 其化学成分及原始组织分别见表1和图1。 由图1可知, 718Plus合金的显微组织为等轴再结晶晶粒, 晶粒并存在大量孪晶, 晶粒尺寸约为62.5 μm。

采用线切割从原始棒材同一圆周处切取Φ10 mm×15 mm的热模拟压缩试样若干, 在Gleeble-1500D热模拟试验机上采用圆柱体单向压缩法进行轴向等温热压缩试验, 试样压缩变形量为50%、 变形温度为980～1140 ℃、 应变速率为0.001～1.000 s^-1。 压缩过程中, 试样采用真空电阻加热, 加热速率为10 ℃·s^-1, 升温至变形温度后, 保温 5 min, 以便保证试样温度分布达到均匀化。 随后在预定的变形温度和应变速率下进行等温压缩变形, 变形后立即将试样水淬, 以保留高温变形组织。

表1 718Plus高温合金化学成分

Table 1 Chemical compositions of 718Plus superalloy (%, mass fraction)

C	Cr	Mo	Nb	Al	Ti	Co	Fe	W	P	B	Ni
0.025	18.0	2.70	5.40	1.45	0.70	9.0	10.0	1.0	0.007	0.004	Bal.

图1 718Plus高温合金原始组织

Fig.1 Initial microstructure of 718Plus superalloy bar

2 结果与讨论

2.1 合金的流变特性

718Plus高温合金在不同变形条件下的应力-应变曲线如图2所示。 对比合金在不同变形温度和应变速率下的流变曲线可以发现, 变形温度、 应变速率对合金的流变应力具有显著影响。 由图2 (a) 可知, 应变速率一定时, 流变应力随着变形温度的升高而减小。 当变形温度升高时, 材料热激活作用增强, 原子间的平均动能升高, 晶体发生滑移的临界分切应力减小, 有利于位错运动和晶界滑移。 同时, 材料内部畸变储存能升高, 驱动动态回复和动态再结晶的发生, 软化作用显著, 降低材料的流动应力。 由图2 (b) 可知, 变形温度一定时, 流变应力随着应变速率的降低而减小。 当应变速率降低时, 变形时间延长, 晶体内部原子具有足够的时间进行扩散, 晶界移动性增强。 同时, 动态再结晶晶粒的形核、 长大进行得更充分, 软化作用较为显著, 材料流动应力下降。

此外, 由图2可知, 718Plus高温合金在不同条件下的应力-应变曲线在到达峰值之后出现明显的软化下降, 属于典型的动态再结晶特征。 在变形初期 (ε<ε_c) , 位错大量增殖并发生塞积和缠结, 位错密度快速增加, 加工硬化作用明显; 而动态回复的软化作用较小, 导致流变应力随应变的增加而快速升高。 随着应变的增加 (ε≥ε_c) , 动态软化机制 (动态回复和动态再结晶) 的作用逐渐增强, 加工硬化率逐渐减小, 流动应力的升高速率减缓, 流变曲线缓慢到达峰值应力; 之后, 由动态回复和动态再结晶引起的软化率大于加工硬化引起的硬化率, 动态软化行为占据主导地位, 材料流动应力逐渐下降。 随着变形量的不断增加, 动态软化率和加工硬化率最终达到动态平衡, 流变应力趋于平稳, 进入稳态流动阶段。

图2 718Plus高温合金不同条件下的真应力-真应变曲线

Fig.2 True strain-stress cures of 718Plus superalloys at different deformations

(a)

=0.01 s^-1; (b) T=1100℃

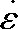
2.2 流变应力本构方程的确定

2.2.1 变形激活能

变形温度和应变速率对材料流变应力的影响, 可以采用Zener-Hollomon参数 (Z) 进行表征 ^[16] , 其表达式为:

Ζ=˙εexp(Q/RΤ)=A[sinh(ασ)]n?????????(1) Z=ε˙exp(Q/RT)=A[sinh(ασ)]n?????????(1)

式中, ˙ε 为应变速率 (s^-1) ; Q为材料的热变形激活能 (J·mol^-1) ; R为气体常数 (8.3145 J·mol^-1·K^-1) ; T为绝对温度 (K) ; A, α为材料常数; n为与应变速率敏感性指数相关联的参数。

718Plus高温合金的高温变形过程受热变形激活控制, 其流动应力与应变速率、 变形温度间的关系可用包含变形激活能Q的Arrhenius型方程表示:

˙ε=A[sinh(ασ)]nexp(-Q/RΤ)?????????(2)

为了准确描述718Plus高温合金的高温变形特性, 本研究采用峰值应变处数据构建合金的本构关系 ^[17] , 不同变形条件下的峰值应力σ_p值可在对应的应力-应变曲线上测量得到。 A可由下式计算得到:

α=β/n₁ (3)

式中, β, n₁为材料常数, 可由 ln˙ε-lnσ 以及 ln˙ε-σ 拟合曲线得到, 而n值和Q值分别由 ln˙ε-ln[sinh(ασ)] 和ln[sinh (ασ) ]-1/T拟合曲线得到, 最终计算得: Q=517.5kJ·mol^-1。

2.2.2 弹性阶段

由胡克定律可知, 在弹性变形阶段当应力低于比例极限时, 合金所受的应力σ与应变ε呈线性相关, 其表达式为:

σ=Eε (4)

式中, E=σ_e/ε_e≈σ₀/ε₀, 为弹性模量; σ_e为比例极限; ε_e为比例极限对应的应变; σ₀为屈服应力; ε₀为屈服应变。

不同变形条件下的屈服应力σ₀可以直接从应力-应变曲线上读取得到。 当变形温度T高于η相溶解温度 (T_η≈990 ℃ ^[14] ) 时, 通过图3所示拟合过程可以得到σ₀, ε₀与Z参数满足的函数关系, 分别为:

σ₀=1260.31-72.32lnZ+1.06 (lnZ) ² (5)

ε₀=1.56×10^-5Z^1.176 (6)

同理, 可以得出T<T_η时, σ₀, ε₀与Z参数之间的函数关系表达式如下:

σ₀=2830.18-142.33lnZ+1.839 (lnZ) ² (7)

ε₀=0.737-0.034lnZ+4.083×10^-4 (lnZ) ² (8)

图3 屈服应力σ0、 屈服应变ε0与Z参数的关系

Fig.3 Relationship between yield stressσ₀, yield strainε₀ and Zener-Hollomon parameter

(a) Yield stressσ₀; (b) Yield strainε₀

2.2.3 加工硬化-动态回复阶段

金属材料的流变应力受晶体内部位错密度的影响, 而晶体内部位错密度增量由加工硬化引起的位错密度增加和动态软化引起的位错密度降低决定, 其与加工硬化、 动态回复之间的关系可表示为 ^[18] :

dρ/dε_s=U-Ωρ (9)

式中, dρ/dε_s为位错密度增量; U代表加工硬化引起的位错密度增加量, 在一定的应变下, 可视为常数; Ω为动态回复系数; ρ为位错密度。

金属的流变应力与晶体内部位错密度符合Taylor关系, 其表达式为 ^[19] :

σ=αμb√ρ?????????(10)

式中, α为材料常数; μ为剪切模量; b为伯氏矢量。

当ε_s=0, ρ=ρ₀, ρ₀为初始位错密度, 相应的应力为屈服应力 σ0=αμb√ρ0 。

当dρ/dε_s=0时, ρ=ρ_sat=U/Ω, ρ_sat为加工硬化外延饱和位错密度, 相应的应力为饱和应力 σsat=αμb√ρsat=αμb√U/Ω 。

对式 (9) 积分可得:

ρ=UΩ-UΩe-Ωεs+ρ0e-Ωεs?????????(11)

将式 (10) 代入式 (11) 可得加工硬化-动态回复阶段的流变应力表达式为:

σ_WH=[σ 2sat + (σ 20 -σ 2sat ) e^-Ωε_s]^0.5 (ε_s<ε_cs) (12)

不同变形温度和应变速率下的饱和应力σ_sat可由对应的加工硬化率曲线θ (θ=dσ/dε_s) -σ得到。 Poliak和Jonas ^[20] 认为动态再结晶软化行为的发生对应于最大的能量储存和最小的耗散效率, 可由加工硬化率曲线上的拐点及其偏导 (-?θ/?σ) -σ曲线上的极小值点进行表征:

??σ(-?θ?σ)|DRX=0?????????(13)

图4为应变速率0.01 s^-1不同变形温度下合金的 (-?θ/?σ) -σ关系曲线, 从图中可以看出不同温度下-?θ/?σ数值随流变应力σ的升高先减小后增大, 曲线的极小值点即为对应加工硬化率曲线的拐点。 在图5中经过拐点作加工硬化率曲线的切线并与X轴相交, 其交点即为该条件下的饱和应力σ_sat。

图4 应变速率为0.01 s-1, 不同变形温度下-?θ/?σ与σ关系图

Fig.4 Relationship between -?θ/?σ and σ under different temperatures and strain rate of 0.01 s^-1

不同变形条件下合金的饱和应力σ_sat、 动态回复系数Ω与Zener-Hollomon参数对应关系如图6所示。

由图6可知, 变形温度高于η相溶解温度时, σ_sat, Ω与Z参数之间符合的函数关系表达可分别表示为:

lnσ_sat=-12.39+0.635lnZ-0.0053 (lnZ) ² (14)

Ω=371.62Z^-0.0613 (15)

同样地, 可分别得出低于η相溶解温度时σ_sat, Ω与Z参数之间符合的函数关系:

lnσ_sat=-24.4+1.555lnZ-0.011 (lnZ) ² (16)

Ω=2.076×10⁵Z^-0.183 (17)

2.2.4 动态再结晶阶段

当材料的塑性变形量超过临界应变ε_cs时, 在晶界、 孪晶界以及剪切带等变形缺陷较多的高能区域会首先发生动态再结晶。 尤其在高温和低应变速率下, 动态再结晶软化行为更为明显。 一般情况, 动态再结晶体积分数 (X_D) 可采用Avrami模型表示 ^[21] :

XD=1-exp[-Κd(εs-εcsεps)]nd(εs>εcs)?????????(18)

式中: ε_cs为临界应变; ε_ps为峰值应变; K_d, n_d为材料常数。 其中, 再结晶体积分数X_D与流动应力σ符合以下关系 ^[22] :

XD=σWΗ-σσsat-σss?????????(19)

式中: σ_WH为仅发生加工硬化和动态回复时的应力; σ_sat为饱和应力; σ_ss为稳态应力。 将式 (19) 代入式 (18) , 可得动态再结晶阶段的流变应力表达式:

σ=σWΗ-(σsat-σss){1-exp[-Κd(εs-εcsεps)]nd}?????????(20)

图5 应变速率为0.01 s-1, 不同变形温度下加工硬化率θ与σ的关系

Fig.5 Relationship between work hardening rate θ and σ under different temperatures and strain rate of 0.01 s^-1

图6 饱和应力σsat, 动态回复系数Ω与Z参数的关系

Fig.6 Raletionship between saturation stressσ_sat, dynamic recovery coefficientΩand Zener-Hollomon parameter

(a) Saturation stressσ_sat; (b) Dynamic recovery coefficientΩ

式中, σ_WH可由加工硬化-动态回复阶段的本构模型求解; 饱和应力σ_sat、 稳态应力σ_ss可由加工硬化率曲线 (θ-σ) 得出, 临界应力σ_c可由 (-?θ/?σ) -σ关系曲线得出, 临界应变ε_cs为临界应力σ_c所对应的应变, 可以从应力-应变曲线读取。

当T>T_η时, 峰值应变ε_ps、 稳态应力σ_ss与Zener-Hollomon参数的对应关系如图7所示。 峰值应变ε_ps与临界应变ε_cs的关系如图8所示, 经拟合可得, 其关系表达式分别为:

ε_ps=0.0113lnZ-0.349 (T>T_η) (21)

σ_ss=2148.94-117.95lnZ+1.62 (lnZ) ² (T>T_η) (22)

ε_cs=0.835ε_ps-0.021 (23)

同理可得到T<T_η时ε_ps, σ_ss与Z参数之间的函数关系如下:

ε_ps=0.0147lnZ-0.541 (T<T_η) (24)

σ_ss=32.485lnZ-1298.02 (T<T_η) (25)

将不同条件下的应力值σ, σ_WH, 饱和应力σ_sat以及稳态应力σ_ss代入式 (19) , 可以得出718Plus合金的再结晶动力学曲线, 图9为不同变形温度和应变速率下合金的再结晶动力学曲线。 对比曲线可知, 在相同的应变下, 提高变形温度或降低应变速率, 可以显著提高合金的动态再结晶体积分数。

式 (18) 中的材料常数K_d, n_d可由ln[-ln (1-X_D) ]-ln[ (ε-ε_cs) /ε_ps]曲线拟合得到。

当T<T_η时, n_d的拟合值介于1.67～2.19之间, 取其均值n_d=1.969, 对应的K_d与Zener-Hollomon参数的关系表达式为:

K_d=0.02128lnZ-0.856 (26)

同理可得到T>T_η时, n_d=1.938, K_d=0.19。

图7 峰值应变εps、 稳态应力σss与Z参数的关系

Fig.7 Relationship between peak strainε_ps, steady stressσ_ssand Zener-Hollomon parameter

(a) Peak strainε_ps; (b) Steady stressσ_ss

图8 峰值应变εps与临界应变εcs的关系

Fig.8 Relationship between peak strain ε_psand critical strain ε_cs

图9 再结晶体积分数XD与应变εs的关系

Fig.9 Relationship between recrystallized volume fractions X_Dand strain stress ε_s

图10 718Plus高温合金不同条件真应力-应变曲线实验值与预测值的对比

Fig.10 Comparison of experimental and predicted true strain-stress cures of 718Plus superalloy at different deformations

(a) T=980℃; (b) T=1020℃; (c) T=1060℃; (d) T=1100℃; (e) T=1140℃

2.2.5 本构模型的验证

图10为718Plus高温合金在不同变形条件下的试验应力-应变曲线与模型预测曲线的对比结果。 显然, 实验值与预测值整体上吻合度较高。 由图11预测应力与实验应力的相关性可知 ^[8] , 预测应力与实验应力的吻合度较高, 相关系数R为0.998, 平均相对误差AARE为2.26%。

图11 预测应力与实验应力的相关性

Fig.11 Correlation between predicted and measured flow stresses

3 结 论

1. 718Plus高温合金流动应力随应变速率的降低或变形温度的升高显著降低, 变形过程受热激活控制, 热变形激活能Q为517.5 kJ·mol^-1。

2. 718Plus高温合金的应力应变曲线具有明显的动态再结晶特征, 变形量、 变形温度以及应变速率对动态再结晶体积分数均具有显著影响。

3. 以η相溶解温度为临界点分段构建了718Plus高温合金弹性变形阶段、 加工硬化-动态回复阶段以及动态再结晶阶段的本构关系模型, 并对该模型预测能力进行了结果验证, 模型整体精度较高, 相关系数为0.998, 平均相对误差为2.26%, 能够准确表征718Plus高温合金的高温流变行为。

参考文献

[1] Kennedy R L.Allvac^? 718Plus^TM, superalloy for the next forty years [A].Loria E A.Superalloys 718, 625, 706 and Derivatives 2005 [C].Pennsylvania:TMS, 2005.1.

[2] Wang M Q, Deng Q, Du J H, Tian Z L, Zhu J.Research progress of alloy ATI 718Plus in China [J].Rare Metal Materials and Engineering, 2016, 45 (12) :3335. (王民庆, 邓群, 杜金辉, 田志凌, 朱静.ATI 718Plus合金国内研究进展 [J].稀有金属材料与工程, 2016, 45 (12) :3335.)

[3] Du J H, Wang M Q, Deng Q, Qu J L, Lü X D, Bi Z N.The research on the mechanism of the influence on microstructure and properties of alloy GH4169Plus by phosphorus [J].Journal of Iron and Steel Research, 2011, (S2) :209. (杜金辉, 王民庆, 邓群, 曲敬龙, 吕旭东, 毕中南.磷对GH4169Plus合金组织及性能影响机理的研究 [J].钢铁研究学报, 2011, (S2) :209.)

[4] Luo R, Cheng X N, Xu G F, Guo S, Zheng Q, Zhu J J.Constitutive modeling for elevated temperature flow behavior of Fe-20Cr-30Ni-0.6Nb- 2Al-Mo alloy [J].Chinese Journal of Rare Metals, 2017, 41 (2) :132. (罗锐, 程晓农, 徐桂芳, 郭顺, 郑琦, 朱晶晶.新型Fe-20Cr-30Ni-0.6Nb-2Al-Mo合金的热变形行为及本构模型 [J].稀有金属, 2017, 41 (2) :132.)

[5] Du Y, Zhao Y X, Yu Z Q, Li X L.Constitutive equation of electroplastic effect for 2060-T8 Al-Li alloy [J].Journal of Plasticity Engineering, 2017, 24 (1) :133. (杜引, 赵亦希, 于忠奇, 李喜林.2060-T8铝锂合金电致塑性本构方程 [J].塑性工程学报, 2017, 24 (1) :133.)

[6] Wang J, Chu Z, Zhang Q.A comparative study of two high-temperature constitutive models of 38MnVS6 microalloyed forging steel [J].Journal of Material Engineering, 2014, (2) :81. (王进, 褚忠, 张琦.38MnVS6非调质钢两种高温本构模型的对比 [J].材料工程, 2014, (2) :81.)

[7] You X L, Hua J S, Yao W, Liu Y Y, Li J, Wang K.Comparison on two kinds of constitutive model for fine grain TC4 titanium alloy [J].Transactions of Materials and Heat Treatment, 2015, 36 (8) :237. (尤雪磊, 华建社, 姚渭, 刘莹莹, 李洁, 王坤.细晶TC4钛合金两种本构模型的对比 [J].材料热处理学报, 2015, 36 (8) :237.)

[8] Lin Y C, Chen X M, Wen D X, Chen M S.A physically-based constitutive model for a typical nickel-based superalloy [J].Computational Materials Science, 2014, 83 (2) :282.

[9] Laasraoui A, Jonas J J.Prediction of steel flow stresses at high temperatures and strain rates [J].Metallurgical Transactions A, 1991, 22 (7) :1545.

[10] Sommitsch C, Mitter W.On modelling of dynamic recrystallisation of fcc materials with low stacking fault energy [J].Acta Materialia, 2006, 54 (2) :357.

[11] Xiao Z B, Huang Y C, Liu Y.Physically-based constitutive model for high temperature deformation of electromagnetic casted 35CrMo steel [J].Heat Treatment of Metals, 2017, 42 (1) :1. (肖政兵, 黄元春, 刘宇.基于微观机制的电磁铸造35CrMo钢的高温流变本构方程 [J].金属热处理, 2017, 42 (1) :1.)

[12] Chen F, Feng G, Cui Z.New constitutive model for hot working [J].Metallurgical and Materials Transactions A, 2016, 47 (3) :1229.

[13] Xu Y, Hu L, Sun Y.The flow behavior and constitutive equations in isothermal compression of 7050 aluminum alloy [J].Materials Science and Engineering A, 2012, 542 (18) :79.

[14] Huber D, Stotter C, Sommitsch C, Mitsche S, Poelt P, Buchmayr B, Stockinger M.Microstructure modeling of the dynamic recrystallization kinetics during turbine disc forging of the nickel based superalloy Allvac 718Plus [A].Reed R C, Green K A, Caron P, Gabb T, Fahrmann M G, Huron E S, Woodard S A.Superalloys 2008 [C].Pennsylvania:TMS, 2008.855.

[15] Ozturk U, Cabrera J M, Calvo J.High Temperature Deformation of Inconel 718Plus^TM [J].Journal of Engineering for Gas Turbines and Power, 2017, 139 (3) :1.

[16] Gong Q J, Yang M, Liang Y L, Xu X, Zhang S W.Hot formability and dynamic recrystallization behavior of new high performance aluminum alloy 211Z-X [J].Chinese Journal of Rare Metals, 2018, 42 (1) :36. (龚乾江, 杨明, 梁益龙, 徐祥, 张世伟.211Z-X新型高强韧铝合金热成形及动态再结晶行为研究 [J].稀有金属, 2018, 42 (1) :36.)

[17] Yang X M, Guo H Z, Liang H Q, Yao Z K, Yuan S C.Flow behavior and constitutive equation of Ti-6.5Al-2Sn-4Zr-4Mo-1W-0.2Si titanium alloy [J].Journal of Materials Engineering and Performance, 2016, 25 (4) :1347.

[18] Bergstrom Y.A dislocation model for the stress-strain behavior of polycrystalline α-Fe with special emphasis on the variation of the densities of mobile and immobile dislocations [J].Materials Science and Engineering, 1970, 5 (4) :193.

[19] Dong D, Chen F, Cui Z.A physically-based constitutive model for SA508-III steel:modeling and experimental verification [J].Materials Science and Engineering A, 2015, 634:103.

[20] Poliak E I, Jonas J J.A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization [J].Acta Materialia, 1996, 44 (1) :127.

[21] Lin Y C, Chen M S, Zhong G J.Prediction of 42CrMo steel flow stress at high temperature and strain rate [J].Mechanics Research Communications, 2008, 35 (3) :142.

[22] Kong L X, Hodgson P D, Wang B.Development of constitutive models for metal forming with cyclic strain softening [J].Journal of Materials Processing Technology, 1999, s89-90 (8) :44.