异常检测系统的漏洞分析
刘星宝1, 2，蔡自兴1
(1. 中南大学 信息科学与工程学院，湖南 长沙，410083；
2. 湖南商学院 现代教育技术中心，湖南 长沙，410205)
摘 要：针对阴性选择算法生成的异常检测系统存在大量漏洞的问题，提出一种能够探测系统全部漏洞的非检测模式漏洞探测算法(EHANDP)。首先，指出目前检测系统漏洞探测算法(EHASP)的不完备性；然后，利用问题空间中的串模式证明空间中个体成为漏洞的充分必要条件，并提出探测系统漏洞的完备性算法EHANDP，能够找出给定系统的全部漏洞是该算法的主要特点。实验中采用随机数据集和人工数据集比较2种漏洞探测算法。研究结果表明：在相同的实验环境下，EHANDP算法与EHASP相比不仅有相同的计算复杂度，而且有更强的探测能力。
关键词：人工免疫系统；阴性选择算法；漏洞；异常检测
中图分类号：TP311 文献标识码：A 文章编号：1672-7207(2009)04-0986-07
Properties assessments of holes in anomaly detection systems
LIU Xing-bao1, 2, CAI Zi-xing1
(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;
2. Center of Modern Education Technology, Hunan Business College, Changsha 410205, China)
Abstract：A novel exploring holes algorithm based on non-detector pattern (EHANDP) was proposed for holes existing in anomaly detection system generated by negative selection algorithm. Incompleteness of current exploring holes algorithm grounded on self pattern (EHASP) was pointed out. And then the sufficient and necessary condition for individuals to become holes was proven using the string patterns in problem space, and an exploring holes algorithm named EHANDP which could find all holes of a given detection system was proposed. The above two algorithms were compared using random dataset and artificial dataset. The results show that the exploring capability of EHANDP algorithm is greater than that of EHASP although they have the same computational complexity.
Key words: artificial immune systems; negative selection algorithm; hole; anomaly detection
人工免疫系统是受免疫学启发，模拟生物免疫系统功能、原理和模型来解决复杂问题的自适应系统。其研究成果涉及计算机安全、工程优化、数据挖掘、控制、故障诊断等许多领域，已经成为继神经网络、模糊逻辑和进化计算后人工智能的又一研究热点[1]。在复杂免疫系统的诸研究分支中，阴性选择、克隆选择和免疫网络是关注度最高的3个研究分支[2-3]。
阴性选择机制能够准确区分自体和异体、保障免疫系统的正常运转，是免疫系统的重要构成[4]。Forrest等[5]建立了阴性选择算法框架，并成功应用于异常检测系统。目前，阴性选择原理成为人工免疫领域的研究热点[6]。类似自然免疫系统，以阴性选择算法为基础得到的异常检测系统能够很好地区分“自体/异体”，完成保护数据的任务[5, 7-8]。但是，状态空间中存在不能被检测系统识别的异体，此类异体的存在降低了系统的检测精度[9-10]。同样的问题也存在于生物免疫系统中，如病原体总是向漏洞的方向进化，以增加免疫系统的检测难度。生物免疫系统采用MHC机制来解决漏洞问题[11]。据此，Hofmeyr[12]提出采用多重表示模拟生物免疫系统的MHC机制，以减少漏洞的数量。该方法使用同一种匹配规则，但运用不同的模式表示法，其最大缺点是对系统稳定性有较大影响。张衡 等[13]以r-连续位匹配准则为基础，提出一种匹配阀值可变的阴性选择算法。该算法的核心是通过调整匹配阈值来降低漏洞数量，但没有从理论上分析影响漏洞的因素。Stibor等[14]提出了探测系统漏洞的算法，但其只能探测到系统的部分漏洞，而非全部漏洞。
漏洞的存在及其规模取决于自体集合的模式结构和训练自体集合所采用的匹配规则[6]。基于此，本文作者利用自体集和检测器集在状态空间中的相互关系，应用实例证明Stibor漏洞探测算法的不完备性，然后提出探测检测系统漏洞的非检测模式漏洞探测算法(EHANDP算法)，证明该算法的完备性；最后，应用随机数据集和人工数据集对EHANDP算法进行全面测试，同时考察系统中影响漏洞规模的因素。
1 问题定义
在阴性选择领域内，采用二进制编码[6, 8-9, 12, 14]。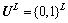
表示长为L字符串向量空间，S表示自体空间向量集合，N表示异体空间向量集合，D表示检测器空间向量集合。阴性选择算法就是在空间
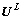中，根据某种匹配准则训练自体集合S以生成检测器集合D，从而建立起从自体空间到异体空间的映射关系，其基本算法为[11]：
a. 定义被保护数据为集合S，编码长度为L；
b. 依据匹配准则训练自体集，生成检测器集合D；
c. 用D探测被保护信息，若有异常，则发出响应。
训练自体集合采用的匹配准则对检测系统有很大的影响，不同的匹配准则甚至相同匹配准则的不同阀值r对检测性能的影响都不一样。r-连续位匹配准则(r-contiguous bits matching)、r-块匹配准则(r-chuck matching rule)、汉明匹配准则(Hamming matching rule)及其变种是目前使用最多的准则[6]，但是，不论应用何种准则，生成的检测系统都存在漏洞[14]。这些漏洞不能被检测系统识别，它们的存在降低了系统的检测率，增加了系统的不安全因素，因此，深入研究漏洞的性质对提高异常检测系统的安全性尤为重要。为了方便，给出以下定义。
定义1 长为L二进制字符串X=x1x2…xL和Y=y1y2…yL满足r-连续位匹配，当且仅当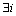
≤
，使得
j=i, i+1, …, i+r-1；若X是长为L的二进制向量，Y是二进制m×L矩阵，则存在整数t(1≤t≤m)和i(1≤i≤L-r+1)，满足xj=Y(t, j)，其中：j=i, …, i+r-1。
定义2 设集合D是自体集合S应用r-连续位匹配生成的检测器。若异体x不能与检测器集合D中的任何个体匹配，则x称作检测系统的漏洞。
在问题空间中自体集合与异体集合的边缘通常是不规则的，这是漏洞产生的重要原因。设自体s1和s2分别如下：
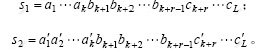
依据s1和s2，构造个体h1和h2：
依据r-连续位匹配准则，h1和h2不可能被系统中的任意检测器识别，即h1和h2成为系统的漏洞。
设自体集有如下形式：
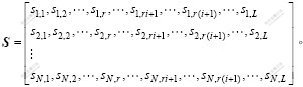
根据r-连续位匹配将其分解为L-r+1层模式集合
。
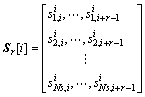其中：i=1, 2, …, L-r+1；r为模式集合中个体的长度；i为模式集合的层次；Ns为S集合的规模。以上面的L-r+1层模式集合为基础，Stibor等[14]提出检测系统漏洞探测算法(EHASP算法)。
若自体集合S={10010，11010，01101，00110}，取匹配阀值r=3，EHASP生成漏洞的过程如图1所示。
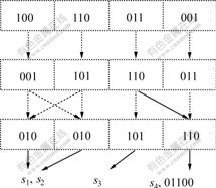
图1 漏洞的生成过程
Fig.1 Process of generating holes
从图1可以看出，漏洞个体与自体集合密切相关，两者在结构上存在相同的模式。实际上，检测系统是否存在漏洞取决于自体模式集合的内部结构和生成检测系统使用的匹配准则。自体模式内部结构相似度越高，匹配粒度越小，漏洞的数目就越多。
2 漏洞分析
2.1 基于非检测集模式的漏洞探测算法
Stibor[14]提出探测检测系统漏洞的探测算法检测到的个体都是系统的漏洞，但没有说明该算法生成的集合是否包括了检测系统的全部漏洞。通过定理1和示例可以证明该EHASP算法是空间个体成为漏洞的必要而非充分条件。
定理1 以自体模式集为基础，应用EHASP探测到的个体均是检测系统的漏洞。
证明 在L维向量空间中，检测系统的自体集合S通过r-连续位匹配生成检测器集合D，H是EHASP通过自体集合S得到的漏洞集合。假设H中存在个体x能被D检测到，则D中至少存在1个检测器个体d与x满足r-连续位匹配，即存在i(1≤i≤L-r+1)满足dj=aj，j=i, …, i+r-1。根据x的生成算法，x的全部长为r的模式都来自于相应层次的自体模式集，即在自体集合S中存在自体s和d满足r-连续位匹配，而这与d是检测器矛盾。
定理1说明，以自体模式集合为基础，应用EHASP探测到的个体都是检测系统的漏洞。通过例1证明EHASP不能探测出检测系统的全部漏洞。
例1 设S={110，010}，连续位匹配阀值r=2。按照连续位匹配准则生成的检测器集合为：
D={000，001，100，101}。
按照EHASP，探测到的检测系统漏洞集合H=?。但是，个体h=011不能被D识别，是检测系统的漏洞，因此，EHASP不是完备的漏洞探测算法。
为了能够探测到检测系统的全部漏洞，以模式集为基础寻求完备的漏洞探测算法。设EHASP以自体集合S为基础探测到的漏洞集合H，其长为r的模式集合为
Hr[i], i=1, 2, …, L-r+1。
设h∈H，h中2个连续的模式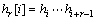
与
显然满足
。
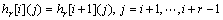为准确描述hr[i]和hr[i+1]之间的特殊匹配关系，引入新的定义。
定义3 长为r的字符串h1, h2, …, hn满足有序交叉匹配，当且仅当hi的后r-1位和hi+1的前r-1位对应相等，i=1, 2, …, r-1，记作1, h2, …, hn>。
定义4 设hi=i1hi2…hir，i=1, …, n且满足有序交叉匹配，那么由h1, h2, …, hn组合得到的长为r+n-1个体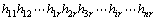
称作有序交叉匹配串，记作
。
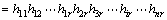从空间结构上看，自体集合、检测器集合与漏洞集合的第i层(i∈{1, 2, …, L-r+1})模式集Sr[i]，Dr[i]和Hr[i]都属于Ur空间中的向量集合。令
Cr[i]=Ur-Dr[i]，
那么，
。
对任意长为r的向量p?Cr[i]，它可能属于自体模式或者漏洞模式。下面考虑Cr[1]，Cr[2]，…，Cr[L-r+1]根据交叉匹配原则生成的长为L的个体具有的性质。
定理2 D是自体集合S依据r-连续位匹配准则生成的检测器集合，Ur是r维向量空间，Dr[i]是检测器D的第i层模式集合，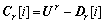
，则
系列模式集合根据有序交叉匹配原则生成的个体长为L的集合记作SH，则H=SH-S是检测系统的漏洞集，并且H包含了检测系统的全部漏洞。
证明 设H是Cr[1]，Cr[2]，…，Cr[L-r+1]根据有序交叉匹配原则生成的长为L的个体集合。对任意的h∈H，若h能被检测器D识别，则D中至少存在1个检测器个体d与h满足r-连续位匹配，也就是说，存在正整数i(1≤i≤L-r+1)，使得
，
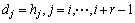即
。
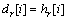并且
，
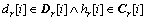于是，
。
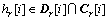这与
相矛盾。也就是说，检测器D不能检测到H中的任意个体，而H又非自体集合，所以，H是检测系统的漏洞集合。
另一方面，若检测系统中存在漏洞a，且
。即a中存在长为r的模式不属于Cr[i], i=1, …, L-r+1，不妨设该模式为a的第i层模式ar[i]。根据，那么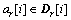
，也就是说，D中至少存在1个检测器个体d，其第i层模式dr[i]=ar[i]。即
。
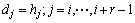于是，d和a满足r-连续位匹配，a能够被检测器D识别，这与a是漏洞的假设相矛盾，即H中包含了检测系统的全部漏洞。
定理2表明，以Cr[i], i=1, …, L-r+1为基础，根据有序交叉匹配原则探测到的H集合是检测系统的漏洞集合，并且包含了检测系统的全部漏洞。探测检测系统漏洞的具体过程如下：
a. 训练自体集合S，得到合格的检测器集合D；
b. 依据r-连续位匹配准则将D分解为个体长为r的L-r+1个模式集合：Dr[1], Dr[2], …, Dr[L-r+1]。
c. 在r维状态空间Ur中求出Dr[i]的互补模式集合Cr[i]=Ur-Dr[i], i=1, 2, …, L-r+1。
d. i=1，若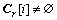
，取
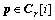，并令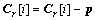
。
e. 在i+1层模式集合中，找出与p有序交叉匹配的模式结构，若该层模式集合中没有模式与p有序交叉匹配，则返回步骤c。
若该层模式集合中只有1个模式x与p有序交叉匹配，则将x的末尾元素置于p的末尾，i=i+1。转到步骤d。
若该层模式集合中有x1和x2 2个模式与p有序交叉匹配，将x1的末尾元素置于p的末尾并记为p1； 将x2末尾元素置于p的末尾并记为p2，令i=i+1。转到步骤e。
f. 若i=L-r+2，则将新生成的、长度为L的字符串置入集合Hole_ND中。
g. 去掉集合Hole_ND中和自体集合S重复的元素，得到漏洞集合H。
例2具体地说明了漏洞探测算法EHANDP探测检测系统漏洞的过程。
例2 设自体集合S = {01001, 00001, 10100, 11101}，由自体集合S根据算法EHASP探测到的系统漏洞集合为：
H1= {10101, 11100}。
依据r连续位匹配准则生成的检测器集合D为：
D= {00110, 00111, 01110, 01111, 10010, 10011, 11010, 11011}。
D的长为r的模式集分别为：
D3[1]={001,011,100,110};
D3[2]={010,011,111,001,101};
D3[3]={110,111,011,010}。
D3[1]，D3[2]和D3[3]在U3向量空间中相应的补模式集分别为：
C3[1]={000,010,101,111};
C3[2]={000,100,110};
C3[3]={000,001,100,101}。
C3[1]，C3[2]和C3[3]根据EHANDP算法得到的漏洞集合为：
H2 = {00000, 01000, 10101, 11100}。
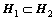，表明算法EHANDP比EHASP有更强的探测能力。
2.2 计算复杂性分析
首先考虑算法EHASP。当自体的模式集只有2层即L-r=1的情况，从第1模式集合Sr[1]中取1个个体p，在p后加“0”构成p0，取其后r位，得到tp0；在p的末尾加“1”构成p1，取其后r位，得到tp1；在第2层中搜索与tp0或者与tp1相同的个体。而tp0或者tp1中有1个是自体集合的子串，不需要查找，因此，在无序搜索算法平均时间耗费为Ns/2。在最差的情况下，每一层都匹配成功，也就是说，第2层匹配结束后得到2个个体，搜索次数为Ns/2；第3层匹配结束后得到22个个体，搜索次数为2×Ns/2，第L-r+1层匹配节结束后得到2L-r-1个个体，搜索次数为2L-r-1×Ns/2。第1层共有Ns个个体，所以，算法总的匹配次数为：
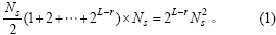
在最好的情况下就是系统中不存在漏洞。算法在第2层模式匹配结束后得到1个个体，搜索次数为Ns/2，在第3层匹配结束后仍得到1个个体，搜索次数为Ns，第L-r+1层匹配节结束后得到1个个体，搜索次数为Ns/2，所以，算法总的搜索次数为：
对于算法EHANDP，时间复杂度分析和EHASP的分析类似，在最差情况下，复杂度为：
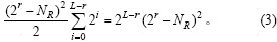
在最好情况下，复杂度为：
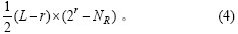
3 漏洞算法的仿真分析
对EHASP和EHANDP进行仿真，分析比较相同条件下EHASP和EHANDP生成漏洞的规模，然后，分析r-连续位匹配阀值、自体集合内部模式结构对漏洞规模的影响。
3.1 数据采集
为揭示数据集内部模式结构对漏洞规模的影响，实验采用随机数据集和人工数据集。前者采用Mat lab R2007b平台产生；人工数据集采用香蕉数据集，该数据集包含400行2列实数表示的数据，试验中被转换成400行16列的二进制矩阵。
3.2 实验过程
3.2.1 2种算法的漏洞规模比较
采用随机数据集和人工数据集，规模为Ns=400，个体长度L=16；r-连续位匹配阀值为9。针对2种数据集分别运行EHASP和EHANDP，生成漏洞H1和H2。实验步骤如下：
a. 采集人工数据集和随机数据集作为自体集；
b. 以自体集合为基础，根据EHASP生成漏洞集合H1，令h1=# H1。“#”表示集合的势；
c. 依据r连续位匹配准则生成检测器集合D；
d. 以检测器集合D为基础、根据EHANDP探测漏洞集合H2，令h2=# H2。；
e. 重复实验100次，统计数据。
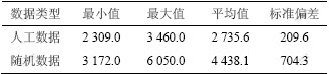
通过以上实验步骤得到的漏洞的统计性质如表1所示。
表1 漏洞的统计性质
Table 1 Statistical properties of holes
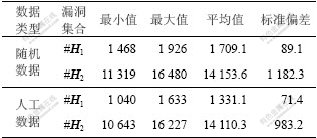
从表1可知，2种数据集下独立运行100次，算法EHANDP生成漏洞数远比EHASP得到的漏洞数多，表明前者比后者的探测能力强，如图2~4所示。
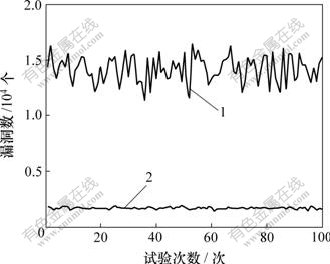
1—EHANDP；2—EHASP
图2 基于随机数据集得到的漏洞
Fig.2 Size of hole sets generated using random dataset
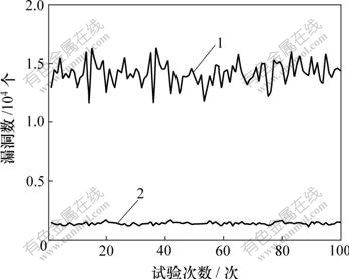
1—EHANDP；2—EHASP
图3 基于人工数据集得到的漏洞
Fig.3 Size of holes generated through artificial datasets
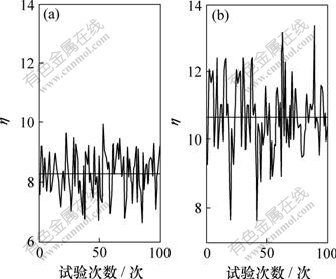
(a) 人工数据集；(b) 随机数据集
图4 算法EHASP和算法EHANDP在不同数据集下的表现
Fig.4 Performance of EHASP and EHANDP based on random and artificial dataset
h1和h2的关系如图4所示，其中
。可见，在人工数据集下，h=6.5~10.2，均值为8.3；当使用随机数据集时，h的变化幅度增加，h=7.7~13.4，均值也达到10.8。
3.2.2 连续位匹配阀值对漏洞数的影响
本次实验以随机数据集和人工数据集为基础，测试匹配阀值r对漏洞数的影响。自体集规模为400行16列，匹配阀值r从6到16，步长为1，应用EHANDP生漏洞集合。当r取6，7和16时，系统漏洞接近于0，在r=8时漏洞最多，如图5所示。
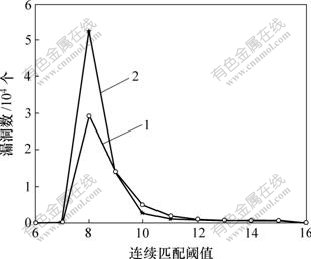
1—人工数据集；2—随机数据集
图5 匹配阀值r对系统漏洞的影响
Fig.5 Matching threshold on impact of holes
3.2.3 自体内部结构变换对漏洞规模的影响
在自体集合400行16列、r=10时，针对随机数据集和人工数据集应用算法EHANDP探测系统的漏洞。从图6和表2可以看出人工数据集生成的漏洞比随机数据集得到的漏洞少，这说明自体集合内部的模式结构影响漏洞数。
表2 不同数据集下的系统漏洞数比较
Table 2 Comparison of holes explored in two dataset
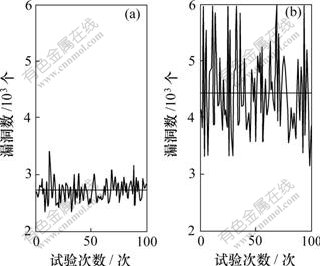
(a) 人工数据集；(b) 随机数据集
图6 数据集对漏洞数的影响
Fig.6 Effect of datasets on holes
3.3 实验结果分析
自体集合内部的模式结构是影响漏洞数的重要因素，EHASP以自体集合中长为r的模式集为基础生成检测系统的漏洞集合H1，但H1只是检测系统中漏洞集合的一部分，没有包含全部的漏洞。当随机自体集为400个个体时，EHASP得到的平均漏洞数1709.1；在相同的实验环境下，EHANDP得到的平均漏洞数为14 153.6，远远高于前者(如图3所示)。当以人工数据为基础重复上面的实验时，EHASP探测到的漏洞数为1 331.1，EHANDP探测得到的漏洞数为14 110.3，仍然高于前者(如图3所示)。从图4可见，在随机数据集得到的平均值为8.3，人工数据下得到的平均值为10.8。因此，EHASP得到的漏洞集合只是检测系统漏洞集合的一小部分，而非全部。
当r≤7和r=16时，漏洞数近似为0，前者是因为在该阀值下，模式空间中最多包含27=128个模式，这些模式一部分构成了检测器集合，该部分对漏洞没有贡献；状态空间中的另外一部分模式构成了自体集合，这些模式集合要构成检测系统的漏洞必须满足：在10(L-r+1)个模式集合中，相邻层次的模式集合有有序交叉匹配的个体；不能是自体本身。这2个条件非常苛刻，使得模式集“组装”出漏洞个体的概率很小，因此，在r≤7时漏洞数很少；在r=16时，匹配阀值r和个体编码长度L相等，虽然模式集合的状态空间很大(216=65 536), 但模式集只有1层，这使有序交叉匹配得到的个体都是自体，因此，漏洞数近似为0。实验3则从自体模式本身出发，探讨不同模式集对漏洞的影响。在Ns=400，L=16，r=10时，以随机数据集为基础，由EHANDP得到的漏洞的均值为4 438.1，而以人工数据集为基础得到的漏洞的均值为2 735.6，小于前者。这是人工数据集在状态空间中的形状更规则所致。
4 结 论
a. 分析了Stibor漏洞探测算法，证明该探测算法只能够探测到检测系统的部分漏洞，用实例指出该算法不能探测到检测系统的全部漏洞。
b. 依据连续位匹配准则将自体集分解为多层模式集合，阐明了自体模式集合、检测器模式集合在空间结构上的关系，据此给出了检测系统漏洞存在的充分必要条件，并予以证明。
c. 提出完备的漏洞探测算法。在不增加计算复杂性的情况下，该算法的探测能力更强。
参考文献：
[1] Emma H A, Timmis J. Application areas of AIS: The past, the present and the future[J]. Applied Soft Computing, 2008, 8(1): 191-201.
[2] 李彦斌, 李存斌, 杨尚东. 基于免疫遗传算法改进DFNN模型及其应用[J]. 中南大学学报; 自然科学版, 2008, 39(2): 345-349.
LI Yan-bin, LI Cun-bin, YANG Shang-dong. A new DFNN improved by artificial immune-genetic hybrid algorithm and its application[J]. Journal of Central South University: Science and Technology, 2008, 39(2): 345-349.
[3] Dasgupta D, Zhou J, Gonzalez F, et al. Artificial immune system(A IS) research in the last five years[C]//Proceedings of the 2003 Congress on Evolutionary Computation. Canberra: IEEE, 2003: 123-130.
[4] Garrett S M. How do we evaluate artificial immune systems[J]. Evolutionary Computation, 2005, 13(2): 145-178.
[5] Forrest S, Perelson A S, All L, et al. Self-nonself discrimination in a computer[C]//Proceedings of IEEE Symposium on Research in Security and Privacy, Oakland: IEEE Press, 1994: 202-212
[6] Zhou J, Dasgupta D. Revisiting negative selection algorithms[J]. Evolutionary Computation, 2007, 15(2): 223-251.
[7] Dasgupta D, González F. An immunity-based technique to characterize intrusions in computer networks[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(3): 281-291
[8] Esponda F, Forrest S, Helman P. A formal framework for positive and negative detection schemes[J]. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics, 2004, 34(1): 357-373.
[9] D'haeseleer P, Forrest S, Helman P. An immunological approach to change detection: algorithm, analysis and implications[C]// Proc of the IEEE Symposium on Security and Privacy, Los Alamitos: IEEE Computer Society Press, 1996: 132-143.
[10] D'haeseleer P. An immunological approach to change detection: Theoretical results[C]//Proceedings of the 9th IEEE Computer Security Foundations Workshop. IEEE Computer Society Press, 1996: 132-143.
[11] 龙振洲. 医学免疫学[M]. 北京: 人民卫生出版社, 1995.
LONG Zhen-zhou. Medical Immunology[M]. Beijing: People’s Medical Press, 1995.
[12] Hofmeyr S A. An immunological model of distributed detection and it s application to computer security[D]. Albuquerque: Department of Computer Sciences, University of New Mexico, 1999.
[13] 张 衡, 吴礼发, 张毓森, 等. 一种r可变负选择算法及其仿真分析[J]. 计算机学报, 2005, 28(10): 1614-1619.
ZHANG Heng, WU Li-fa, ZHANG Yu-sen, et al. An algorithm of r-adjustable negative selection algorithm and its simulation analysis[J]. Chinese Journal of Computers, 2005, 28(10): 1614-1619.
[14] Stibor T, Mohr P, Timmis J. Is negative selection appropriate for anomaly detection[C]//GECCO’05. Washington D. C, 2005: 321-328.
收稿日期：2008-09-05；修回日期：2008-11-25
基金项目：国家自然科学基金资助项目(90820302, 60234030, 60805027)；国家基础研究项目(A1420060159)；国家博士点基金资助项目(200805330005)
通信作者：刘星宝(1977-)，男，山东临沂人，博士研究生，讲师，从事人工免疫系统等研究；电话：13723874826；E-mail: liuxb0608@gmail.com
