网络首发时间: 2013-12-27 16:41

稀有金属 2014,38(02),277-282 DOI:10.13373/j.cnki.cjrm.2014.02.016

TiCl₄-CH₂Cl₂体系的气液平衡计算及应用

向小艳 王学文 王明玉

中南大学冶金与环境学院

摘 要：

采用MOSCED模型, 计算得到TiCl4-CH2Cl2二元系中TiCl4和CH2Cl2的无限稀释活度系数分别为1.151和1.114。并根据此数值, 采用Wilson模型, 计算了TiCl4-CH2Cl2二元系的活度系数。结果表明, TiCl4的活度系数随混合物中TiCl4的摩尔分数的增大而减小, CH2Cl2的活度系数随混合物中TiCl4的摩尔分数的增大而增大。采用试差法根据相平衡原理及TiCl4-CH2Cl2二元系的活度系数计算得到了TiCl4-CH2Cl2二元系的汽液平衡数据, 并绘制了TiCl4-CH2Cl2二元系的T-x-y图和y-x图, 其误差为10%左右。TiCl4-CH2Cl2二元系的汽液平衡数据表明, TiCl4和CH2Cl2混合物的初步分离可以通过蒸馏实现, 而要实现深度分离则需采用精馏的方法, 分离所需的理论塔板数为4。TiCl4-CH2Cl2二元系的无限稀释活度系数和拉曼光谱表明, TiCl4和CH2Cl2混合不形成共沸物, 混合过程中没有新化合物生成, 只是简单的溶解。

关键词：

TiCl4-CH2Cl2二元系;MOSCED模型;Wilson模型;活度系数;汽液平衡;

中图分类号： O642.42

作者简介：向小艳 (1982-) , 男, 湖南怀化人, 博士研究生, 研究方向:冶金物理化学、冶金废渣处理;;王学文, 教授;电话:0731-88830247;E-mail:wxwcsu@163.com;

收稿日期：2013-08-19

基金：国家自然科学基金项目 (51104186) 资助;

Vapor-Liquid Equilibrium Calculation and Application of TiCl₄-CH₂Cl₂ System

Xiang Xiaoyan Wang Xuewen Wang Mingyu

School of Metallurgy and Environment, Central South University

Abstract：

The limiting activity coefficient for binary systems of TiCl4-CH2Cl2was estimated by MOSCED model, and the value was 1. 151 and 1. 114 respectively for TiCl4and CH2Cl2. According to the limiting activity coefficient, the activity coefficient of TiCl4-CH2Cl2system was calculated by Wilson model. The results showed that the activity coefficient of TiCl4decreased as the mole fraction of TiCl4in the mixture increased, but the activity coefficient of CH2Cl2increased as the increase of mole fraction of TiCl4in the mixture. According to activity coefficient and theory of phase equilibrium, vapor-liquid equilibrium data of TiCl4-CH2Cl2system was computed by try and error method, and the error was about 10%. Meanwhile, the phase diagram of T-x-y and y-x were drawn. The vaporliquid equilibrium data indicated that the prefractionation of TiCl4and CH2Cl2could be reached by distillation, and the further separation could be achieved by rectification. The theoretical plate number of rectifying column for further separation of TiCl4and CH2Cl2was 4. The Raman spectra and limiting activity coefficient of TiCl4-CH2Cl2system showed that there was no azeotrope and new species generated when titanium tetrachloride mixed with dichloromethane.

Keyword：

binary systems of TiCl4-CH2Cl2; MOSCED model; Wilson model; activity coefficient; vapor-liquid equilibrium;

Received： 2013-08-19

钛及钛合金广泛应用于航天、航空、车辆工程、生物医学工程等各个领域^{［1 － 2］}, 而海绵钛是制造钛及钛合金的重要原料。而氯化法生产海绵钛的过程中会产生大量的沉淀泥浆, 其质量占到粗Ti Cl₄总量的3%~ 5%^［3］, 沉淀泥浆中Ti Cl₄含量在50% ~ 60% 。目前工业生产上, 沉淀泥浆中的Ti Cl₄还无法回收, 普遍采用水冲的方式来处理, 这不仅造成大量的Ti Cl₄损失而且增加沉重的环保压力。中南大学王学文等^［4］采用CH₂Cl₂为提取剂可有效回收沉淀泥浆中的Ti Cl₄。CH₂Cl₂与Ti Cl₄可以任意比例互溶, 常压下两者沸点相差96 ℃^{［5 － 6］}, 可通过蒸馏初步分离, 但Ti Cl₄-CH₂Cl₂混合液的蒸馏分离缺乏理论指导和依据。研究表明^{［7 － 8］}, 对于二元系混合物, 其汽液平衡数据可由无限稀释的活度系数计算。普通二元系的无限稀释活度系数可以通过实验测定, 但对于一些特殊体系, 如Ti Cl₄-CH₂Cl₂二元系, 由于体系中组分在测量条件下极不稳定, 给实验测定带来极大困难。因此, 二元系无限稀释活度系数的计算具有十分重要的意义, 为此人们提出了许多计算模型和方程^{［9 ～ 12］}用于计算二元系溶液的无限稀释活度系数。其中, MOSCED模型 ( modified separation of cohesive ener-gy density model) , 在计算非极性二元系的无限稀释活度系数时具有很高的准确度。

本文采用MOSCED模型计算Ti Cl₄-CH₂Cl₂二元系的无限稀释活度系数, 并采用Wilson模型计算其活度系数, 并推导Ti Cl₄-CH₂Cl₂二元系的气液平衡数据, 为Ti Cl₄-CH₂Cl₂混合液的蒸馏分离提供理论指导和依据。

1 Ti Cl4-CH2Cl2二元系的活度系数计算

1. 1 MOSCED模型概述

采用的MOSCED模型是规则溶液理论的拓展, 对于二元混合溶液组分2 溶于组分1 的无限稀释活度系数, 其计算公式为:

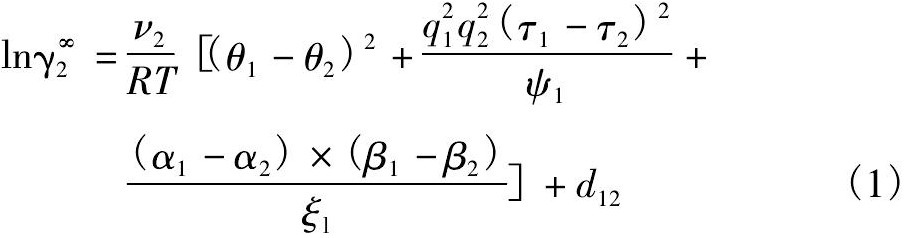
式中 ν₂为组分2 的摩尔体积, cm³·mol^{－ 1}; θ₁, θ₂为物质1 和2 的分散度参数; q为物质的感应参数; τ, α 和 β 分别为物质的极性参数、酸度和碱度参数; ψ 和 ξ 为物质的不对称参数; d₁₂为体系组合项修正系数。

1. 2 Ti Cl4-CH2Cl2二元系的无限稀释活度系数

由MOSCED模型计算并参考相应文献[12 -13], 得出Ti Cl₄-CH₂Cl₂二元体系20 ℃时的各项参数如表1 所示。

由表1 及式 ( 1 ) , 可计算出20℃ 下Ti Cl₄-CH₂Cl₂二元体系的无限稀释活度系数如表2 所示。

1. 3 Ti Cl4-CH2Cl2二元系活度系数

根据Wilson模型^［14］, 对于Ti Cl₄-CH₂Cl₂二元系, 活度系数 ( γ₁, γ₂) 的表达式为 ( 下标1 代表Ti Cl₄, 2 代表CH₂Cl₂) :

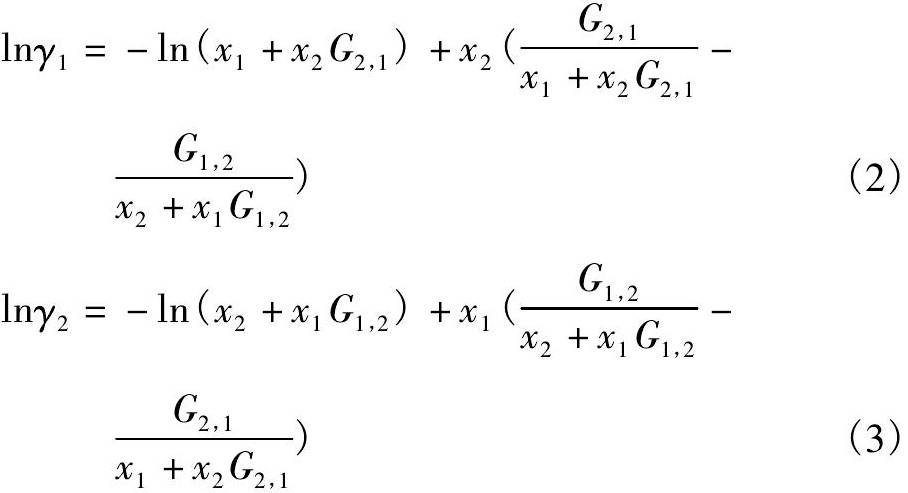
其中:

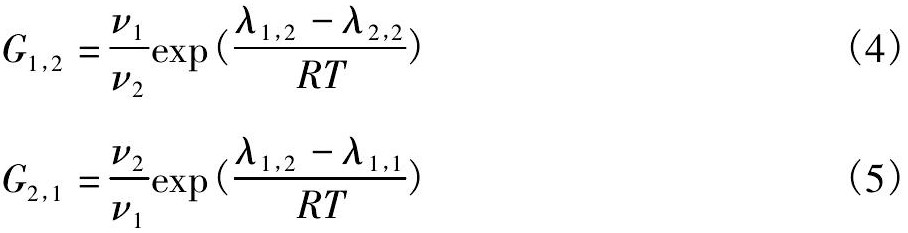
式中 ν₁, ν₂分别为Ti Cl₄和CH₂Cl₂的摩尔体积, λ_1，2- λ_2，2, λ_1，2- λ_1，1为Ti Cl₄-CH₂Cl₂二元系的相互作用参数, G_1，2和G_2，1为Ti Cl₄-CH₂Cl₂二元系的Wilson方程参数。

表1 Ti Cl₄-CH₂Cl₂二元系MOSCED模型参数Table 1 Parameters of MOSCED model for Ti Cl₄-CH₂Cl₂system  下载原图

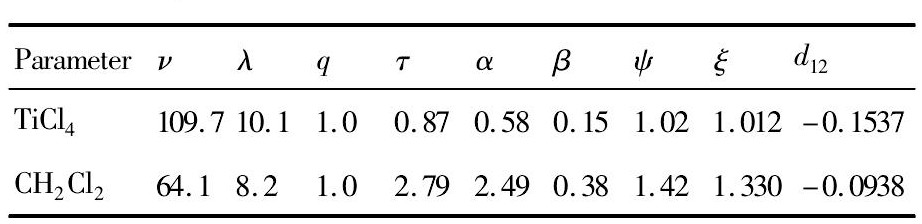
The parameter of Ti Cl₄being calculated according to method provided by Ref.[12], the parameter of CH₂Cl₂being cited from Refs.[12, 13]

表1 Ti Cl₄-CH₂Cl₂二元系MOSCED模型参数Table 1 Parameters of MOSCED model for Ti Cl₄-CH₂Cl₂system

表2 Ti Cl₄-CH₂Cl₂二元体系的无限稀释活度系数Table 2 Limiting activity coefficient for Ti Cl₄-CH₂Cl₂sys-tem  下载原图

表2 Ti Cl₄-CH₂Cl₂二元体系的无限稀释活度系数Table 2 Limiting activity coefficient for Ti Cl₄-CH₂Cl₂sys-tem

在无限稀释情况下:

将表2 中的数据代入式 ( 6) 和 ( 7) 求得Ti Cl₄-CH₂Cl₂二元系的和, 并由式 ( 4) 和 ( 5) 求得Ti Cl₄-CH₂Cl₂二元系的Wilson常数如表3 所示。

将表3 中的数据带入式 ( 2) 和 ( 3) , 可得到20 ℃ 下Ti Cl₄-CH₂Cl₂二元系的活度系数与组成之间的关系如图1 所示。由图1 可知, Ti Cl₄-CH₂Cl₂二元系中, Ti Cl₄的活度系数随混合物中Ti Cl₄的摩尔分数的增大而减小, CH₂Cl₂的活度系数随混合物中Ti Cl₄的摩尔分数的增大而增大。

2 Ti Cl4-CH2Cl2二元系的气液平衡

已知Ti Cl₄-CH₂Cl₂二元系的相互作用系数: λ_1，2- λ_2，2及 λ_1，2- λ_1，1 ( 其值在一定温度范围内为定值) , 可采用沸点或露点计算法计算Ti Cl₄-CH₂Cl₂二元系的气液平衡。在常压下, 气相的非理想性可忽略不计, 因此计算过程中气相视为理想状态。

表3 Ti Cl₄-CH₂Cl₂二元系的Wilson参数Table 3Parameters of Wilson equation for Ti Cl₄-CH₂Cl₂system  下载原图

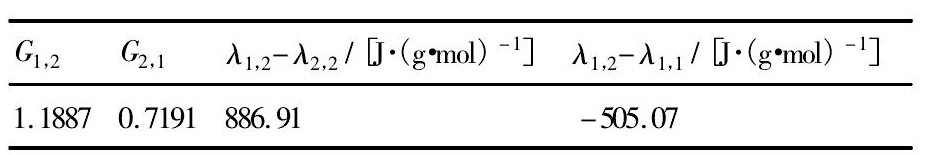
表3 Ti Cl₄-CH₂Cl₂二元系的Wilson参数Table 3Parameters of Wilson equation for Ti Cl₄-CH₂Cl₂system

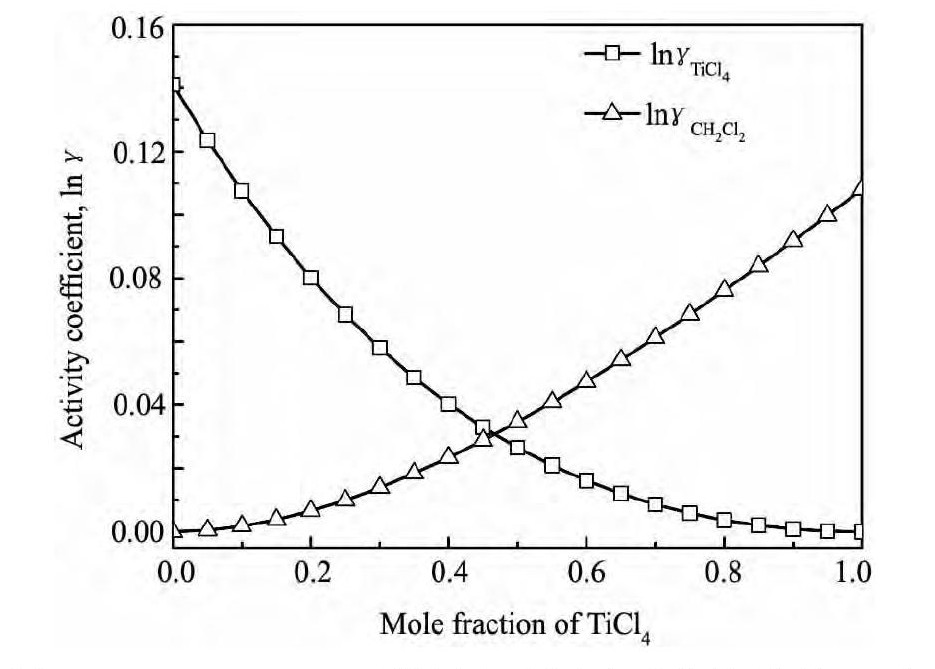
图1 Ti Cl4-CH2Cl2二元系的活度系数与组成的关系图 ( 20 ℃) Fig. 1 Plot of activity coefficient against composition for Ti Cl4-CH2Cl2system ( 20 ℃ )

2.1 Ti Cl4-CH2Cl2二元系的气液平衡计算

当二元系混合达到平衡时:

式中: x_i和y_i是液相和气相中组分i的摩尔分数, P为系统压力, P_i^S是纯液体i的蒸汽压, γ_i是液相组分i的活度系数。

而由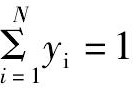 可得:

而对于Ti Cl₄-CH₂Cl₂二元系:

纯液体的蒸汽压采用Antoine方程计算:

式中P^S为纯液体的蒸汽压, A, B, C为纯液体的Antoine常数, 对于Ti Cl₄: A = 7. 683, B = 1964, C =0, 对于CH₂Cl₂: A = 7. 4092, B = 1325. 9, C = 20. 4。由此可得, Ti Cl₄, CH₂Cl₂蒸汽压于温度的关系:

Ti Cl₄和CH₂Cl₂的活度系数采用Wilson方程计算:式 (2) ~ (5) , 其中λ_{1, 2}-λ_{2, 2}=886.91 J· (g·mol) ^-1, λ_{1, 2}-λ_{1, 1}=-505.07 J· (g·mol) ^-1。

由此得到 γ₁, γ₂, P₁^S及P₂^S与温度的关系式, 根据图2 所示方框图采用试差法计算Ti Cl₄-CH₂Cl₂二元系的汽液平衡, 计算得到的数据如表4 所示。

表4 Ti Cl₄-CH₂Cl₂系的汽液平衡数据 ( 1 ×10⁵Pa) Table 4 VLE data for Ti Cl₄-CH₂Cl₂system ( 1 × 10⁵Pa)   下载原图

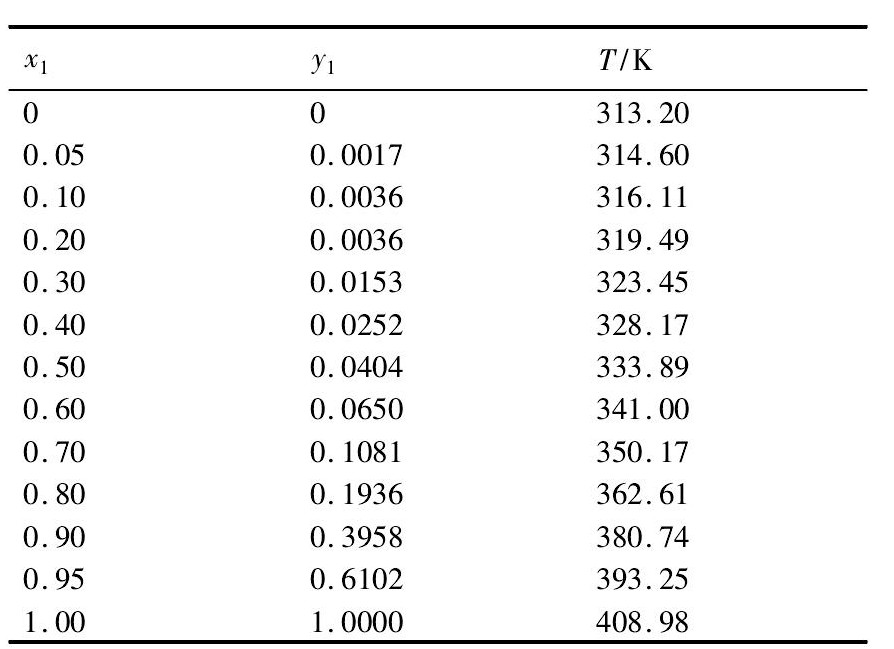
表4 Ti Cl₄-CH₂Cl₂系的汽液平衡数据 ( 1 ×10⁵Pa) Table 4 VLE data for Ti Cl₄-CH₂Cl₂system ( 1 × 10⁵Pa)

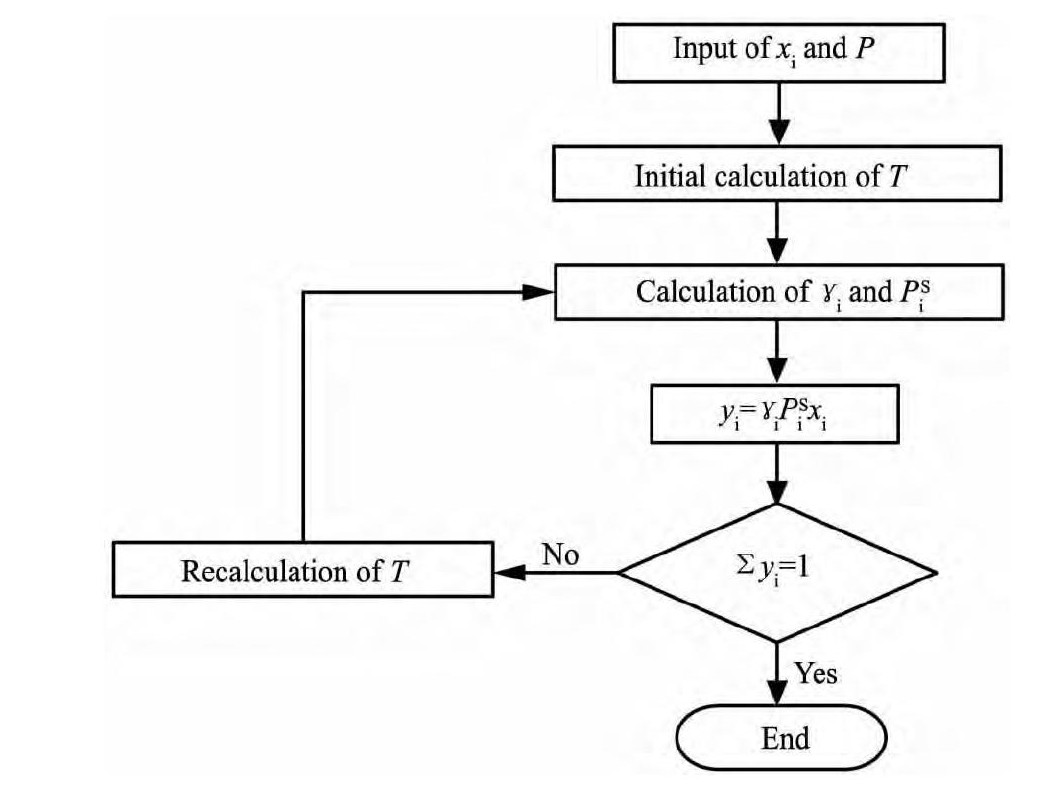
图 2 Ti Cl4-CH2Cl2二元系汽液平衡数据计算方框图Fig．2 Calculative block diagram for VLE data of Ti Cl4-CH2Cl2system

2. 2 Ti Cl4-CH2Cl2二元系的相图

根据Ti Cl₄-CH₂Cl₂二元系的汽液平衡数据, 以气相 ( y) 和液相 ( x) 中Ti Cl₄组成为横坐标, 温度为纵坐标作图得Ti Cl₄-CH₂Cl₂二元系的相图如图3所示; 以液相中Ti Cl₄组成 ( x) 为横坐标, 气相中Ti Cl₄组成 ( y) 为纵坐标作图得Ti Cl₄-CH₂Cl₂二元系的气液相组成图 ( y-x图) 如图4 所示。

3 结果与讨论

3. 1 误差分析

根据表4, 采用内插法计算得到Ti Cl₄-CH₂Cl₂混合物在323, 343, 363 及393 K平衡时残留液相中Ti Cl₄的摩尔分数, 其值如表5 中计算值所示;同时将Ti Cl₄与CH₂Cl₂混合物在323, 343, 363 及393 K下加热, 平衡后分析残留液相中Ti Cl₄的摩尔分数, 其值如表5 中实验值所示。由表5 可知, 计算得到的Ti Cl₄-CH₂Cl₂二元系汽液平衡数据与实验值比较, 误差为10% 左右, 可作为指导Ti Cl₄-CH₂Cl₂二元系蒸馏或精馏分离的理论依据。

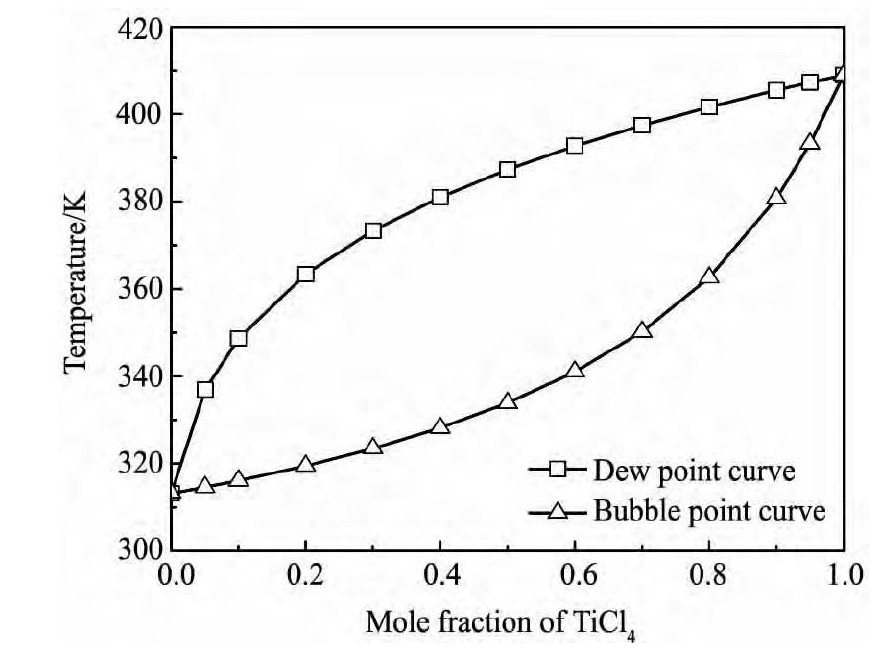
图3 Ti Cl4-CH2Cl2二元系的T-x-y相图 ( 1 × 105Pa) Fig. 3 T-x-y phase diagram for Ti Cl4-CH2Cl2system ( 1 ×105Pa)

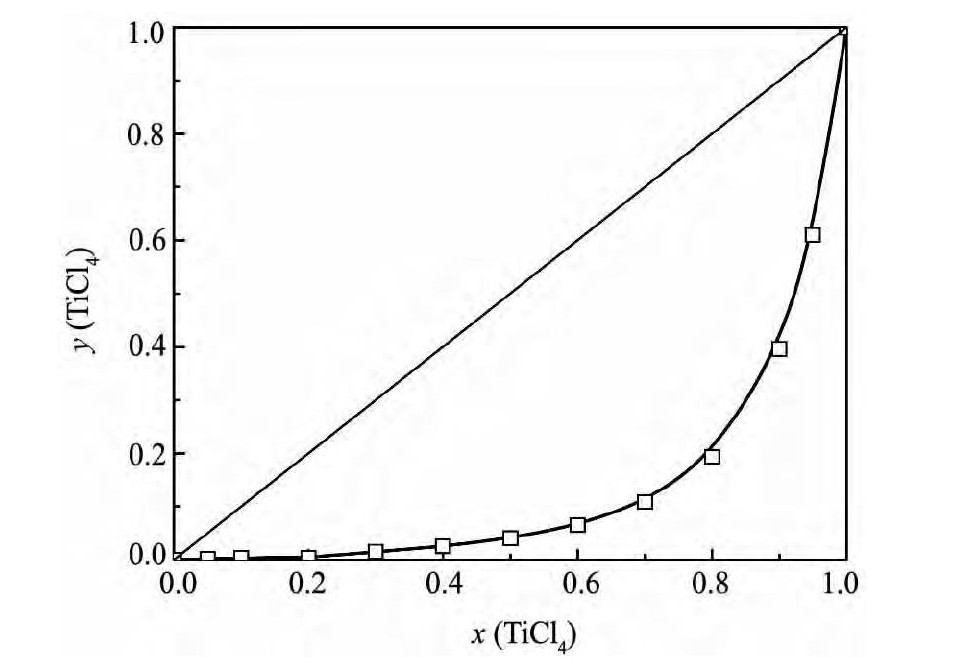
图 4 Ti Cl4-CH2Cl2二元系的 y-x 相图 ( 1 × 105Pa) Fig． 4 y-x phase diagram for Ti Cl4-CH2Cl2system ( 1 × 105Pa)

3. 2 Ti Cl4-CH2Cl2二元混合物性质分析

对于二元混合物的分离, 首先应判断其混合后是否形成共沸物和化合物, 如形成共沸物和化合物则不能通过简单蒸馏的方法将其分离。二元系是否形成共沸物可通过无限稀释活度系数确定^［12］。

如二元系活度系数满足下列关系式:

γ1∞<PP12SS<γ12∞或 γ1∞>PP21SS>γ12∞ ( 14)

则二元系在有限浓度范围内存在共沸组成。

Ti Cl₄-CH₂Cl₂二元系的及计算值如表6所示。

表5 Ti Cl₄-CH₂Cl₂系汽液平衡计算值与试验值对比Table 5 Comparison for calculated and experimental data of Ti Cl₄-CH₂Cl₂system  下载原图

表5 Ti Cl₄-CH₂Cl₂系汽液平衡计算值与试验值对比Table 5 Comparison for calculated and experimental data of Ti Cl₄-CH₂Cl₂system

表 6 Ti Cl4-CH2Cl2二元系 γ∞及PS2PS1的计算值Table 6 Calculated data of γ∞andPS2PS1for Ti Cl4-CH2Cl2system  下载原图

表 6 Ti Cl4-CH2Cl2二元系 γ∞及PS2PS1的计算值Table 6 Calculated data of γ∞andPS2PS1for Ti Cl4-CH2Cl2system

由表6 可知, Ti Cl₄-CH₂Cl₂二元系活度系数不满足式 ( 14) , 因此Ti Cl₄和CH₂Cl₂混合不形成共沸物, 这也可从图3 及4 中没有共沸点而得到验证。

图5 为纯CH₂Cl₂, Ti Cl₄及Ti Cl₄-CH₂Cl₂混合物的拉曼光谱图。由图5 可知, 在全部波长范围 ( 0~ 3500 cm^{－ 1}) 内, CH₂Cl₂有4 个基本振动峰, 分别对应于65 和2980 cm^{－ 1}处的CH₂振动峰以及285和705 cm^{－ 1}处的CCl₂振动峰^{［15 － 16］}, Ti Cl₄有2 个振动峰位于128 和395 cm^{－ 1}处^［17］。Ti Cl₄-CH₂Cl₂混合物有6 个基本振动峰, 分别对应于CH₂, CCl₂和Ti Cl₄振动峰, 没有新的振动峰出现。因此CH₂Cl₂和Ti Cl₄混合过程中没有新化合物生成, 只是简单的溶解。

3. 3 Ti Cl4-CH2Cl2二元系混合物精馏分离分析

由图3 及4 可知, 随温度升高, 平衡液相中Ti Cl₄浓度迅速升高, 但平衡汽相中Ti Cl₄浓度也相应提高; 当温度为362. 6 K时, 液相中Ti Cl₄摩尔分数为0. 8, 气相中Ti Cl₄摩尔分数达到0. 19。因此, 采用蒸馏的方法可以实现Ti Cl₄与CH₂Cl₂的初步分离, 但要实现地深度分离则需采用精馏的方法。

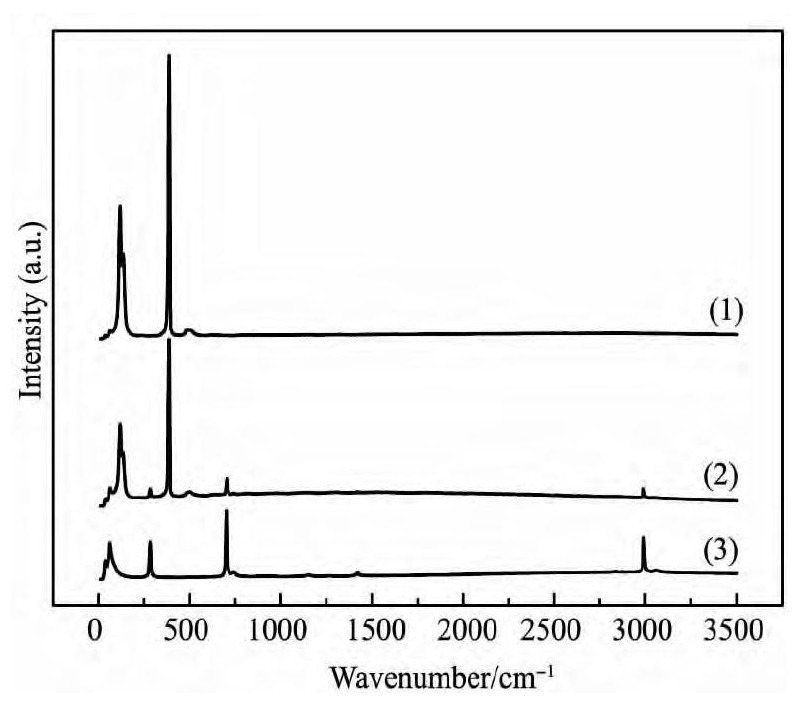
图5 Ti Cl4-CH2Cl2二元系的拉曼光谱Fig. 5 Raman spectra of Ti Cl4-CH2Cl2system

(1) Ti Cl₄; (2) Mixture of Ti Cl₄and CH₂Cl₂; (3) CH₂Cl₂

采用CH₂Cl₂回收沉淀泥桨中的Ti Cl₄, 得到的混合液中CH₂Cl₂含量为x_F= 0. 63 ( 摩尔分数) , 设定精馏塔顶馏出液CH₂Cl₂含量为x_D= 0. 97 ( 摩尔分数) , 釜液CH₂Cl₂含量为x_W= 0. 03 ( 摩尔分数) 。采用泡点进料, 回流比为0. 5, 采用图解法计算理论塔板数^［18］如图6 所示。由图6 可知, 在上述条件下实现Ti Cl₄与CH₂Cl₂的深度分离所需的塔板数为4。

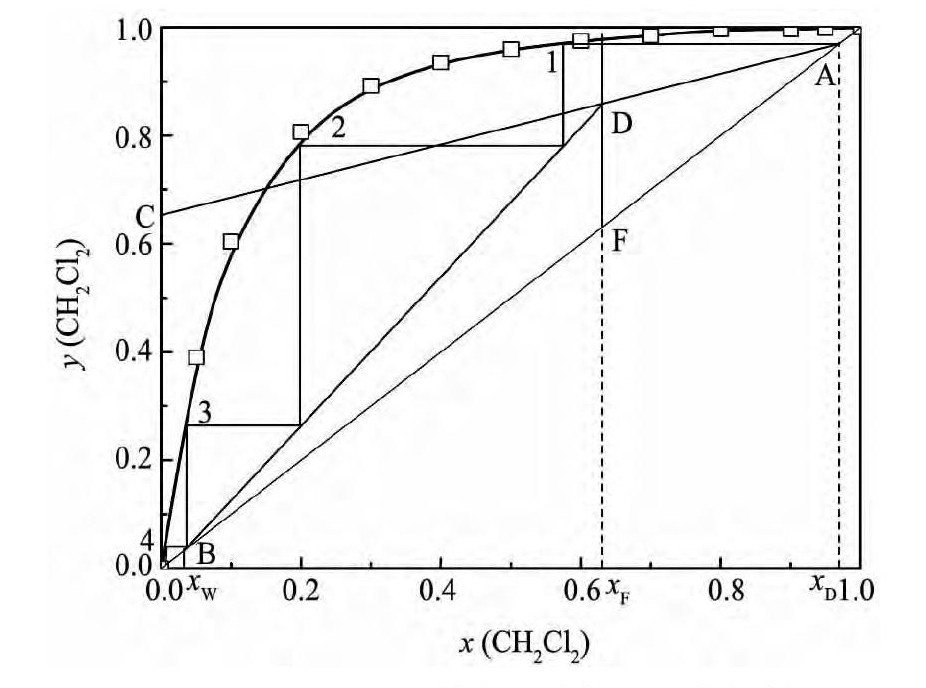
图6 CH2Cl2-Ti Cl4精馏分离的理论塔板数Fig. 6Theoretical trays of rectifying column for separation of CH2Cl2and Ti Cl4

4 结论

1. 用MOSCED模型计算了Ti Cl₄-CH₂Cl₂二元系的无限稀释活度系数, 20 ℃ 时Ti Cl₄和CH₂Cl₂的无限稀释活度系数分别为: 1. 151 和1. 114。并采用Wilson模型, 绘制了20℃ 时Ti Cl₄和CH₂Cl₂的活度系数图。

2. 拉曼光谱分析结果表明Ti Cl₄和CH₂Cl₂的混合过程中没有新化合物生成, 只是简单的溶解;同时Ti Cl₄和CH₂Cl₂混合不形成共沸物。

3. 计算得到了Ti Cl₄-CH₂Cl₂二元系的汽液平衡数据和汽液平衡图。结果表明, 通过蒸馏的方法可初步分离Ti Cl₄和CH₂Cl₂混合物, 但要实现地深度分离则需采用精馏的方法, 分离所需的塔板数为4。

参考文献

[1] Jin Z, Zhang W M.High temperature deformation behaviors of biomedical titanium alloy Ti-6Al-7Nb[J].Chinese Journal of Rare Metals, 2012, 36 (2) :218. (金哲, 张万明.生物医用Ti-6Al-7Nb合金高温变形行为研究[J].稀有金属, 2012, 36 (2) :218.)

[2] Shao Z K, Zhang W M, Huang Z G, Yuan Q H, Lei K.Superplastic forming and mechanical properties for TC4alloy negative-angle part[J].Chinese Journal of Rare Metals, 2012, 36 (4) :511. (邵宗科, 张文明, 黄重国, 袁清华, 雷鹍.TC4钛合金负角度零件超塑成型及性能研究[J].稀有金属, 2012, 36 (4) :511.)

[3] Wang X W, Tian J Q, Wang M Y, Guo R L, Peng J, Luo L.A drying treatment to dry precipitation slurry forming in raw titanium tetrachloride[P].Chinese Patent, CN102092783A, 2010. (王学文, 田建强, 王明玉, 郭荣林, 彭俊, 罗霖.一种四氯化钛沉淀泥浆干燥方法[P].中国专利, CN102092783A, 2010.)

[4] Wang X W, Xiang X Y, Wang M Y.A method of recovering titanium and niobium from slurry forming in raw titanium tetrachloride[P].Chinese Patent, CN102765749 A, 2012. (王学文, 向小艳, 王明玉.一种从粗四氯化钛沉淀泥浆中综合回收钛铌的方法[P].中国专利, CN102765749 A, 2012.)

[5] Deng G Z.The Metallurgy of Titanium[M].Beijing:Metallurgical Industry Press, 2010.318. (邓国珠.钛冶金[M].北京:冶金工业出版社, 2010.318.)

[6] Dean John A.Lange's Handbook of Chemistry[M].Shang J F, Cao S J, Xin W M, Zheng F Y, Lu X M, Lin C Q, et al translation.Beijing:Science Press, 1991.1699. (迪安J A.兰氏化学手册[M].尚久方, 操时杰, 辛无名, 郑飞勇, 陆晓明, 林长青等译.北京:科学出版社, 1991.1699.)

[7] Schreiber L B, Eckert C A.Use of infinite dilution activity coefficients with Wilson's equation[J].Ind.Eng.Chem.Process Des.Develop., 1971, 10 (4) :572.

[8] Fu J Q.Phase Equilibrium and Simulation Calculation of Distillation for Special System[M].Beijing:China Petrochemical Press, 2002.10. (傅吉全.特殊体系的相平衡和精馏模拟计算[M].北京:中国石化出版社, 2002.10.)

[9] Pierotti G J, Deal C H, Derr E L.Activity coefficients and molecular structure[J].Industrial and Engineering Chemistry, 1959, 51 (1) :95.

[10] Cheng Jaw-Shin, Tang Muoi, Chen Y P.Correlation and comparison of the infinite dilution activity coefficients in aqueous and organic mixtures from a modified excess Gibbs energy model[J].Fluid Phase Equilibria, 2004, 217 (2) :205.

[11] Hait Mitchell J, Liotta Charles L, Eckert Charles A.Space predictor for infinite dilution activity coefficients[J].Ind.Eng.Chem.Res., 1993, 32 (11) :2905.

[12] Thomas Eugene R, Eckert Charles A.Prediction of limiting activity coefficient by a modified separation of cohesive energy density model and UNIFAC[J].Ind.Eng.Chem.Process Des.Dev., 1984, 23 (2) :194.

[13] Lazzaroni Michael J, Bush David, Eckert Charles A.Revision of MOSCED parameters and extension to solid solubility calculations[J].Ind.Eng.Chem.Res., 2005, 44 (1) :4075.

[14] Fu L.Phase Equilibrium in Chemical Process Design[M].Beijing:Chemical Industry Press, 1985.42. (傅良.化工过程设计的相平衡[M].北京:化学工业出版社, 1985.42.)

[15] Hofmann M, Graener H.Time resolved incoherent anti-Stokes Raman spectroscopy of dichloromethane[J].Chemical Physics, 1996, 206 (1-2) :129.

[16] Edwards H G M, Farwell D W, Johnson A F.FT-Raman spectroscopic study of aluminium (III) chloride in acetonitrile and dichloromethane solutions containing water[J].Journal of Molecular Structure, 1995, 344 (1-2) :37.

[17] Chen R C.The research on the hydrolysis of titanium tetrachloride[J].Hydrometallurgy of China, 1999, 71 (3) :1. (陈瑞澄.四氯化钛水解过程研究[J].湿法冶金, 1999, 71 (3) :1.)

[18] Feng X, He C H.Principles of Chemical Industry[M].Beijing:Science Press, 2007.87. (冯霄, 何潮洪.化工原理[M].北京:科学出版社, 2007.87.)