堆石料湿化变形三轴试验研究
彭凯1, 2,朱俊高1, 2,王观琪3
(1. 河海大学 岩土力学与堤坝工程教育部重点实验室,江苏 南京,210098;
2. 河海大学 岩土工程研究所,江苏 南京,210098;
3. 成都勘测设计研究院 工程分院,四川 成都,610072)
摘 要:采用大型三轴仪分别进行各向等压及不同围压不同湿化应力水平条件下的三轴湿化试验,对堆石料在上述情况下的湿化变形特性进行研究。基于单线法,建立适合于堆石料湿化变形的新模型,通过研究湿化轴向变形及体积变形与围压以及湿化应力水平的关系,提出单线法湿化变形经验公式,并结合试验成果对堆石料的湿化模型参数进行拟合。研究结果表明:在各向等压条件下,湿化体积变形与轴向变形和围压的关系分别可用双曲线与直线表示;在围压一定时,偏应力引起的湿化体积变形与湿化应力水平的关系可采用线性拟合,而湿化轴向变形与湿化应力水平呈指数关系;拟合曲线与试验结果曲线较吻合,表明该模型能较好地反映堆石料湿化变形的特征,证实了该模型的合理性。
关键词:堆石料;湿化变形;单线法;湿化应力水平
中图分类号:TU41 文献标志码:A 文章编号:1672-7207(2010)05-1953-08
Study on slaking deformation of rockfill materials by triaxial test
PENG Kai1, 2, ZHU Jun-gao1, 2, WANG Guan-qi3
(1. Key Laboratory of Geo-mechanics and Embankment Engineering, Ministry of Education,
Hehai University, Nanjing 210098, China;
2. Geotechnical Research Institute, Hehai University, Nanjing 210098, China;
3. Engineering Branch of Chengdu Hydroelectric Investigation and Design Institute, Chengdu 610072, China)
Abstract: Large triaxial machine was used for the triaxial slaking tests under isotropic and different slaking stresses level with different confining pressures. The slaking deformation properties of the rockfill materials under the above mentioned conditions were analyzed. A new model that fits for the slaking deformation of rockfill was established based on the single-line method. The empirical formula of single-line method was established according to the analysis of slaking axial deformation and slaking volume deformation with slaking stress levels and confining pressures, and the model parameters were fitted from the test results. The results show that on the condition of isotropic, the relationship between slaking volume deformations and confining pressures can be expressed by hyperbolas, but the linear relation between the slaking axial deformation and confining pressures. For certain confining pressures, the slaking volume deformations which are caused by deviatoric stress are linear to the slaking stress levels, while the exponential relation between the slaking axial deformations and the slaking stress levels. The fitting value is identical with experimental curve and the properties of the rockfill materials are reflected well by the new model. So, the model is reasonable.
Key words: rockfill materials; slaking deformation; single-line method; slaking stress level
土石坝堆石料湿化变形指堆石料由干态遇水变成湿态时所产生的变形。在堆石坝建设和运行过程中,水库蓄水、水位上下波动、雨水浸入坝体等,都会使粗粒料浸水湿化产生变形。湿化变形是产生堆石坝后期变形的主要因素之一。近年来,国内外学者针对堆石料的湿化特性进行了大量的研究,取得了一定进展。目前,对于粗粒料湿化变形无论是试验还是有限元计算,主要有双线法和单线法2种思路。Nobari等[1]提出“双线法”,即分别进行土体干态和湿态的三轴剪切试验,从而求出某一应力状态下的变形差,该值即为湿化变形量;朱百里等[2]提出“单线法”,通过不同湿化应力水平和围压的实验来确定湿化变形量。上述研究成果分别从2个不同的角度对湿化变形进行研究,具有一定的理论和工程实用价值。但是,由于堆石料湿化特性的重要性、湿化机理的复杂性、湿化试验的难度较大等原因,目前,在高土石坝设计中,无论是粗粒料湿化变形的试验、理论,还是数值模拟,仍没有得到很好解决[3]。如“双线法”不能反映等压应力状态下的湿化变形,且有关资料显示其计算的湿化变形量偏小,偏小值对于工程而言是不安全的。“单线 法”由于能更接近土体的实际浸水湿化应力状态,得到的湿化变形更接近实际情况[4],但是,由于试验中误差难以避免,离散型较大,采用不同的研究手段,所得结论不一致,统一的规律性较差。对于湿化体积变形,沈珠江等[5]认为湿化体积变形在整个湿化变形过程中为常数;李全明等[6]根据试验结果,认为湿化引起的体应变与围压有关,从而对沈珠江湿化模型进行了改进;刘祖德[7]认为在某一围压下,湿化体积变形随应力水平的增大表现出先增后减的关系;左元明等[8]发现,在某一围压下,湿化体变随应力水平的增大而增大;李鹏等[9]的研究表明,湿化体变与应力水平呈反比例关系;王富强等[10]的试验结果表明,湿化引起的体应变不仅与围压有关,而且与剪应力(应力水平)有关;魏松等[11-12]认为湿化体积变形随应力水平变化的关系主要受粗粒料干密度的影响,随着粗粒料干密度的不断增大,湿化体变与应力水平的关系依次由一直增大向一直减小过度。而徐晗等[13-14]研究表明,湿化体变和应力水平的关系与干密度并没有明显的关系。显然,由于影响湿化变形的因素较多,如密实程度、细粒含量、材料特性等,上述各模型均无法准确、全面反映粗粒料的湿化变形特性,很难将各因素都考虑到湿化模型中。因此,在研究粗粒料湿化变形特性时,有必要依据试验结果及所研究的目标,建立吻合于试验和实际情况的模型。在此,本文作者根据堆石料的工程特点,通过大型三轴试验研究堆石料浸水湿化过程中湿化轴向变形与湿化体积变形在不同围压和湿化应力水平下的变形规律,分析堆石料湿化特性,探讨建立合理的“单线法”湿化模型,并基于三轴湿化变形试验成果,得出该模型参数的确定方法。
1 堆石料湿化试验成果及分析
1.1 试验材料、方案及方法
试验采用的堆石料为似斑状黑云母钾长花岗岩( ),岩石呈灰白色,由斑晶和基质2部分组成,似斑状结构,块状-片麻状构造,部分具有由斑晶定向排列组成的流线构造。
),岩石呈灰白色,由斑晶和基质2部分组成,似斑状结构,块状-片麻状构造,部分具有由斑晶定向排列组成的流线构造。
本次的试验在大型三轴仪上进行。试样直径为30 cm,高为60 cm。根据规范[15],试验最大粒径取6 cm,不均匀系数Cu=6.1,曲率系数Cc=1.2,制样干密度ρd=2.04 g/cm3,相对密度Dr=0.9。堆石料设计平均级配曲线及采用混合法进行缩尺后的试验级配曲线如图1所示。
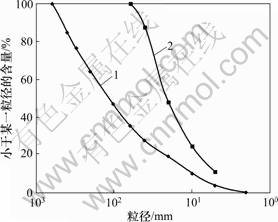
1—设计平均曲线;2—试验级配曲线
图1 堆石料级配曲线
Fig.1 Gradation curve of rockfill
为进行堆石料湿化变形研究,对各向等压及不同湿化应力水平的湿化变形进行试验。湿化应力水平是指试样由干态剪切到某一应力状态,然后进行浸水饱和湿化所对应的干态时的应力水平,用Sw表示。各向等压条件设计为0.5,0.8,1.2和1.8 MPa共4个围压;不同湿化应力水平试验分为3组,分别对应围压0.8,1.2和2.4 MPa,每个围压下从低到高共设计4个湿化应力水平。图2所示为试验方案示意图。其中:ε1为轴向变形;q为偏应力。
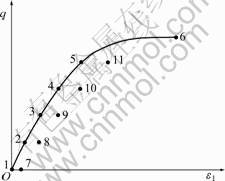
图2 试验方案示意图
Fig.2 Sketch map of test scheme
图2中,点1~5所表示的点代表某一围压下干态样试验结束时刻的应力-应变状态,点6代表干态样剪切峰值强度。点7~11分别表示在与对应点1~5处于相同的受力状态下进行浸水饱和湿化试验稳定后的应力-应变状态。通过以上试验,可以得到各向等压以及不同湿化应力水平的湿化变形量。
实验前,先将土样风干,称为“干态”,按图1所示的试验级配配料制样,分5层均匀振捣至控制干密度。试验时,在一定围压下等向固结直到稳定,当试样达到设计的固结压力或者剪切至预定的应力水平时,保持应力状态不变,进行浸水饱和。当浸水后的轴向变形以及体积变形达到稳定后视为湿化完成。
1.2 等压条件下湿化变形
1.2.1 湿化体积变形
各向等压(即湿化应力水平Sw=0)是最简单的应力状态,通过分析堆石料在不同围压下湿化体积变形,可绘出围压(σ3)与湿化体积变形(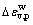 )的关系曲线,如图3所示。从图3可以看出:围压越大,湿化体积变形也越大。经过拟合可以发现,各向等压条件下湿化体变与围压之间满足以下关系:
)的关系曲线,如图3所示。从图3可以看出:围压越大,湿化体积变形也越大。经过拟合可以发现,各向等压条件下湿化体变与围压之间满足以下关系:
 (1)
(1)
其中:A0和B0为材料参数;pa=1.01×105 Pa。
1.2.2 湿化轴向变形
图4所示为不同围压下湿化轴向变形的变化关系。湿化轴变( )与围压基本上呈线性增长关系:
)与围压基本上呈线性增长关系:
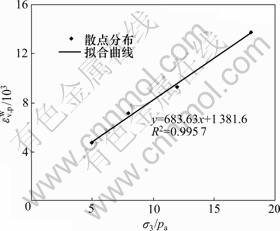
图3 各向等压湿化体变试验曲线
Fig.3 Experimental of slaking volume on condition of isotropy

图4 各向等压湿化轴变试验曲线
Fig.4 Experimental of slaking axial on condition of isotropy
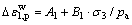 (2)
(2)
其中:A1和B1为材料参数;由图4可知,A1=0.004 5,B1=0.013 7。
1.2.3 等压湿化体变与轴变的关系
理论上,对于各向同性的材料,等压条件下湿化体变(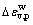 )与湿化轴变(
)与湿化轴变( )之比应该等于3,即
)之比应该等于3,即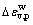 /
/ =3。试验结果测试的湿化体变与湿化轴变的比值并不等于3,而是在3附近,如图5所示。对于颗粒任意排列的重塑土样,这种离散性可能与材料性质、密实程度、围压、实验误差等因素有关,但基本上可以假定等压条件下湿化变形各向同性。
=3。试验结果测试的湿化体变与湿化轴变的比值并不等于3,而是在3附近,如图5所示。对于颗粒任意排列的重塑土样,这种离散性可能与材料性质、密实程度、围压、实验误差等因素有关,但基本上可以假定等压条件下湿化变形各向同性。
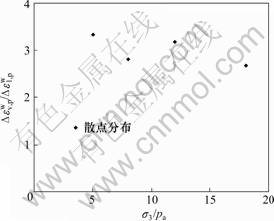
图5 各向等压湿化体变与轴变比关系曲线
Fig.5 Relationship curve of ratio of slaking volume to axial under isotropy
1.3 不同湿化应力水平下湿化变形
1.3.1 湿化轴向变形
图6所示为不同围压下,湿化轴向变形与应力水平(Sw)的关系。从图6可以发现:堆石料的湿化轴向应变与其所受的应力状态关系密切,且规律性强。某一围压下,应力水平越大,湿化轴向变形越大;当应力水平达0.6后,湿化轴向应变随应力水平的增加而急剧增加;当应力水平不大时,围压越大,其轴向应变也略大。
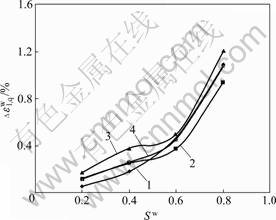
应力水平/MPa: 1—0.8; 2—1.2; 3—2.4; 4—平均值
图6 湿化应力水平表示的不同围压下湿化轴变曲线
Fig.6 Slaking axial curves indicated by slaking stress level under different confining pressures
经拟合,湿化轴向应变与应力水平及其围压可以表示为指数函数关系:
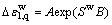 (3)
(3)
其中:Sw为湿化应力水平;A和B为与围压(σ3)有关的参数。
1.3.2 湿化体积变形
在偏应力条件下,堆石料湿化体积应变不仅与湿化时的应力水平有关,而且与湿化时的围压有关。在某一特定围压下,湿化体积应变随湿化应力水平呈线性增长。当应力水平相同时,湿化体积应变随围压增长而增长。图7所示为湿化体积应变与应力水平以及围压的关系,经拟合有以下关系:
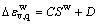 (4)
(4)
式中:Sw为湿化应力水平;C和D为与围压有关的参数。
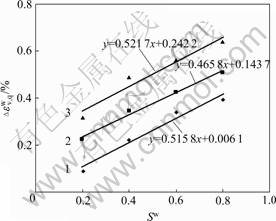
应力水平/MPa: 1—0.8; 2—1.2; 3—2.4
图7 湿化应力水平表示的不同围压下湿化体变曲线
Fig.7 Slaking volume curves indicated by slaking stress level under different confining pressure
1.3.3 湿化体变与轴变的关系
图8所示为在不同的应力水平和围压下湿化体变(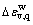 )与湿化轴变(
)与湿化轴变(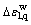 )的关系。从图8可以看出:
)的关系。从图8可以看出:
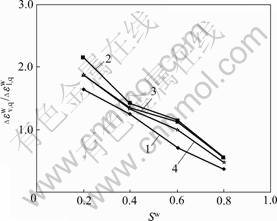
应力水平/MPa: 1—0.8; 2—1.2; 3—2.4; 4—平均值
图8 湿化应力水平表示的不同围压湿化体变与轴变曲线
Fig.8 Relationship curves between slaking volume deformation and slaking axial deformation indicated by stress level
某一围压下,随着应力水平的增大,湿化体变与湿化轴变的比值逐渐减小。这一点与等压条件湿化体变同湿化轴变的关系不同。
2 单线法模型的建立
2.1 模型建立的基本假定
为了建立粗粒料湿化模型,首先进行如下假定:(1) 湿化体变可分为由围压(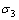 )引起的湿化体积变形(
)引起的湿化体积变形(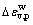 )与由偏压(
)与由偏压(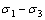 ,其中,
,其中, 为大主应力)引起的湿化体积变形(
为大主应力)引起的湿化体积变形(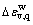 )之和;(2) 等压(即湿化应力水平Sw=0)条件下,湿化变形各向相等;(3) 当围压相等时,土体的剪切强度与其干湿状态无关。
)之和;(2) 等压(即湿化应力水平Sw=0)条件下,湿化变形各向相等;(3) 当围压相等时,土体的剪切强度与其干湿状态无关。
2.2 模型方程的建立
根据以上假定及魏松[16]的研究,认为湿化轴向变形与湿化体积变形都可视为分别由球应力和偏应力引起的变形之和,如式(5)和(6)所示。基于本文试验拟合资料,对魏松[16]所提出湿化轴向变形和湿化体积变形的拟合公式进行改进:球应力引起的湿化体积变形与围压的关系用双曲线表示;偏应力带来的湿化体积变形以及轴向变形与湿化应力水平的关系分别采用线性与指数关系进行拟合,使之与实际情况更加相符。单线法湿化变形数学模型公式可表示为:
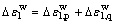 (5)
(5)
 (6)
(6)
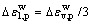 (7)
(7)
 (8)
(8)
 (9)
(9)
 (10)
(10)
其中:
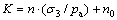 (11)
(11)
 (12)
(12)
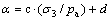 (13)
(13)
 (14)
(14)
下标“p”和“q” 分别表示各向等压(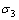 )和偏应力(
)和偏应力(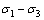 )作用的情况;pa=1.01×105 Pa;
)作用的情况;pa=1.01×105 Pa; 和
和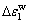 分别为湿化体变和湿化轴变;a, b, K, m,
分别为湿化体变和湿化轴变;a, b, K, m, 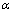 和
和 为模型参数;c, d, f, g, l, l0, n和n0为待定系数,由试验 确定。
为模型参数;c, d, f, g, l, l0, n和n0为待定系数,由试验 确定。
由式(5)~(14)得湿化剪应变为:
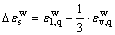 (15)
(15)
将式(9)~(10)代入(15)得:
 (16)
(16)
2.3 模型参数的确定
2.3.1 各向等压湿化体变参数a和b的确定
根据各向等压试验(Sw=0)的试验成果,按照式(1)拟合,由图3可以确定湿化体变参数a=1 381.60,b=683.63。
2.3.2 湿化轴变参数K和m的确定
由围压和偏应力引起的轴变分别为 及
及 ,据式(5)与(7)有:
,据式(5)与(7)有:
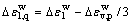 (17)
(17)
由式(9)和(11)得:
 (18)
(18)
根据图6,可以得到不同围压下的K,由式(11),用过原点的直线来拟合K与围压的关系,如图9所示,即可得到n和n0分别为0.004 1和0。经研究发现,K与m近似满足线性关系,如图10所示,由此可以得到:
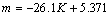 (19)
(19)
由 得:
得:
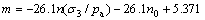 (20)
(20)
由式(12)有:
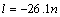 ,
,  (21)
(21)
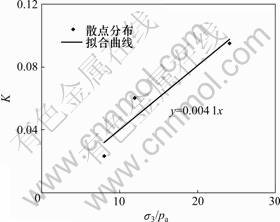
图9 参数K与σ3/pa关系曲线
Fig.9 Relationship between parameter K and confining pressure σ3/pa
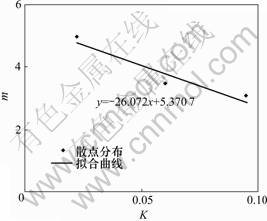
图10 参数K与m关系曲线
Fig.10 Relationship curve between parameters K and m
2.3.3 湿化体变参数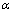 和
和 的确定
的确定
湿化体变分别由围压(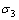 )和偏压(
)和偏压(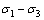 )引起,根据式(6)可以得到由偏应力引起的湿化体积变形
)引起,根据式(6)可以得到由偏应力引起的湿化体积变形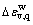 为:
为:
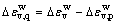 (22)
(22)
依据式(10),(13)~(14)得到:
 (23)
(23)
根据采用湿化应力水平表示的不同围压下湿化体变曲线,如图7所示,可得到一组 和
和 值。其中:pa为大气压力,引入pa使横坐标变为无因次量。
值。其中:pa为大气压力,引入pa使横坐标变为无因次量。 和
和 与围压的关系分别如图11和图12所示。由式(13)~(14)即可求出c, d, f和g分别为0.001 4,0.481 2,0.207 1,-0.403 7;由式(21)可知l和l0分别为-0.107,5.371。
与围压的关系分别如图11和图12所示。由式(13)~(14)即可求出c, d, f和g分别为0.001 4,0.481 2,0.207 1,-0.403 7;由式(21)可知l和l0分别为-0.107,5.371。
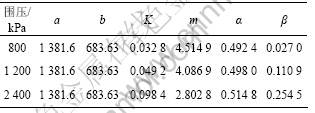
如上所述,模型参数如表1所示。
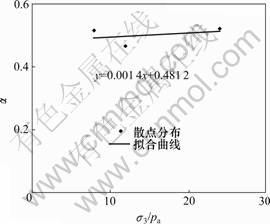
图11 参数α与σ3/pa关系曲线
Fig.11 Relationship curve between parameters α and σ3/pa
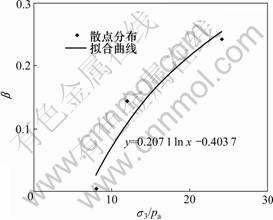
图12 参数β与σ3/pa关系曲线
Fig.12 Relationship between parameters β and σ3/pa
表1 模型拟合参数
Table 1 Fitting value of parameters of model
3 试验数据与计算结果对比分析
将表1中的参数代回前面建立的单线法湿化模型即可得到模型不同应力水平及不同围压湿化轴变和湿化体变的经验公式。图13所示为各向等压条件下实测和计算的湿化体变与围压的关系曲线,图14~15所示分别为偏应力条件下湿化轴变与体变随围压变化的实测值与计算值。
模型计算值与试验值误差分析分别如表2和表3所示。表2中, 。其中:
。其中: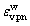 和
和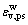 分别代表各向等压条件下模型拟合值与试验值。
分别代表各向等压条件下模型拟合值与试验值。
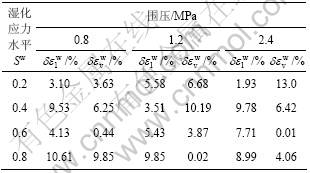
表3中,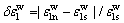 。其中:
。其中: 和
和 分别表示湿化轴向变形的拟合值与试验值;
分别表示湿化轴向变形的拟合值与试验值; ,
, 和
和 分别指湿化体积变形的拟合值与试验值。
分别指湿化体积变形的拟合值与试验值。
从图13~15可以看出:模型计算的湿化轴向变形和湿化体积变形与试验结果较吻合。结合表2和表3可知:在等压固结条件下,拟合值与试验值相对误差低于5%;在偏应力条件下,相对误差一般值都在10%以内;当湿化应力水平较高时(Sw≥0.8),湿化轴向变形相对误差为10%左右。
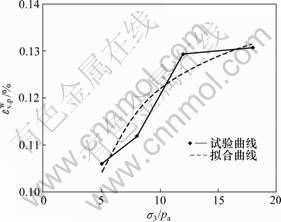
图13 试验与拟合的 与σ3/pa关系曲线
与σ3/pa关系曲线
Fig.13 Relationship curve between σ3/pa and  of test and fitting
of test and fitting
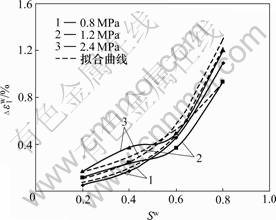
图14 试验与拟合的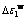 与Sw关系曲线
与Sw关系曲线
Fig.14 Relationship between  and Sw of test and
and Sw of test and
fitting value
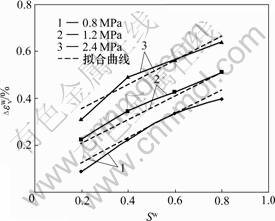
图15 试验与拟合的 与Sw关系曲线
与Sw关系曲线
Fig.15 Relationship between  and Sw of test and
and Sw of test and
fitting value
表2 等压条件下模型计算结果与试验值比较分析
Table 2 Comparison between simulation values and experimental results on condition of isotropic stress
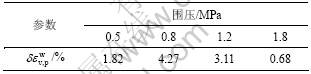
表3 偏应力条件下模型计算结果与试验值比较分析
Table 3 Comparison between simulation values and experimental results on condition of isotropic deviatoric stress
4 结论
(1) 湿化体积变形与围压呈双曲线关系,湿化轴向变形与围压可用直线关系表示,其两者的比值近似为常数。
(2) 湿化轴向应变主要与湿化时的应力水平有关,与小主应力关系不明显。对应于某一围压,堆石料湿化轴向应变与应力水平可采用指数函数表示。
(3) 堆石料湿化体积应变不仅与湿化应力水平有关,而且与围压也有关。当围压一定时,湿化体积应变与湿化应力水平呈线性关系;当应力水平一致时,围压越大,湿化体积应变也越大。
(4) 基于单线法建立的湿化变形模型能很好地反映堆石料湿化变形特征。模型与实验曲线拟合程度较好,表明了该模型的合理性及其工程实用性。
参考文献:
[1] Nobari E S, Duncan J M. Movement in dams due to reservoir filling[C]//Performance of Earth and Earth Supported Structures, Lafayette: ASCE, 1973: 797-815.
[2] 朱百里, 沈珠江. 计算土力学[M]. 上海: 上海科学技术出版社, 1990: 223-231.
ZHU Bai-li, SHEN Zhu-jiang. Calculation of soil mechanics[M]. Shanghai: Shanghai Science and Technology Press, 1990: 223-231.
[3] 沈珠江. 土石坝的本构模型和土质心墙坝蓄水变形数值模拟[R]. 南京: 南京水利水电科学研究院, 1989.
SHEN Zhu-jiang. Constitutive model of rockfill and numerical simulation of deformation of earth core dam after impounding water[R]. Nanjing: Nanjing Hydraulic Research Institute, 1989.
[4] 魏松, 朱俊高.粗粒土料湿化变形三轴试验研究[J]. 岩土力学, 2007, 28(8): 1609-1614.
WEI Song, ZHU Jun-gao. Study on wetting behavior of coarse grained soil in triaxial test[J]. Rock and Soil Mechanics, 2007, 28(8): 1609-1614.
[5] 沈珠江, 王剑平. 土质心墙坝填筑及蓄水变形的数值模拟[J]. 水利水运科学研究, 1988(4): 48-63.
SHEN Zhu-jiang, WANG Jian-ping. Numerical simulation of construction behavior of clay core dam and its movement due to reservoir impounding[J]. Hydro-Science and Engineering, 1988(4): 48-63.
[6] 李全明, 于玉贞, 张丙印, 等. 黄河公伯峡面板堆石坝三维湿化变形分析[J]. 水力发电学报, 2005, 24(3): 24-29.
LI Quan-ming, YU Yu-zhen, ZHANG Bing-yin, et al. Three dimensional analysis for the wetting deformation of Gongboxia concrete faced rock fill dam on the Yellow River[J]. Journal of Hydroelectric Engineering, 2005, 24(3): 24-29.
[7] 刘祖德. 土石坝变形计算的若干问题[J]. 岩土工程学报, 1983, 5(1): 1-13.
LIU Zu-de. Some problems about the calculation of deformation of earth-rock dams[J]. Chinese Journal of Geotechnical Engineering, 1983, 5(1): 1-13.
[8] 左元明, 沈珠江. 坝料土的浸水变形特性研究[R]. 南京水利科学研究院土工岩土所, 1989: 107-113.
ZUO Yuan-ming, SHEN Zhu-jiang. Study on the characteristics of the dam materials after impounding[R]. Nanjing: Nanjing Hydraulic Research Institute, 1989: 107-113.
[9] 李鹏, 李金, 刘金禹.粗粒料的大型高压三轴湿化试验研究[J]. 岩石力学与工程学报, 2004, 23(2): 231-234.
LI Peng, LI Jin, LIU Jin-yu. Slaking test study of coarse aggregate under high triaxial stress condition[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(2): 231-234.
[10] 王富强, 郑瑞华, 张嘎, 等. 积石峡面板堆石坝湿化变形分析[J]. 水利发电学报, 2009, 28(2): 56-60.
WANG Fu-qiang, ZHENG Rui-hua, ZHANG Ga, et al. Slaking deformation analysis for Jishixia concrete faced rockfill dam[J]. Journal of Hydroelectric Engineering, 2009, 28(2): 56-60.
[11] 魏松, 朱俊高, 王俊杰. 土石坝粗粒料湿化变形研究进展[C]//土石坝与岩土工程实践及探索. 北京: 中国电力出版社, 2004: 203-208.
WEI Song, ZHU Jun-gao, WANG Jun-jie. Development of study on wetting deformation of coarse-grained materials in earth dam[C]//Symposium on Application and Research of Earth Dam and Geotechnical Engineering. Beijing: China Electrical Power Press, 2004: 203-208.
[12] 魏松, 朱俊高. 粗粒料湿化变形三轴试验中的几个问题[J]. 水利水运工程学报, 2006(1): 19-23.
WEI Song, ZHU Jun-gao. Discussion on some problems in triaxial wetting test of coarse-grained materials[J]. Hydro-Science and Engineering, 2006(1): 19-23.
[13] 徐晗, 汪明元, 程展林, 等. 深厚覆盖层300 m超高土质心墙坝应力变形特征[J]. 岩土力学, 2008, 29(S1): 64-68.
XU Han, WANG Ming-yuan, CHENG Zhan-lin, et al. 3D stress and deformation characteristics of 300 m level high earth core dams with thick overburden layer[J]. Rock and Soil Mechanics, 2008, 29(S1): 64-68.
[14] 左永振, 程展林, 姜景山, 等. 粗粒料湿化变形后的抗剪强度分析[J]. 岩土力学, 2008, 29(S1): 559-562.
ZUO Yong-zhen, CHENG Zhan-lin, JIANG Jing-shan, et al. Analysis of shearing strength after wetting deformation of coarse-grained materials[J]. Rock and Soil Mechanics, 2008, 29(S1): 559-562.
[15] SL237–1999. 土工试验规程[S].
SL237–1999. Specification of soil test[S].
[16] 魏松. 粗粒料浸水湿化变形特性试验及其数值模拟研究[D]. 南京: 河海大学土木工程学院, 2006: 47-61.
WEI Song. Study on witting deformation behavior and numerical model of coarse-grained materials[D]. Nanjing: Hehai University. Civil Engineering Department, 2006: 47-61.
(编辑 刘华森)
收稿日期:2009-10-11;修回日期:2009-12-18
基金项目:水利部公益性行业科研专项基金资助项目(200801133);国家自然科学基金委员会、二滩水电开发有限责任公司雅砻江水电开发联合基金资助项目(50639050);中央高校基本科研业务费专项资金资助项目(2010B14814)
通信作者:彭凯(1981- ),男,湖南邵阳人,博士研究生,从事土体基本特性及本构关系研究;电话:15850588438;E-mail: pengkai@hhu.edu.cn