文章编号:1004-0609(2008)04-0710-07
Al-Cu合金凝固枝晶生长的数值模拟
占小红1,魏艳红1, 2,马 瑞1
(1. 哈尔滨工业大学 现代焊接生产技术国家重点实验室,哈尔滨 150001;
2. 南京航空航天大学 材料科学与技术学院,南京 210016)
摘 要:基于元胞自动机方法构建了枝晶生长数值模型,并将其应用于Al-Cu二元合金凝固过程的模拟。在该模型中,枝晶尖端生长速度模型基于溶质守恒建立。模拟过程中重点考虑不同冷却速率及形核条件对柱状树枝晶形态与溶质偏析的影响。计算结果表明,凝固过程中溶质易于富集在枝晶臂之间的封闭或半封闭区域。同时,随着冷却速率加大,晶界偏析变得更为显著。形核密度在一定程度上影响着枝晶形态,特别是影响着二次和三次枝晶的生长。
关键词:枝晶生长;数值模拟;元胞自动机
中图分类号:TG 111.4 文献标识码:A
Numerical simulation of dendritic grain growing during
Al-Cu alloy solidification
ZHAN Xiao-hong1, WEI Yan-hong1, 2, MA Rui1
(1. State Key Laboratory of Advanced Welding Production Technology, Harbin Institute of Technology,
Harbin 150001, China;
2. School of Materials Science and Technology, Nanjing University of Aeronautics & Astronautics,
Nanjing 210016, China)
Abstract: A dendrite grain growth model that is based on cellular automaton method was developed and applied to simulate the columnar dendrite grain growth during the directional solidification process of Al-Cu binary alloys. And the velocity model was based upon the solute conservation at the solid/liquid interface. The influences of different cooling speeds and different nucleation conditions on the dendrite morphologies and solute segregation were considered. The results indicate that the solute of high concentration liquids is easy to concentrate in the closed or semi-enclosed zones among secondary or tertiary dendrite arms. The grain boundary segregation becomes more severe when the cooling speed is increased. At the same time, the nucleation density affects the dendrite morphologies, especially the growth of secondary and tertiary dendrite arms.
Key words: dendrite growth; numerical simulation; cellular automaton
凝固过程中的枝晶生长,是一个复杂而重要的物理现象。实际工业生产过程中,金属或合金的凝固是一个不平衡的连续冷却过程,具有高温、动态等特点。因此,基于实验实时观察、检测凝固过程中的微观组织演变具有一定困难。随着计算机技术的日新月异和计算材料科学的迅速发展,宏观温度场及流场的计算已日趋成熟[1-2],模拟凝固过程中的微观组织演变已成为可能。对凝固过程微观组织进行数值计算与模拟,不仅有利于凝固理论研究的深入,而且对预测和控制微观组织和性能具有指导作用,在理论研究和工程应用上都具有深远意义。因此,近些年来,模拟凝固过程枝晶生长成为一个新的研究热点。
近20年以来,多种数值计算模型被应用于凝固过程枝晶生长的模拟。例如,ANDERSON等[3]和SPITLE等[4]运用Monte Carlo(MC)方法模拟了凝固过程晶粒生长[3-4]。其模拟结果在晶粒尺寸的计算、柱状晶到等轴晶转变的再现等方面取得了不菲的成果。GANDIN和RAPPAZ [5-6]使用Cellular Automata (CA,元胞自动机)方法,结合凝固过程传热的计算,对凝固过程枝晶生长进行了模拟。与此同时,相场方法也在凝固过程枝晶生长模拟中得以应用[7-8]。在上述各种方法中,CA法由于其具有物理基础明确、计算量可控等优点,目前在凝固过程枝晶生长的模拟中得到了广泛的应用。
元胞自动机应用于凝固过程组织模拟时,主要以凝固热力学、晶粒形核和生长动力学为依据,考虑了形核位置与生长取向的随机性。它克服了Monte Carlo方法物理基础不明确等缺点,并且能考虑过冷度和溶质扩散等多重因素的影响。WANG等[9]和DONG等[10]、BROWN[11-12]、GANDIN和RAPPAZ[5-6]、XU等 [13]、ZHU等[14]、LAN等[15]在该领域进行了卓有成效的工作,建立了元胞自动机与有限差分(CA-FD)、元胞自动机与有限单元法(CA-FE)的联合模型,并能基于三维非均匀温度场计算枝晶生长,取得了比较满意的结果。
关于柱状树枝晶的生长,部分研究局限于介观层次晶粒的模拟,而没有研究枝晶臂的生长[16-17];或者只研究了等轴晶的生长形态[18-19]。为此,本文作者基于CA方法进行Al-3%Cu合金定向凝固枝晶生长模拟的研究,在溶质守恒的基础上建立枝晶尖端生长速度模型。在设定的温度场的前提下,模拟计算一定形核条件下柱状树枝晶的生长,再现二次、三次枝晶生长,晶界偏析,以及不同晶粒之间的竞争生长等微观现象。
1 模型的建立
1.1 CA模型
二维体系中,一个元胞的形态通常可取为规则的正方形、正三角形或正六边形元胞。在正方形元胞体系中,对一个元胞的邻居关系结构最常用的有两种方式:
1) Von-Neumann 型邻居关系
它只考虑4个最近邻元胞,这种邻居关系也称为四邻居关系。
2) Moore 型邻居关系
它除了包括4个最近邻元胞,还考虑了对角位置的4个次近邻元胞, 因此周围共考虑8个邻居元胞,它也称为八邻居关系。
相应于Von-Neumann 型邻居关系的元胞自动机规则可描述为

演变规则的确定依赖于对系统宏观过程和真实物理机制的了解。本研究采用正方形元胞体系,Von-Neumann型邻居关系。
在基于元胞自动机计算凝固组织的研究中,目前KGT模型被广泛地应用在生长速度计算方面。KGT模型建立在“枝晶尖端拥有理想抛物线形状,以稳定的速度生长”等假设的基础上,并且动力学的过冷通常被忽略。这个模型对于一次枝晶的平均生长非常有说服力,但不能用于模拟非均匀间隔的枝晶尖端间的相互作用。同时,对于有复杂形式溶质场相互作用的二次枝晶臂和三次枝晶臂的生长情况,KGT模型也是无效的[9]。为此,本文作者基于枝晶尖端溶质扩散守恒,参考了NASTAC[20]关于枝晶尖端生长的模型,建立了Al-3%Cu合金凝固过程枝晶生长的速度模型。
1.2 枝晶生长速度模型
本研究基于枝晶尖端溶质守恒构建生长速度模型。如图1所示,将枝晶尖端简化为足够小的平面 时可以发现,在一个时间步?t内,由液相转变为固相 的体积为 ,其相应的溶质排放量 为:
,其相应的溶质排放量 为: 。
。
考虑 ,于是在x轴方向有如下的溶质守恒:
,于是在x轴方向有如下的溶质守恒:


图1 单元体生长示意图[21]
Fig.1 Sketch of growing in cell [21]
y轴方向的情况与此类似。于是,可以得到如下公式:

在考虑上述模型的通用性时,NASTAC[20]于1999年在上述公式中引入了固相分数,从而建立了一个统一的速度模型:

关于溶质扩散及生长速度模型的更多细节,请参考文献[20-21]。
1.3 边界条件和初始条件
本研究计算中采用周期性边界条件。参照DONG等的数据[10],对于Al-Cu二元合金,模拟所需各种初始参数的设定如表1所列。
表1 所使用的材料的性能和模拟参数[10]
Table 1 Material properties and model parameters used in simulations[10]
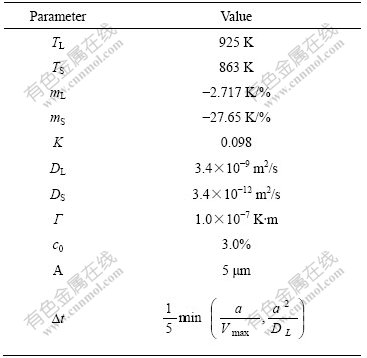
本研究的计算中,计算区域内的单元以相同的冷却速率冷却。凝固过程被假设为类定向凝固,在一定区域内以柱状枝晶的形态生长。
2 枝晶生长的数值模拟
在1 mm×1 mm的区域内,晶粒在该区域边缘形核并向过冷液体中生长。计算单元的尺寸为5 μm,即1 mm2的区域被剖分为200×200的网格。在计算过程中,对不同冷却速度和形核条件下Al-3%Cu合金凝固过程枝晶生长形态进行模拟。
2.1 柱状树枝晶生长
图2所示为等间距的5个晶核在200 K/s的冷却速率下不同时刻的生长形态。图2(a)~(d)所示分别为计算70 000、150 000、200 000、250 000 CAs(CAs为元胞自动机时间步)后的柱状枝晶形态。
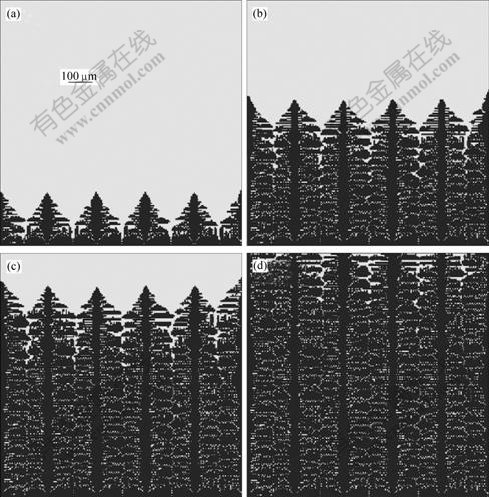
图2 不同时刻的柱状树枝晶形态
Fig.2 Morphologies of columnar grains at different times: (a) 70 000 CAs; (b) 150 000 CAs; (c) 200 000 CAs; (d) 250 000 CAs
对于Al-3%Cu合金体系,生长过程的原子堆积以粗糙界面(非小平面界面)的方式进行。凝固过程中,由于成分过冷的效应导致晶粒以柱状枝晶的形态生长。铝为面心立方结构,通常情况下,枝晶的各次晶轴均沿<100>晶向族的方向长大,且相互垂直。
在生长初始阶段,柱状枝晶各自快速地向过冷熔体中生长,如图2(a)所示。由于温度下降很快,每个柱状枝晶的生长速率非常接近,柱状枝晶之间的竞争生长并不明显。在柱状枝晶之间,由于一次枝晶表面的不稳定,已有明显的二次枝晶出现。150 000 CAs的柱状晶形态如图2(b)所示,此时的枝晶生长已经开始趋于稳定,一次轴方向上的竞争生长已经难以出现。
当柱状树枝晶生长至如图2(c)所示时,虽然各个一次枝晶轴的生长高度有所不同,但差距很小。计算时间步为250 000 CAs时,柱状晶形态如图2(d)所示。此时,凝固趋于结束,但仍然有少量液相残留于枝晶之间。经过之前各枝晶臂之间激烈的竞争生长,形成错综复杂的二次、三次枝晶形态。
图3所示为图2所对应的时刻下的溶质浓度分布。由图中可见,随着凝固的进行,溶质堆积加剧。同时,由于冷却速度较大,溶质来不及扩散,导致高浓度溶质堆积显著。在凝固趋于结束时,如图3(d)所示,枝晶间的溶质浓度最高达到14.54%,是初始浓度的4倍多。同时,由图3中可见,高浓度区域除了主要出现在枝晶前沿的液相中以外,在已凝固区域的残留液相区也存在。这是因为,凝固过程中,二次、三次枝晶的包围形成了一些封闭的区域,该区域里的残留液相难以与其他区域里的液相有效地进行溶质扩散。因此,随着凝固的继续进行,该区域内的液相中的溶质浓度不断增高。

图3 不同时刻的溶质浓度分布
Fig.3 Solute distributions at different times: (a) 70 000 CAs; (b) 150 000 CAs; (c) 200 000 CAs; (d) 250 000 CAs
2.2 不同形核条件与冷却速率的影响
图4和图5所示分别为模拟得到的250 K/s的冷却速率下不同时刻的柱状枝晶生长结果。图4(a)~(c)所示分别为70 000、120 000和200 000 CAs时刻的 柱状枝晶生长形态。图5(a)~(d)所示分别为70 000、120 000、180 000和225 000 CAs时刻的生长结果及溶质浓度分布。

图4 不同时刻的柱状树枝晶形态
Fig.4 Morphologies of columnar grains at different times: (a) 50 000 CAs; (b) 75 000 CAs; (c) 100 000 Cas
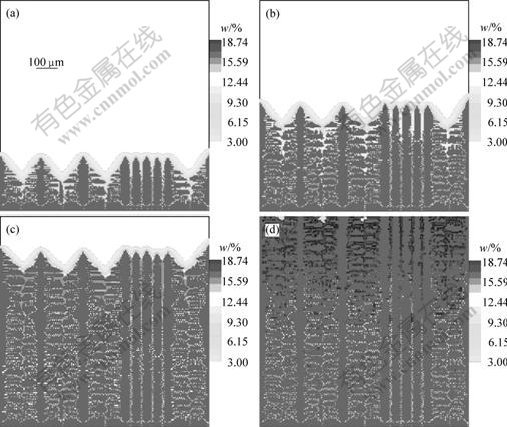
图5 不同时刻的溶质浓度分布
Fig.5 Solute distributions at different times: (a) 70 000 CAs; (b) 120 000 CAs; (c) 180 000 CAs; (d) 225 000 CAs
为了考虑不同形核条件的影响,在图4中,8个晶粒以非均匀间隔在计算区域边缘形核。由图中可见,计算区域右侧的形核密集区中主要呈现出柱状晶的生长形态。在该区域也存在少量的枝晶,但是其二次枝晶臂短小而稀少。然而,在计算区域左侧的形核非密集区中呈现出柱状枝晶的形态,二次枝晶臂生长充分。在不同区域中,一次枝晶轴因为竞争生长而被合并的情况并未出现。因此,在生长过程中,在其他条件不变的情况下,形核密度影响着枝晶的生长形态。这与先前研究的结果不完相符[10]。其主要原因可能是本研究模拟中所使用的冷却速率以及Al-3%Cu合金的物性参数决定的。
更快的冷却速率显然可获得更大的生长速度。图4中对应的冷却速率为250 K/s,而图3中对应的冷却速度是200 K/s。因此,同样是在200 000 CAs时刻,图4(c)中一次枝晶轴的长度明显大于图3(c)中的一次枝晶轴的长度。
同时,更快的冷却速率也带来了更严重的溶质偏析。在图5中,至凝固趋于结束的225 000 CAs时刻,枝晶尖端残留液相中的最大溶质浓度达到18.74%。而在图3(d)中,在冷却速率为200 K/s的条件下,到 250 000 CAs时刻,液相中最大溶质浓度仅为14.54%。另一个明显的现象是,从图5中可以看到,枝晶尖端区域液相中的溶质浓度明显高于枝晶根部区域液相中的溶质浓度,即先凝固的枝晶间的残留液相中的溶质浓度明显低于后凝固的枝晶间的残留液相中的溶质浓度。
图5所示清楚地再现了凝固过程溶质扩散。随着凝固的进行,新结晶出的固相不断向液相中排出溶质,枝晶尖端及枝晶之间的液相中溶质浓度不断增加。至120 000 CAs 时刻,液相中的溶质浓度已经达到11.5左右,如图5(b)所示。溶质富集主要是由以下因素造成。首先,由于生长速度大,溶质浓度高的液相来不及扩散,即没有充足的用于扩散的时间;其次,由于用于扩散的空间有限,特别是在被二次、三次枝晶包围形成的一些封闭或半封闭区域,高浓度区域难以与其他液相区形成具有浓度梯度的连续液相区域,扩散难以进行。同时,液相向固相中的反扩散的效果在该有限时间内是极其有限的。因此,随着凝固的进行,溶质富集不断加剧。
3 结论
1) 建立了基于元胞自动机的枝晶生长速度模型,基于该模型模拟了Al-Cu二元合金定向凝固过程中枝晶生长与溶质偏析等微观现象。
2) 计算结果表明,随着冷却速度增大,生长速度增加。同时,在其他条件不变的情况下,形核数量直接影响结晶形态。形核密集区容易形成柱状晶,而形核非密集区容易形成柱状树枝晶的形态。
3) 溶质扩散的计算结果显示,溶质偏析严重,高浓度区域往往集中于后期结晶的枝晶之间或被二次、三次枝晶包围形成的一些封闭或半封闭区域内。
4) 用元胞自动机方法进行Al-Cu合金凝固过程中枝晶生长的数值模拟,不仅可以再现其凝固过程中微观组织演变过程,同时还能进行枝晶间距、溶质偏析等方面的定量研究。
REFERENCES
[1] LIU Bai-cheng, XU Qing-yan. Advances on microstructure modeling of solidification process of shape casting[J]. Tsinghua Science and Technology, 2004, 9(5): 497-505.
[2] DONG Zhi-bo, WEI Yan-hong. Three dimensional numerical simulation of welding temperature fields in stainless steel[J]. China Welding, 2004, 13(1): 11-16.
[3] ANDERSON M P, SROLOVITZ D J, GREST G S. Computer simulation of grain growth—Ⅰ. Kinetics[J]. Acta Metall, 1984, 32(5): 783-791.
[4] SPITLE J A, BROWN S G R. Computer simulation of the effect of alloy variable on the grain structures of castings[J]. Acta Metal, 1989, 37(7): 1803-1810.
[5] GANDIN C A, RAPPAZ M. A coupled finite element- cellular automaton model for the prediction of dendritic grain structures in solidification processes[J]. Acta Metall, 1994, 42(7): 2233-2246.
[6] RAPPAZ M, GANDIN C A, TINTILLIER R. Three- dimensional simulation of the grain formation in investment casting[J]. Metallurgical Trans, 1994, 25(3): 629-635.
[7] QIN R S, WALLACH E R, THOMASON R C. A phase-field model for the solidification of multicomponent and multiphase alloys[J]. Journal of Crystal Growth, 2005, 279: 163-169.
[8] SUWA Y, SAUTO Y, ONODERA H. Three-dimensional phase field simulation of the effect of anisotropy in grain-boundary mobility on growth kinetics and morphology of grain structure[J]. Computational Materials Science, 2007, 40: 40-50.
[9] WANG W, LEE P D, MCLEAN M. A model of solidification microstructures in nickel-based superalloys: predicting primary dendrite spacing selection[J]. Acta Mater, 2003, 51: 2971-2987.
[10] DONG H B, LEE P D. Simulation of the columnar-to-equiaxed transition in directionally solidified Al-Cu alloys[J]. Acta Materialia, 2005, 53: 659-668.
[11] BROWN S G R. A 3-dimensional cellular automaton model of ‘free’ dendritic growth[J]. Scripta Metallurgica et Materialia, 1995, 32(2): 241-246.
[12] BROWN S G R. Simulation of diffusional composite growth using the cellular automaton finite difference (CAFD) method[J]. Journal of Materials Science, 1998, 33(19): 4769-4773.
[13] XU Q Y, LIU B C. Modeling of cast microstructure of Al alloy with a modified cellular automaton method[J]. Mater Trans, 2001, 42(11): 2316-2321.
[14] ZHU M F, LEE S Y, HONG C P. Modified cellular automaton model for the prediction of dendritic growth with melt convection[J]. Phys Rev E, 2004, 69(061610): 1-12
[15] LAN Y J, LI D Z, LI Y Y. Modeling austenite decomposition into ferrite at different cooling rate in low-carbon steel with cellular automaton method[J]. Acta Materialia, 2004, 52: 1721-1729.
[16] VANDYOUSSEFI M, GREER A L. Application of cellular automaton-finite element model to the grain refinement of directionally solidified Al-4.15wt%Mg alloys[J]. Acta Materialia, 2002, 50: 1693-1705.
[17] 刘永刚, 陈 军, 潘 冶, 孙国雄, 仇春荔. Al-4.5%Cu合金凝固过程显微组织的数值模拟[J]. 中国有色金属学报, 2002, 12(6): 1130-1135.
LIU Yong-gang, CHEN Jun, PAN Ye, SUN Guo-xiong, QIU Chun-li. Microstructure simulation of solidification process of Al-4.5%Cu binary alloy[J]. The Chinese Journal of Nonferrous Metal, 2002, 12(6): 1130-1135.
[18] 许 林, 郭洪民, 杨湘杰. 元胞自动机法模拟铝合金三维枝晶生长[J]. 铸造, 2005, 54(6): 575-578.
XU Lin, GUO Hong-min, YANG Xiang-jie. Simulating the three-dimensional dendritic growth of Al alloy using the cellular automata method[J]. Foundry, 2005, 54(6): 575-578.
[19] 丁恒敏, 刘瑞祥, 陈立亮, 刘晶峰. 用Cellular automaton模型方法模拟二元合金枝晶生长[J]. 中国铸造装备与技术, 2005, 2: 17-19.
DING Heng-min, LIU Rui-xiang, CHEN Li-liang, LIU Jing-fen. Simulation of treeing in binary alloy with cellular automaton[J]. China Foundry Machinery & Technology, 2005, 2: 17-19.
[20] NASTAC L. Numerical modeling of solidification morphologies and segregation patterns in cast dendritic alloys[J]. Acta Mater, 1999, 47(17): 4253-4262.
[21] WEI Y H, ZHAN X H, DONG Z B, YU L. Numerical simulation of columnar dendritic grain growth during weld solidification process[J]. Science and Technology of Welding and Joining, 2007, 12(2): 138-146.
基金项目:国家自然科学基金资助项目(50775112)
收稿日期:2007-07-30;修订日期:2007-12-02
通讯作者:占小红,博士研究生;电话:0451-86417650;E-mail: xhz_hit@yahoo.com.cn
(编辑 何学锋)