文章编号：1004-0609(2013)11-3031-08

薄壁铝合金压铸充型过程中铸件与铸型界面的换热行为

朱必武^{1, 2}，李落星^{1, 2}，刘  筱^{1, 2}，张立强^{1, 3}，徐  戎^{1, 2}，卜晓兵^{1, 2}

(1. 湖南大学 汽车车身先进设计与制造国家重点实验室，长沙 410082；

2. 湖南大学 机械与运载工程学院，长沙 410082；

3. 中南林业科技大学 机电工程学院，长沙 410004)

摘  要：采用压铸制备薄壁AlSi10MnMg铝合金铸件，用高速摄像技术记录分析压铸压射冲头的运动规律，并通过热平衡方程求解充型过程中铸件熔体和铸型之间的换热系数，最后通过数值模拟的方法讨论采用不同换热系数对充型仿真结果的影响。结果表明：充型流动长度随浇注温度的升高而增长；当充型处于液相线温度之上时，充型时间、换热系数随浇注温度的升高而增长；当充型至温度处于液相线温度以下时，充型时间和换热系数变化都很小。模拟仿真结果显示，采用基于热平衡方程求得的换热系数的计算模拟仿真结果与实验结果较一致。

关键字：薄壁铝合金；压铸；充型；换热系数；模拟仿真

中图分类号：TG249.2           　   　     文献标志码：A

Heat transfer behaviors between metal and die during filling process of thin-wall aluminum alloy under high pressure die casting conditions

ZHU Bi-wu^{1, 2}, LI Luo-xing^{1, 2}, LIU Xiao^{1, 2}, ZHANG Li-qiang^{1, 3}, XU Rong^{1, 2}, BU Xiao-bing^{1, 2}

(1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China;

2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China;

3. College of Mechanical and Electrical Engineering, Central South University of Forestry and Technology, Changsha 410004, China)

Abstract: The thin-wall AlSi10MnMg aluminum alloy samples were prepared by high pressure die casting. The motion laws of press-shoot ram were recorded by a high speed camera system and the heat transfer coefficients between the casting and mold were calculated by the energy conservation equation. Therefore, the effects of different heat transfer coefficients on the simulated filling results were discussed. The results show that the filling fluidity length increases with the pouring temperature increasing; when the filling process is above the liquidus, the filling time and the heat transfer coefficient increase with the pouring temperature increasing. However, when the filling process is below the liquidus, the changes of the filling time and the heat transfer coefficient are insignificant. The simulations using the heat transfer coefficient which is calculated by the energy conservation equation are well consistent with the experimental results.

Key words: thin-wall aluminum alloy; high pressure die casting; filling process; heat transfer coefficient; simulation

薄壁铝合金铸件具有质量小、力学性能优良等特点，近年来广泛应用于汽车车身和底盘等结构件，这类零件尺寸大且精度要求高、壁厚薄且结构复杂，其充型问题成为此类零件成形的关键问题^[1-2]。压铸作为一种快速的近净成型工艺，具有生产效率高、尺寸精度高和力学性能优异等特点，特别适合于此类零件的生产^[3]。同时，随着计算机技术的发展，针对压铸充型、凝固过程的数值模拟技术迅速发展起来，由于其可以预测铸件铸造缺陷的形成、数量以及分布位置，从而对优化此类零件成形的工艺提供参考^[4-5]。为了实现精确的数值模拟，准确的边界条件必不可少，其中界面换热系数被认为是一个最重要但又最难以测量和计算的参数^[6-7]。近年来，国内外对于确定铸件-铸型界面换热系数做了大量工作，在压铸领域也有少数相关报道^[8-9]，这些研究的共同特点是采用热电偶传感器记录采集铸件或者铸型的温度，然后通过反分析等方法求解得到铸件-铸型界面换热系数随时间或温度的变化关系^[7-8]。而以薄壁铝合金压铸件为研究对象时，其充型、凝固时间很短，如果也采用上述方法，由于热电偶传感器对于温度都有响应时间^[10]，其采集记录的温度数据还没来得及响应，薄壁铝合金压铸充型、凝固过程就已经完成，也就无法准确得到其充型、凝固过程中铸件-铸型界面换热系数。因此，本文作者以实际薄壁铝合金压铸实验为基础，通过高速摄像技术记录压射冲头的运动规律从而得到铝合金熔体充型、凝固过程中的动态流动过程，然后采用热平衡方程计算此过程中的换热系数，最后讨论采用此方法求得的换热系数对仿真结果的影响。

1  实验

1.1  合金熔炼

实验材料选用自配制的AlSi10MnMg铝合金，其配比成分(质量分数)为：10%Si，0.6%Mn，0.4%Mg，0.2%Ti，0.02%Sr，其余为Al。通过热力学计算分析和实验测得其液、固相线温度分别为897K 和825K。熔炼采用井式电阻石墨坩埚炉，C₂Cl₆精炼除气，Al-5Ti-B细化，Al-10%Sr变质，然后将合金液静置，准备实验。

1.2  试样制备

实验所用设备为江苏灌南125T压铸机，采用二级压射速度，调节设定慢压射速度为300 mm/s，快压射速度为4 000 mm/s，由慢转快时间为0.6 s，压射冲头直径60 mm，压射比压20 MPa，无设置增压，模具材料H13钢，模具试压5~6模预热至355~423 K，涂料为压铸用脱模剂，浇注温度分别为923、953、983和1 013 K。

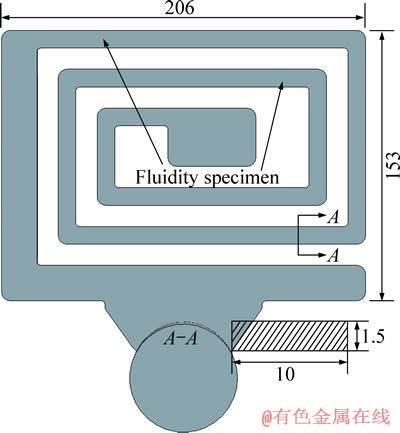
图1  流动试样尺寸图

Fig. 1  Drawing of fluidity specimen (Unit: mm)

图2  临界长度、极限长度定义示意图

Fig. 2  Schematic diagram of critical length and limiting length

压铸制得的薄壁AlSi10MnMg铝合金试样尺寸如图1所示，流动试样(Fluidity specimen)壁厚1.5 mm，宽10 mm，总长940 mm。如图2所示，定义压铸充型流动产生的第一个明显铸造缺陷的长度为临界长度(Critical length：L_fc)，总的充型长度为极限长度(Limiting length：L_fl)，分别测量记录其临界长度(L_fc)、极限长度(L_fl)。

1.3  冲头运动轨迹记录

如图3所示，在压射冲头活塞安装一运动参照物，此参照物与压射冲头始终保持相对静止，参照物运动轨迹由REDLAKE HG-LE高清摄像机记录，记录频率为1 000 Hz。通过摄像图像帧数描点得出压射冲头位移—时间曲线，对位移—时间曲线求导得出压射冲头速度曲线，充型过程各时刻节点直接从实验曲线中读取。

图3  冲头运动参照示意图

Fig. 3  Reference object of plunger

2  数学模型

金属熔体在过热情况下充填铸型，与铸型之间发生着强烈的热交换，是一个不稳定的换热过程，因此，液态金属对铸型的充填也是一个不稳定的动态流动过程。由于影响此过程的因素很多，从理论上对液态金属的充型能力进行计算很困难。因此假设：1) 熔体在整个过程中体积不可压缩、密度不变；2) 铸型与液态金属接触表面的温度在浇铸过程中不变；3) 液流断面上各点温度均匀；4) 热量仅按垂直于铸型的方向传导；5) 压铸充型过程中换热系数保持不变。

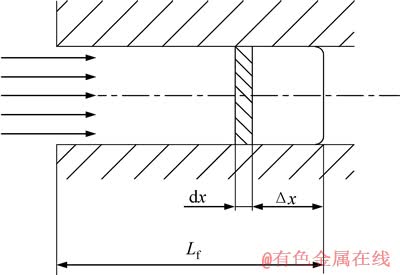
图4  充型过程示意图

Fig. 4  Schematic diagram of filling process

图2所示实验薄壁铝合金试样截面为矩形，充型过程示意图见图4^[11]，其充型流动长度可以分为两个阶段：1) 金属熔体温度降至液相线温度T_L时的充型长度；2) 金属熔体温度降至液相线温度T_L以下流动停止时的温度T_k时的充型长度。根据能量守恒定律分别列出其热平衡方程。

第一阶段(充型时间为τ₁)距液流端部Δx的dx元段，在dτ时间内通过散热面积dS散出的热量等于该时间内金属熔体温度下降dT放出的热量，其热平衡方式为

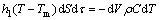                   (1)

式中：h₁为此阶段换热系数；T为金属熔体温度；T_m为铸型温度；dV为dx元段的体积；ρ为金属熔体的密度；C为熔体的热容。

其中：

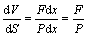                              (2)

式中：F为流动试样截面断面面积；P为流动试样截面断面周长。

故式(1)可写成

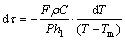                        (3)

代入边界条件τ=0时，T=T_j；τ=τ₁时，T=T_L；将式(3)积分后得

                         (4)

式中：T_j为浇注温度。

由式(4)有

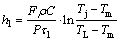                         (5)

第二阶段(充型时间为τ₂)金属熔体前端开始析出固相，此时热平衡方程式为

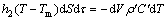                  (6)

式中：h₂为此阶段换热系数；ρ′为金属熔体在T_L到T_k温度范围内的密度，近似地取ρ′=ρ；C′为金属熔体在T_L到T_k温度范围内的摩尔热容，近似地取

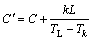                             (7)

式中：L为金属熔体的结晶潜热；k为停止流动时液流前段的固相数量，即为第二阶段充型至固液两相区内的固相数量，从而有

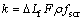                              (8)

式中：f_scr为充型流动临界固相分数，近似取f_scr=0.25^[12]；定义两相区长度。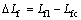

故式(6)可写成

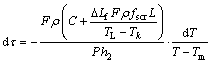           (9)

代入边界条件τ=τ₁时，T=T_L；τ=τ_s时，T=T_k；τ_s为停止流动的时间。式(9)积分后得

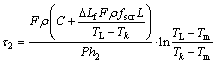         (10)

由式(10)从而有

         (11)

3  仿真基础

仿真采用Flow3D铸造模块，在铸件充型过程数值模拟中，将液态金属熔体看做不可压缩流体，其流动过程服从质量守恒和动量守恒，数学形式为连续性方程和N-S方程^[13]。

1) 连续性方程

                        (12)

2) N-S方程

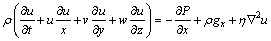
(13)   

3) 能量方程

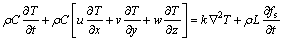    (14)

4  结果讨论

4.1  充型流动长度分析

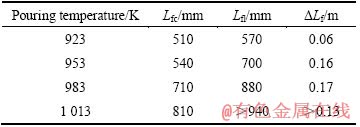
图5和表1所示为压铸实验测量记录得到的在不同浇注温度下薄壁流动试样充型临界长度和极限长度。从图5可以看出，薄壁试样压铸充型临界长度L_fc、极限长度L_fl均随浇注温度的升高而增加，两相区长度ΔL_f也随浇注温度的升高而增加(浇注温度为1 013 K时，充型已经充填满流动试样并充型至压铸试样中央壁厚处，此处体积远大于流动试样体积)。

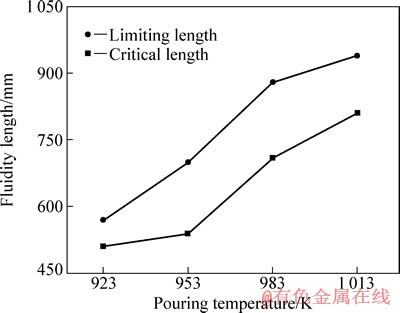
图5  流动试样充型长度随浇注温度的变化

Fig. 5  Change of fluidity length of fluidity specimen with pouring temperature

表1  不同浇注温度下的流动试样充型长度

Table 1  Fluidity length of fluidity specimen with pouring temperature

实验AlSi10MnMg铝合金为典型的结晶温度很宽的合金，在过热热量散失尽以前，以纯液态流动；当温度下降到液相线以下时，液流中析出晶体，顺流前进，并不断长大，液流前段不断与冷的型壁接触，冷却最快，晶粒数量最多，使金属熔体的黏度增加，流速减慢，当晶粒达到某一临界数量时，便结成一个连续的网格，液流的压力不能克服此网格的阻力时，发生堵塞而停止流动，充型完成^[11]。当金属液流动时，金属熔体的黏性及型壁对其的阻滞作用使金属熔体在型壁面法相方向上形成速度梯度，造成金属熔体流层之间产生摩擦，再加上其内部质点的紊流，消耗了金属熔体的能量。因此，这种作用越强，液态金属消耗的能量越多，充型流动长度就越短^[14]。研究表明，铝合金熔体的黏度随温度的升高而减小^[15]，铝合金熔体的流动性随熔体过热的增大而增强^[16]。提高浇注温度，铝合金熔体的黏度减小，液态金属的流层之间质点产生的摩擦减小，型壁对液态金属的阻滞作用降低，充型过程中阻力减小，流动能力增强，因此充型流动长度增加；同时，较高的浇注温度会增加铝合金熔体的过热，熔体冷却凝固的时间变长，充型时间增加，充型流动长度变长。

4.2  压射冲头运动分析

图6所示为浇注温度为1 013 K通过高速摄像实验记录的压射冲头的位移—时间和速度—时间曲线。图7所示为金属熔体充型至流动试样阶段压射冲头的位移—时间曲线。

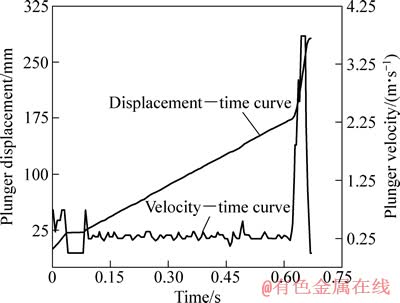
图6  压射冲头的位移—时间和速度—时间曲线

Fig. 6  Displacement—time and velocity—time curves of plunger (1 013 K)

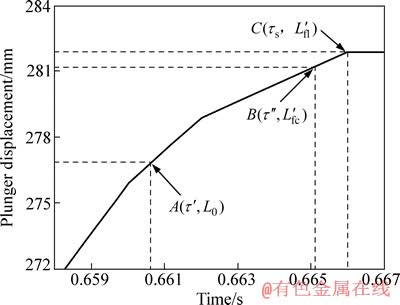
图7  流动试样充型阶段压射冲头的位移—时间曲线

Fig. 7  Displacement—time curve of ram for fluidity specimen (1 013 K)

从图6所示压铸冲头位移—时间曲线可以看出，在约0.620 s时刻，曲线中存在一个明显的拐点，也就是压射冲头由慢转快切换点，在0.620 s之前为慢压射过程，在0.620 s之后为快压射过程，此时刻点略大于初始设定值0.620 s。压铸机为电气液压系统，整个动作的完成都由电气系统控制液压系统完成，系统中开关、阀以及各管道中的高压液压油和高压气体都存在一定程度的滞后和延迟，综合作用的效果使得实际的压射慢-快切换点有约0.020 s的滞后；在约 0.042 s时刻开始，曲线中存在一个长约为0.040 s的平台，此平台表明在这0.040 s时间内压射冲头处于静止状态。在压射前，系统通过电机带动液压泵给主系统提供压力，其它各系统处于待机状态，各机构也处于相对静止，当压射一开始，压射油缸活塞带动压射冲头在压射室内作相对运动，压射冲头和压射室之间的阻力也由静摩擦力转变为动摩擦力，运动需要克服最大静摩擦力这一能量势垒就要求液压系统提供更大的压力，当压射冲头冲破最大静摩擦力能量势垒后加速运动，液压系统的滞后延迟使得加速后的油缸液压油难以瞬间补充，因此，在此时刻压射冲头停止运动，当液压系统供油稳定后，压射冲头继续稳定向前运动。

从图6所示的压射冲头速度—时间曲线可以看出，在压射刚启动阶段，速度变化波动明显，其峰值超出设定值300 mm/s而达800 mm/s，然后在约0.042 s时刻存在一个长约为0.040 s的平台，此平台产生的时间和位移与位移—时间曲线中所示平台一致；然后压射冲头以设定值300 mm/s的速度向前稳定运动，在约0.620 s时刻，快压射蓄能阀门开启，压射冲头转换成快压射，压射冲头速度迅速增加，在约0.656 s时刻达到其峰值约4 100 mm/s，然后速度迅速降低，在约0.670 s时刻速度降为0 mm/s，增速过程用时0.036 s，减速过程用时仅0.014 s。压射冲头在压射室内作相对运动有两种阻力：一种是压射冲头和压射室壁之间的摩擦阻力，另一种是金属熔体流动时的阻力。金属熔体流动时的阻力也由两种形式^[14]：一种是充型中金属熔体的沿程损失，它是由于金属熔体的粘性及型壁对其的阻滞作用，使金属熔体在型壁面法相方向上形成速度梯度，造成金属熔体的流层之间产生摩擦，再加上其内部质点的紊流而形成的；另一种是充型中金属熔体的局部损失，它是由于金属熔体的粘性及流程上流经断面的方向和形状发生变化，流动方向发生变化和流体微团紊动变形而形成的。在实验曲线中可以观察到，其增速过程出现了3个峰才到达其最大峰值，金属熔体流经横浇道、壁厚处型腔时金属熔体流经断面的方向和形状发生了变化，这种变化带来的阻力相当大，直接使得压射冲头的速度降低。当金属熔体流经流动试样型腔时，其壁厚降至1.5 mm，其金属熔体流经断面的方向和形状变化更剧烈，金属熔体损失的能量大大增加，压射冲头速度加速减慢至静止，充型完成。

将图6所示压射冲头位移—时间曲线的末端局部放大，即得到金属熔体在流动试样型腔流动时压射冲头的位移—时间曲线，如图7所示。然后通过图7中的曲线确定实验数据点A(τ′，L₀)、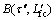和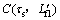，其中：A(τ′，L₀)点为金属熔体充型至流动试样型腔时刻对应的压射冲头运动的(时间，位移)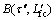；点为金属熔体充型至临界长度时刻对应的压射冲头运动的(时间，位移)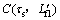；点为金属熔体充型完成即充型至极限长度时刻对应的压射冲头运动的(时间，位移)。

根据压射冲头运动规律有

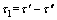                                  (15)

                                 (16)

根据熔体不可压缩原则有

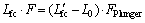                    (17)

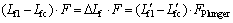       (18)

式中：F_Plunger为压射冲头截面面积。

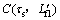点数值从实验图7曲线直接读取，将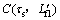点实验值和表1中1 013 K浇注条件下的ΔL_f 值其代入式(18)即可求得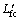；将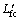值和表1中  1 013 K浇注条件下的L_fc值代入式(17)即可求得L₀；通过L₀、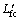直接从图7曲线中读取τ′、τ″，分别代入式(15)和(16)即可求得τ₁、τ₂。同理，可获得其它浇注温度条件下的τ₁、τ₂值，表2所列为流动试样在不同浇注温度下的τ₁、τ₂值。

表2  不同浇注温度下流动试样的充型时间

Table 2  Filling time of fluidity specimen at different pouring temperatures

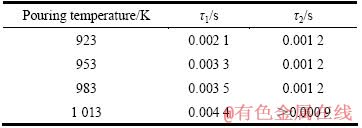
从表2中可以看出，随着浇注温度的升高，流动试样压铸充型第一阶段充型时间τ₁逐渐增长，第二阶段用充型时间τ₂相差无几。较高的浇注温度会增加铝合金熔体的过热，熔体降至液相线温度T_L所需要的也就会时间变长，这和4.1节中充型长度变化因浇注温度升高引起充型时间的增长而增大一致；当温度从液相线温度继续降至停止流动T_k时，由于铝合金熔体降低的温度相同，实验结果显示所需时间相同，那么可以推测在第二阶段固液两相区铝合金熔体有相同的换热状况。

4.3  换热系数计算结果

将表2中τ₁值和浇注温度T_j代入式(5)即可求得第一阶段内的平均换热系数h₁，将表2中τ₂和表1中ΔL_f的值代入式(11)即可求得第二阶段内的平均换热系数h₂，计算各参数值如表3所列，求得的换热系数值如图8所示。

表3  计算中各参数值

Table 3  Related Parameters in calculation

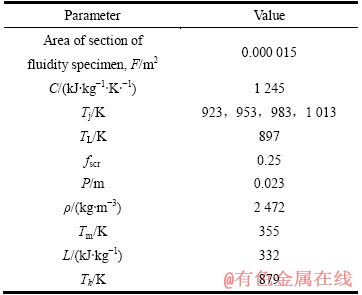
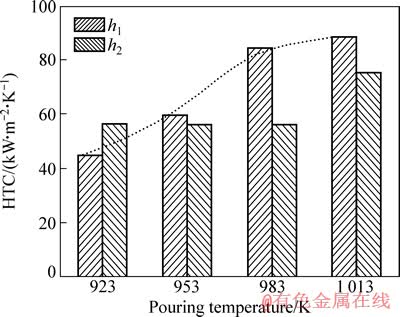
图8  不同浇注温度下流动试样的换热系数

Fig. 8  Heat transfer coefficient of fluidity specimen at different pouring temperatures

从图8可以看出，在第一阶段，换热系数h₁随浇注温度的升高逐渐增大，开始增加较快，后面逐渐减慢；在第二阶段，换热系数h₂随浇注温度的变化影响很小。从式(5)中可以看出：在第一阶段，其换热系数h₁随充型时间τ₁成线性递减关系，随浇注温度T_j成对数递增关系，又充型时间τ₁亦可看做为浇注温度T_j的函数，综合结果，当浇注温度为923~1 013 K时，其换热系数随浇注温度的升高逐渐增大。从式(11)中可以看出：在第二阶段，其换热系数h₂随固液两相区充型长度ΔL_f成线性递增关系，实验结果(见表2)显示在此阶段充型时间τ₂保持不变，计算结果表明在浇注温度为923~1 013 K时，第二阶段浇的换热系数h₂主要和充型时间τ₂有关，固液两相区充型长度ΔL_f对其影响很小。

4.4  仿真结果讨论

将计算求得的换热系数值输入Flow3D铸造模块对薄壁铝合金压铸充型进行仿真分析，对比采用软件默认的换热系数(20 kW/(m²·K))，仿真所用的相关参数如表3所列，表4和表5分别列出采用不同换热系数计算的仿真结果以及实验结果。

表4  充型长度以及充型完成时刻前段温度

Table 4  Filling length and tip temperature during filling process finished

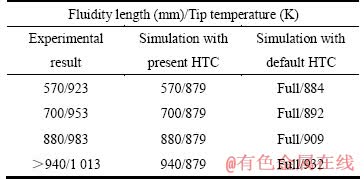
表5  充型实验及仿真结果

Table 5  Filling results of experiment and simulation

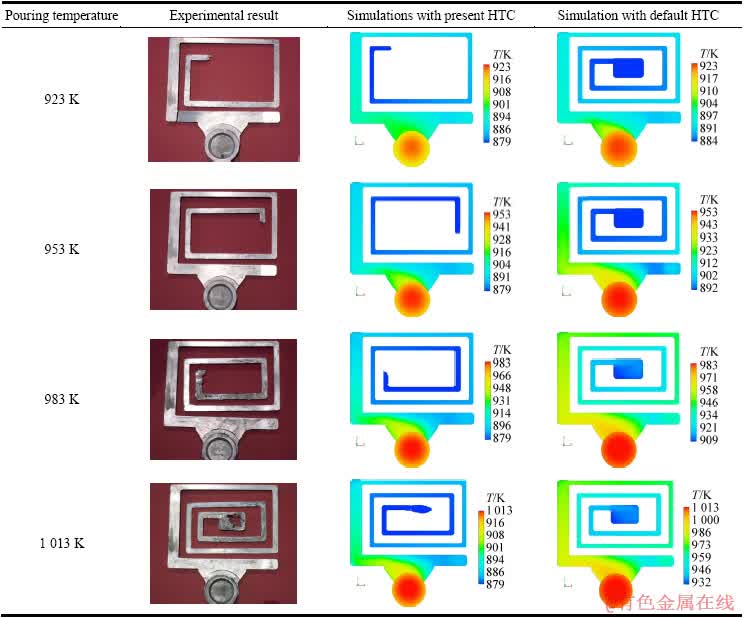
从表4和表5中可以看出，采用本研究方法求得的换热系数进行仿真计算时，仿真结果和实验结果吻合得较好；当采用默认换热系数仿真计算时，熔体都充填满型腔，仿真结果显示与实验结果相差较远。表4统计结果显示，采用本研究方法求得的换热系数进行仿真计算时，当熔体前段温度降至停止流动温度T_k时，熔体停止流动、充型完成；当采用默认换热系数进行仿真计算时，熔体充满型腔时其前段温度都高于停止流动温度T_k，这表明熔体还可以继续充型，其充型长度和充型结果与实验结果相差较远。因此，在薄壁铝合金压铸充型过程中，采用本研究所用方法获得的换热系数进行仿真计算时，其仿真结果更能准确地模拟真实充型过程，这对优化此类大型复杂薄壁铝合金的压铸充型工艺有很大的帮助，也对准确预测此类铸件在充型过程中可能产生的浇不足、冷隔等缺陷提供了参考。

5  结论

1) 流动充型长度随浇注温度的升高而变长。

2) 当充型温度高于液相线温度时，流动充型时间随浇注温度的升高而增长；当充型至温度处于液相线温度至停止流动温度之间时，流动充型时间保持不变。

3) 当充型温度高于液相线温度时，此阶段换热系数随浇注温度的升高而增长；当充型至温度处于液相线温度至停止流动温度之间时，此阶段换热系数随浇注温度变化很小。

4) 采用基于热平衡方程求得的换热系数进行模拟仿真计算时，其仿真结果与实验结果较一致。

ReferenceS

[1] TAUB A I, KRAJEWSKI P E, LUO A A, OWENS J N. The evolution of technology for materials processing over the last 50 years: the automotive example[J]. Journal of the Minerals Metals and Materials Society, 2007, 2: 48-57.

[2] ZHANG Li-qiang, LI Luo-xing, ZHU Bi-wu. Simulation study on the low pressure die casting (LPDC) process for thin-walled aluminum alloy casting with permanent mold[J]. Materials and Manufacturing Processes, 2009, 24: 1349-1353.

[3] FRANKE R, DRAGULIN D, ZOVI A, CASAROTTO F. Progress in ductile aluminum high pressure die casting alloys for the automotive industry[J]. Metallurgia Italiana, 2007, 5: 21-26.

[4] HE Yi, ZHOU Zhao-yao, CAO Wen-jiong, CHEN Wei-ping. Simulation of mould filling process using smoothed particle hydrodynamics[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2684-2692.

[5] DOMKIN K, HATTEL J H, THORBORG J. Modeling of high temperature-and diffusion-controlled die soldering in aluminum high pressure die casting[J]. Journal of Materials Processing Technology, 2009, 209: 4051-4061.

[6] DOUR G, DARGUSCH M, DAVIDSON C, NEF A. Development of a non-intrusive heat transfer coefficient gauge and its application to high pressure die casting effect of the process parameters[J]. Journal of Materials Processing Technology, 2005, 169: 223-233.

[7] ZHANG Li-qiang, LI Luo-xing, ZHU Bi-wu. Inverse identification of interfacial heat transfer coefficient between the casting and metal mold using neural network[J]. Energy Conversion and Management, 2010, 51(10): 1898-1904.

[8] 郭志鹏, 熊守美, 曹尚铉, 崔正吉. 铝合金ADC12高压铸造过程中铸件与铸型间界面热交换系数的研究[J]. 金属学报, 2007, 43(1): 103-106.

GUO Zhi-peng, XIONG Shou-mei, CHO Sang-hyun, CHOI Jeong-kil. Study of interfacial heat transfer coefficient between metal and die during high pressure die casting process of aluminum alloy ADC12[J]. Acta Metallurgica Sinica, 2007, 43(1): 103-106.

[9] RAIMO H, OTTO L, LARS A, HANS I L. The heat transfer during filling of a high-pressure die-casting shot sleeve[J]. Materials Science and Engineering A, 2005, 413/414: 52-55.

[10] DOUR G, DARGUSCH M, DAVIDSON C. Recommendations and guidelines for the performance of accurate heat transfer measurements in rapid forming processed[J]. International Journal of Heat Transfer, 2006, 49: 1773-1789.

[11] 李庆春. 铸造形成理论基础[M]. 哈尔滨: 哈尔滨工业大学出版社, 1983: 35-36.

LI Qing-chun. Theoretical basis of casting process[M]. Harbin: Harbin Institute of Technology Press, 1983: 35-36.

[12] FLEMINGS M C. Solidification processing[M]. London: McGraw Hill, 1974.

[13] REIKHER A, BARKHUDAROV M R. Casting: An analytical approach[M]. London: Springer-Verlag London Limited, 2007.

[14] 杨裕国. 铝压铸成型及质量控制[M]. 北京: 化学工业出版社, 2009: 55-57.

YANG Yu-guo. Process and quality control of Aluminum die-casting[M]. Beijing: Chemical Industry Press, 2009: 55-57.

[15] DINSDALE A T, QUESTED P N. The viscosity of aluminum and its alloys-A review of date and models[J]. Journal of Materials Science, 2004, 39: 7221-7228.

[16] RAVI K R, PILLAI R M, AMARANATHAN K R, PAI B C, CHAKRABORTY M. Fluidity of aluminum alloys and composite: A review[J]. Journal of Alloys and Compounds, 2008, 456: 201-210.

(编辑  何学锋)

基金项目：国家“十二五”科技支撑计划项目(2011BAG03B02)；国家自然科学基金资助项目(51075132)；高等学校博士学科点专项科研基金资助项目(20090161110027)

收稿日期：2012-11-22；修订日期：2013-03-15

通信作者：李落星，教授，博士；电话：0731-88821950；E-mail：llxly2000@163.com