预应力锚索地梁结构在边坡稳定中的作用机理

何美丽，刘霁

(湖南城市学院 土木工程学院，湖南 益阳，413000)

摘要：建立受非均布线形荷载作用的地基力学模型，应用叠加原理推导出预应力锚索–地梁结构中垂直于梁轴线平面内的地基中深度z处的应力和位移计算公式，为研究预应力锚索–地梁结构在岩体中的传力规律提供理论依据。以溆怀(湖南溆浦—怀化)高速公路K24+233~K27+89边坡为实险区域研究预应力锚索地梁结构在边坡稳定中的作用机理。研究结果表明：在对锚索施加预应力后，锚索预应力通过地梁传递给被加固的岩土体，在垂直于地梁轴线的平面内，其传递方式以梁轴线与该平面的交点为端点的近似橢圆的等值面形式由内向外呈逐渐衰减趋势分布；两地梁周边岩体中的压应变随深度增加由小到大增至峰值，然后逐渐衰减为0，这种分布形式与理论结论一致。

关键词：预应力锚索-地梁结构；叠加原理；非均布线形荷载；下滑应力；边坡加固

中图分类号：TD313          文献标志码：A         文章编号：1672-7207(2013)06-2543-06

Force transmission law of prestressed anchor-rope and groundsill structure in slope stability

HE Meili, LIU Ji

(College of Civil Engineering, Hunan City University, Yiyang 413000, China)

Abstract: The force transmission law of a prestressed anchor-rope and the groundsill structure in rock mass were studied. The foundation mechanical model of nonuniform linear unipoium load under the premise of the ground surface suffering nonuniform linear load was established and deduced by the superposition principle, and the calculating formula for the stress and displacement at the depth z in the foundation of the beam axis was deduced for the prestressed anchor-rope and groundsill structure. Taking the slope of K24+233—K27+89 of Xupu—Huaihua Expressway as a experimental region, the force transmission law of prestressed anchor-rope and groundsill structure in slope stability were studied. The results show that when the anchor cable is provided with pre-stress, the actual prestress in the prestressed cable anchor can be transferred to the strengthening geotechnical body through the ground beam, of which the transfer mode tends to decay from the inside to the outside in the form of approximate ellipse iso-surface with the endpoints. The intersection of the beam axis and the plane are perpendicular to the axis of the beam. The compressed strain in the peripheral rock of two ground beams tends to increase with the increase of the depth of the anchor, and then tends to decay gradually and finally tends to be 0 after reaching its peak value. This distribution form is in accordance with the theoretical form.

Key words: prestressed anchor-rope and groundsill structure; superposition principle; nonuniform linear load; stress of downslide; slope consolidation

预应力锚索-地梁是预应力锚索和地梁共同构成的一种新型支护体系^[1]，近年来发展很快，被广泛运用于边坡加固。其钢绞线一端锚固在深层地层中，另一端借助锚具锚固在地梁上，通过预应力达到控制被加固坡面变形的目的^[2-5]。地梁能将锚索端头的压力进行扩散传递，并有调整浅层岩土应力的作用。与抗滑桩相比具有以下优点：双向受压结构；施工简单，灵活、速度快，更适用于抢险工程；布置灵活，锚索的长度和地点可以根据钻孔反馈的地质资料进行调整^[6]。目前，对预应力锚索地梁荷载传递规律的研究还主要集中在预应力锚索荷载传递机理和锚头预应力在岩土体中的传递规律上。吕庆等^[1]对破碎岩质边坡的预应力锚固机制进行数值模拟分析得出，锚墩加框格梁的结构形式明显改善了边坡坡体表层的受力和变形状态。丁秀丽等^[5]对具体深基坑工程的拉力型锚杆锚固段黏结应力的分布形态进行现场监测。Nakayama等^[6]研究了荷载从锚索转到灌浆体的力学机制。目前，人们对索体周边剪应力分布规律以及单根锚索预应力在岩土体中的分布规律研究较多^[7-14]，对预应力锚索与地梁组合结构加固边坡时岩体力学传递机制的定量理论分析和力学传递规律的现场试验研究不多。在此，本文作者利用弹性理论推导在预应力锚索加载后预应力通过地梁在岩土体中的传递机制，并以湖南溆怀(湖南溆浦—怀化)高速公路K24+233~K27+89左边坡作为现场试验地点，验证预应力锚索–地梁结构传力机制的理论分析结果的正确性。

1  预应力锚索-地梁结构的传力规律

空间半无限体表面受法向集中力P作用的力学模型如图1所示。将地基看成是1个具有水平表面且沿3个空间坐标(x，y，z)方向无限延伸的均质弹性体。设此地基表面作用1个竖向集中力P，用Boussinesq弹性力学方法求解此集中力在地基中引起的应力和位移。半空间弹性体内任意1点M(x，y，z)的竖向应力和位移为：

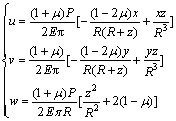        (1)

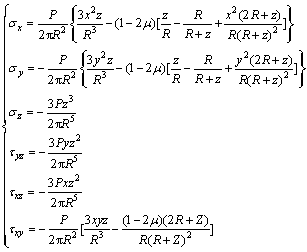 (2)

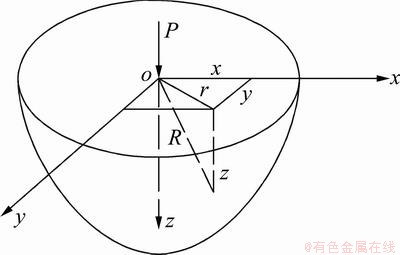
图1  空间半无限体表面受法向集中力P作用的力学模型

Fig. 1  Mechanical model of spatial semiinfinite bod surface under function of normal concentrated force P

式中：σ_x，σ_y，σ_z，τ_yz，τ_xz和τ_xy为各应力分量(MPa)；E为岩体弹性模量(MPa)；μ为岩体泊松比。当集中力P₁，P₂和P₃作用在地基中任意点M时，应用叠加原理则可以计算地表的应力s_z和位移w。

地基受非均布线形荷载作用的力学模型见图2。当地基表面作用于一非均布的线形荷载P=f(x)时，梁中间垂直于梁轴线平面内的地基中深度z处的M点的应力和位移计算公式可采用微元和应力叠加原理推导得出：

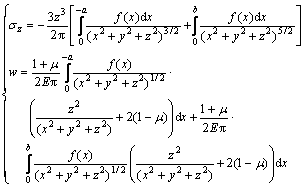                       (3)

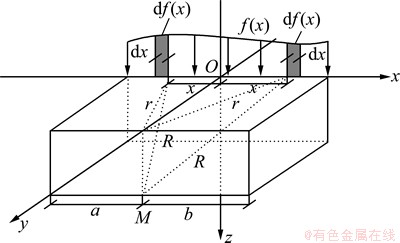
图2  地基受非均布线形荷载作用的力学模型

Fig. 2  Mechanical model of foundation under nonuniform linear load

2  预应力锚索地梁荷载传递规律的现场试验

2.1  试验边坡地质概况

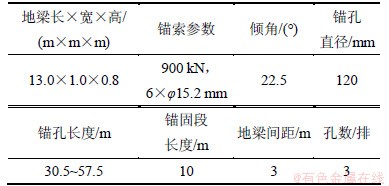
试验地点在湖南溆怀高速公路K24+233~K27+89左边坡。该边坡位于走向为SN38°左右的长条形山丘，坡面宽度为326.0 m，坡顶高程为176.7 m，坡脚最低标高为121.0 m，高差为55.7 m，自然山坡坡比为1:1.23；该山丘两侧冲沟最低标高为117.0 m。该坡面与岩层倾向属于逆向坡，风化层上厚下薄，属于强风化页岩边坡。坡面岩层覆盖层为块石质土，厚度为0.5~2.5 m，岩石内摩擦因数为0.5，容许承载力为300 kPa。地梁物理参数如下：混凝土弹性模量E_c=2.55×10⁴ MPa，地梁摩擦力μ_c=0.167 MPa。试验点锚索地梁设计参数见表1。

表1  工点锚索地梁设计参数

Table 1  Anchor-rope and groundsill design parameters of industrial point

2.2  仪器布设与连接

应变测孔布设在地梁一侧与地梁轴线垂直，每个观测断面设3孔，深度各不相同，水平间距为0.6 m。在每眼测孔中的不同深度共埋设应变测点5个，每测点具体位置与应变计编号见图3。

试验的主要目的是观测地梁在施加预应力后应变在岩体内部的分布规律。观测地梁为2-4和2-9共2根，每根地梁上均作用着3根600 kN的预应力锚索。在每根地梁的一边分别布设3个观测孔，地梁2–4的观测位置设在梁中间与梁轴线垂直的平面内，地梁2-9的观测位置设在距梁端2 m且垂直于梁轴线的平面内。测量仪器采用长沙金码公司生产的检测仪；选用ZX-215A型弦式数码应变计测量应变，分辨率为1 me，最大量程为±1 500 me，观测仪器为JMZX-3006智能振弦数码检测仪。

2.3  试验结果与分析

对应变的观察在锚索施加预应力后进行，每天分早上和下午2次，连续观察5 d。早上观察环境气温平均为27 ℃，下午为39 ℃，平均温差为12 ℃。图4~5所示分别为地梁2-4和2-9工作锚在距其0.6，1.2和2.0 m位置上应变沿深度的分布曲线。由于应力同应变具有相同的分布形式，所以，通过对应变分布曲线进行观察和分析就可以判断应力的分布规律。由图4~5可以看出：地梁2-4和2-9周边岩体中的应变沿深度的分布曲线基本一致；压应变(负值)随深度增加由小到大增至峰值，然后逐渐衰减为0。这种分布形式与理论推导出的距施力点不同位置岩体中的应力分布曲线形式基本相同。

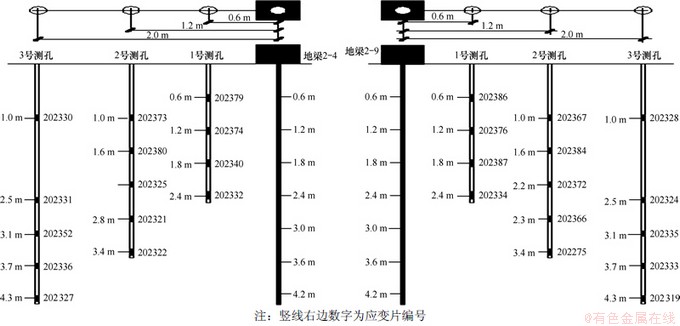
图3  各应变测孔应变计布设情况

Fig. 3  Layout of strain gauge to each strain measuring holes

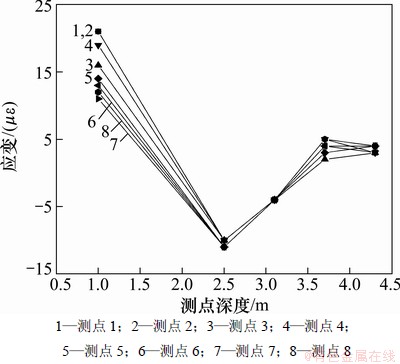
图4  地漂2-4中3号测孔(即2-4-3)应变分布

Fig. 4  Strain distributions of measuring hole of 2-4-3

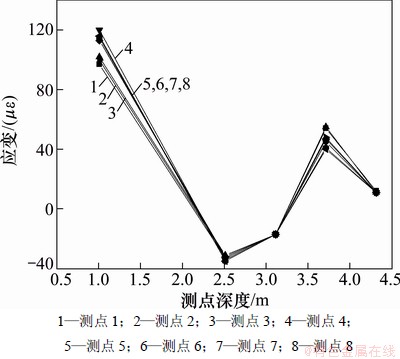
图5  地漂2-9中3号测孔(即2-9-3)应变分布

Fig. 5  Strain distributions of measuring hole of 2-9-3

从图4和图5可以看出：应变在第1个测点处都不同程度地出现了拉应变。这可能是由于测孔距工作锚距离较远(已达2.0 m)，压应力分布距离小于测控距离，岩体中单位面积上的下滑应力超过压应力，造成该位置处的岩体产生一定程度的拉应变。这从另一方面也说明了岩体中应力等值线分布形式的正确性。其中，第1个测点距工作锚孔较远，处于压应力较小的椭圆形等值面中。这说明尽管施加了预应力锚索地梁加固，但坡面上一定范围和深度内仍然存在拉应变，可能造成浅层岩土体滑移或坍塌。这就是在单根地梁间加横梁加固边坡的原因。此外，应变观察值的离散程度较大，这可能是边坡岩体受温度影响所致。因为每天2次观察是在早上和下午进行的，2次观察环境温差平均高达12 ℃，所以，环境气温对观察结果产生了一定影响，但这对应变沿不同深度的分布趋势并不造成较大影响。

3  工程实例的理论计算

在对湖南溆怀高速公路K24+233~K27+89边坡防止边坡滑移的设计中，采用预应力锚索配合地基梁加固页岩强风化岩质边坡。锚索施加的预应力P=600 kN，沿梁长度方向设3孔锚索：在中心部位设1处，其余2处分别设在距梁左、右端各2 m处。地梁和被加固岩土体各强度参数如下：岩土体基床系数k=2.24×10⁷ N/m³，岩土体弹性模量E=1.6 GPa，泊松比μ=0.39；混凝土弹性模量E=2.55×10¹⁰ Pa，泊松比μ=0.167；地梁宽度b=0.4 m，高度h=0.5 m。

采用双参数地基模型计算地基反力，如图6所示。将计算的各点地基反力用二次多项式拟合，得到地基反力(y)与梁长度(x)之间的关系式为

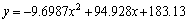       (4)

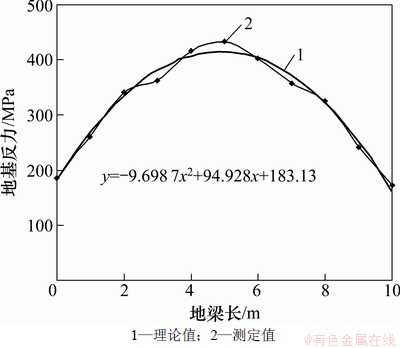
图6  地基土反力图

Fig. 6  Anti-force graphs of foundation soils

将式(4)代入(3)，计算与梁轴线垂直的平面内各点的应力与位移。令岩土体中应力分别为0.5 MPa和0.1 MPa，计算岩土体中的应力等值线；令位移分别为0.1 mm和0.05 mm，计算岩土体中的位移等值线。计算结果分别见图7和图8。

令(4)式中y分别为0.4，0.8和1.2 m，经计算，可以作出距地梁轴线不同距离处岩土体中应力和应变沿深度的分布曲线图，见图9和图10。

通过理论分析计算可以得出：对锚索施加预应力后，锚索预应力通过地梁传递给被加固的岩土体，其传递方式在垂直于地梁轴线的平面内，是以梁轴线与该平面的交点为端点的近似橢圆的等值面形式(见图6)由内向外呈逐渐衰减趋势分布；位移等值面在岩土体中的分布形式(见图8)与应力的分布形式不同，它不经过原点，而是与岩土体表面相交，也就是说，预应力在岩体表面所产生的位移不为0 mm，在施力点处最大，往远处逐渐衰减为0 mm。在垂直于梁轴线平面内，距梁轴线不同距离处岩土体中的应力及位移的分布(分别见图9和图10)具有以下特点：应力在岩体表面位置处为0 MPa，往内不断增加达到峰值，然后开始逐渐衰减直至为0 MPa，距离施力点越远，应力分布曲线越平缓；位移则在岩体表面位置处分布较大而不为0 MPa，往内不断增大达到峰值，然后开始逐渐衰减直至为0 MPa；距离施力点越远，位移分布曲线越平缓。

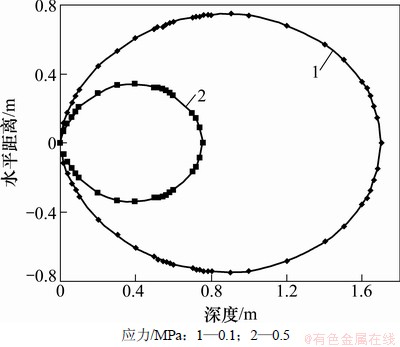
图7  不同应力时岩体中等值应力分布

Fig. 7  Equivalent stress distribution map in different stresses situation in rock mass

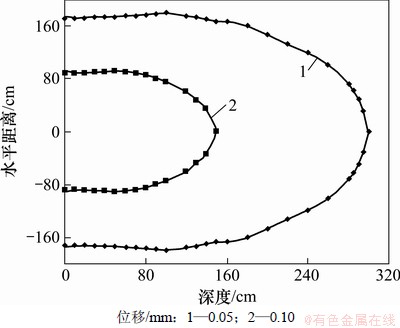
图8  不同位移时岩体中等值位移分布

Fig. 8  Equivalent displacement distribution map in different displacements in rock mass

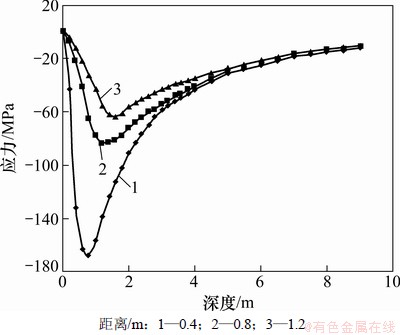
图9  距地梁不同距离处岩体中的应力分布曲线

Fig. 9  Stress distribution curves of different distances to ground beam in rock mass

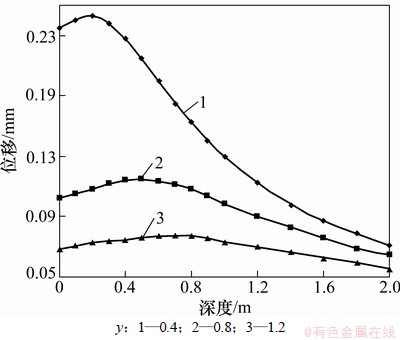
图10  距地梁不同距离y处岩体中的位移分布曲线

Fig. 10  Displacement distribution curves of different distances to ground beam in rock mass

岩体应力的现场试验结果与理论分析结果基本一致，这说明锚索施加预应力后岩体中的应力分布确实遵循这一规律，同时也证明关于应力在岩体中分布机制理论分析的正确性。

4  结论

(1) 锚索施加预应力后通过地梁传递给被加固的岩土体，其传递方式在垂直于地梁轴线的平面内，并且以梁轴线与该平面的交点为端点的近似橢圆等值面形式由内向外呈逐渐衰减趋势分布。

(2) 施加了预应力锚索地梁被加固，但是，在坡面上一定范围和深度内仍然存在拉应变，可能造成浅层岩土体滑移或坍塌。

(3) 预应力锚索-地梁周边岩体中的压应变随深度增加由小到大增至峰值，然后逐渐衰减为0，这种分布形式与理论结论一致。

参考文献：

[1] 吕庆, 孙红月, 尚岳全. 预应力锚索框格梁体系加固破碎岩质边坡合理间距研究[J]. 岩石力学与工程学报, 2006, 25(1): 136-140.

L Qing, SUN Hongyue, SHANG Yuequan. Study on proper interval of prestressed cables in reinforcing crush rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(1): 136-140.

[2] 程良奎. 我国岩土锚固技术的现状与发展[C]//岩土工程中的锚固技术. 北京: 地震出版社, 1992: 27-61.

CHENG Liangkui. China’s rock anchor of the status quo and development of technology[C]//Geotechnical Engineering Technology Anchor. Beijing: Earthquake Publishing House, 1992: 27-61.

[3] 李德芳, 张友良, 陈从新. 边坡加固中预应力锚索地梁内力计算[J]. 岩土力学, 2000, 21(2): 170-172.

LI Defang, ZHANG Youliang, CHEN Congxin. Design of prestressed-cable sommer for slope-reinforcing engineering[J]. Rock and Soil Mechanics, 2000, 21(2): 170-172.

[4] 夏雄, 周德培. 弹性地基上预应力锚索地梁内力的计算方法[J]. 铁道标准设计, 2005(1): 46-48.

XIA Xiong, ZHOU Depei. A method of internal force calculation on prestressed anchor cable beam on winkler elastic foundation[J]. Railway Standard Design, 2005(1): 46-48.

[5] 丁秀丽, 盛谦, 韩军, 等. 预应力锚索锚固机理的数值模拟试验研究[J]. 岩石力学与工程学报, 2002, 21(7): 980-988.

DING Xiuli, SHENG Qian, HAN Jun, et al. Numerical simulation testing shudy on mechanism of prestressed anchorage cable[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(7): 980-988.

[6] Nakayama M, Beaudoin B B. A novel technique determining bond strength developed between cement paste and steel[J]. Cement and Concrete Research, 1987, 22(3): 478-488.

[7] Goto Y. Cracks formed in concrete around deformed tension bars[J]. Journal of American Concrete Institute, 1971, 68(4): 244-251.

[8] Hansor N W. Influcence of surface roughness of prestressing strand on band performance[J]. Journal of Prestressed Concrete Institute, 1969, 14(1): 32-45.

[9] Fuller P G, Cox R H T. Mechanics load transfer from steel tendons of cement based grouted[C]//Fifth Australasian Conference on the Mechanics of Structures and Materials. Melbourne: Australasian Institute of Mining and Metallurgy, 1995: 32-48.

[10] 宋从军, 周德培, 肖世国. 预应力锚索地梁的内力计算[J]. 岩土力学, 2002, 23(2): 242-245.

SONG Congjun, ZHOU Depei, XIAO Shiguo. Application of prestressed anchor-rope and groundsill to slope stability[J]. Rock and Soil Mechanics, 2002, 23(2): 242-245.

[11] 徐年丰, 牟春霞, 王利. 预应力岩锚内锚段作用机理与计算方法探讨[J]. 长江科学院院报, 2002, 19(3): 45-47.

XU Nianfeng, MU Chunxia, WANG Li. Exploration on working mechanism and calculating method of inner bonding section of prestressed cables within rock mass[J]. Yangtze River Scientific Research Institute from Internet, 2002, 19(3): 45-47.

[12] 李海光. 新型支挡结构设计与工程实例[M]. 北京: 人民交通出版社, 2004: 318-327.

LI Haiguang. Example of design and engineering in new branch notch structure[M]. Beijing: People’s Communications Publishing House, 2004: 318-327.

[13] 赵明阶, 何光春, 王多垠. 边坡处理技术[M]. 北京: 人民交通出版社, 2003: 123-125.

ZHAO Mingjie, HE Guangchun, WANG Duoyen. Slope treatment technology[M]. Beijing: People’s Communications Publishing House, 2003: 123-125.

[14] 郑西贵, 张农, 薛飞. 预应力锚杆锚固段应力分布规律及分析[J]. 采矿与安全工程学报, 2012, 29(3): 365-370.

ZHENG Xigui, ZHANG Nong, XUE Fei. Study on stress distribution law in anchoring section of prestressed bolt[J]. Journal of Mining & Safety Engineering, 2012, 29(3): 365-370.

(编辑  陈灿华)

收稿日期：2012-10-10；修回日期：2012-12-24

基金项目：国家自然科学基金资助项目(50774092)；湖南省科技计划项目(2011SK3128)

通信作者：何美丽(1979-)，女，湖南桃江人，讲师，从事土木工程及工程项目管理的教学与研究工作；电话：13907371370；E-mail：18829203@qq.com