DOI: 10.11817/j.issn.1672-7207.2015.12.030
隧道不同损伤衬砌套拱加固对比试验研究
刘学增1,王煦霖2,何本国3
(1. 同济大学 测绘与地理信息学院,上海,200092;
2. 中铁第一勘察设计院集团有限公司,陕西 西安,710043;
3. 同济大学 土木信息技术教育部工程研究中心,上海,200092)
摘要:研制马蹄形隧道套拱加固模型试验加载装置,对衬砌任意位置加载,在损伤衬砌受力同时进行套拱加固,实现了衬砌“二次受力”试验过程。采用破坏性模型试验,研究松动荷载作用下,不同损伤状态衬砌套拱加固构件变形特性、力学响应、加固效果和破坏模式。研究结果表明:衬砌结构刚度随荷载增加逐渐退化,衬砌承受极限承载力时,套拱加固后承载力提高86%;衬砌在剩余承载力13.8%时套拱加固后,极限承载力提高110%。起拱线以上30°位置可作为地层抗力分界线,加固时机越早,最终破坏荷载越高。套拱加固构件呈延性破坏,关键控制截面是拱顶和拱脚;拱顶易发生大偏心压弯破坏,建议增加套拱拱顶内侧纵向配筋,提高抗拉承载力;拱脚出现压剪破坏,应增设套拱拱脚箍筋,以提高抗剪切能力。
关键词:套拱加固;损伤衬砌;二次受力;刚度退化
中图分类号:TU312 文献标志码:A 文章编号:1672-7207(2015)12-4610-08
Comparative experiment of reinforcement of lining under different damage states with arch surround for tunnel
LIU Xuezeng1, WANG Xulin2, HE Benguo3
(1. College of Surveying and Geo-informatics, Tongji University, Shanghai 200092, China;
2. China Railway First Survey and Design Institute Group Co. Ltd., Xi’an 710043, China;
3. Civil Engineering Information Technology Research Center of Ministry of Education,
Tongji University, Shanghai 200092, China)
Abstract: The loading device of model test for horseshoe section tunnel was manufactured. The device could load any position of lining and its reinforcement. Reinforcement with arch surround strengthened cracking lining under mechanic state. The destructive model tests were carried out to investigate deformation characteristic, ultimate load, reinforced effect and failure mode under different damage states. The results show that stiffness of structure declines with the increase of the load. Capacity of reinforcement with umbrella arch increases 86% when original lining bears ultimate capacity. When the redundant capacity is 13.8%, the cracking lining is reinforced. The ultimate capacity increases 110%. The position of 30° above springline can be deemed as separatrix of strata resistance. If the reinforcing time is earlier, the final damage load is more. The reinforcement presents ductile failure. The crucial controlled section is arch and arch-footing. The arch is vulnerable to compressive-bent damage of large eccentricity. Loop reinforcements inside of arch are increased to improve tensile ability of the cross section. Shear compression appears at wall-footing. Stirrup at wall-footing should be supplemented to update shear capacity.
Key words: reinforcement with umbrella arch; cracking lining; secondary loading; stiffness degradation
在隧道加固方法中,套拱是广泛采用的加固方法。随着运营时间推移,衬砌结构使用功能呈非线性下降,外力作用导致隧道衬砌结构开裂、渗漏水、剥落剥离等[1]。其中,衬砌裂损最为常见,据不完全统计,因外力作用诱发的衬砌损伤比例高达40%。衬砌裂缝的出现直接影响了结构安全性能,特别是外力作用引起的开裂,不仅削减了截面有效高度,而且因截面存在较高的应力、应变水平,致使结构承载力降低,给隧道正常运营带来潜在的风险[2]。不同损伤衬砌套拱加固效果差别较大,针对此问题,国内外学者进行了一些研究工作,取得一定研究成果[3]。汪波等[4]采用模型试验,研究了衬砌背后空洞对结构变形、破坏模式以及补强方案、加固效果。陈旭光等[5]建立扩展有限元数值力学模型,研究了隧道衬砌裂缝扩展过程、分布规律以及影响因素。针对衬砌结构开裂,徐世烺等[6]通过解析方法描述衬砌裂缝起裂过程,推导了基于断裂力学的裂缝宽度计算式、衬砌应力强度因子和断裂参数。还有工程师从现场调研隧道衬砌损伤程度、发展方向和对比现有加固方法[7-8]。但现行隧道设计规范对衬砌开裂没有给出加固方法,更没有提出明确规定[9]。从现有成果看,损伤状态直接影响加固效果和维修成本,公路隧道套拱补强效果及破坏过程的研究则很少[10-12]。模型试验大都是基于一次受力隧道加固,将衬砌加载破坏并完全卸载,套拱施作前衬砌不受荷,其受力模式可以看作是1次受力,不符合套拱加固过程中原衬砌一直受荷的真实状态。现有数值模拟、理论推导难以模拟衬砌开裂过程[13]。鉴于此,本文作者研制马蹄形断面隧道套拱加固的模型试验加载装置,在实现带缝衬砌承载的同时,进行套拱加固。开展不同损伤状态衬砌套拱加固裂缝扩展1:10破坏性对比试验,以期更好地指导运营期间隧道损伤衬砌二次加固,提高结构的使用年限。
1 试验设计
1.1 模型试验装置
模型试验在同济大学自行研制的全周加载装置上进行,该装置由加载系统、量测系统、反力系统组成,如图1所示。模型相似比为1:10,衬砌和千斤顶受力通过弹簧来传递,弹簧端部曲板与衬砌接触,曲板曲率与衬砌一致。原型衬砌截面采用时速80 km双车道四心圆断面隧道,衬砌厚度为0.40 m,衬砌跨度为11.86 m,高度为9.53 m。
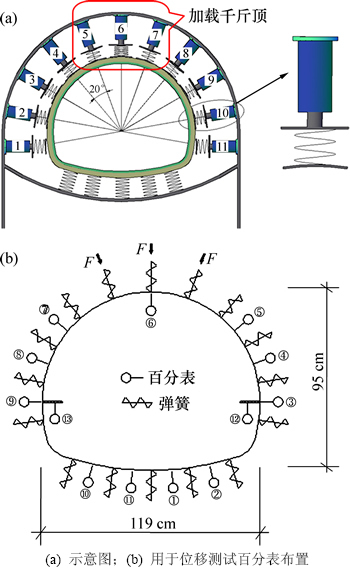
图1 “二次受力”模型试验装置与加载系统
Fig. 1 Device of model test for secondary loading and loading system
松动荷载采用5号、6号、7号3个千斤顶(加载)实现;其余千斤顶不主动加载(反力系统),其弹性抗力模拟围岩与衬砌相互作用,以模拟地层被动抗力;所有主动加载与被动抗力装置一起构成了加载系统。研制的模型试验加载装置可对衬砌和套拱加固构件任意位置施加松动荷载,在结构受荷同时进行套拱加固,即保持衬砌破坏受力状态基础上进行套拱补强加固。待养护结束后,再进行加荷至破坏,解决了隧道结构损伤加固试验中的二次受力“瓶颈”问题,可较真实模拟松动荷载作用的衬砌结构受力特征。将衬砌加载破坏并完全卸载、套拱加固,再加载破坏的“一次受力”模式不符合带缝衬砌套拱加固真实破坏受力过程。
1.2 相似比与测试系统
1.2.1 材料相似比
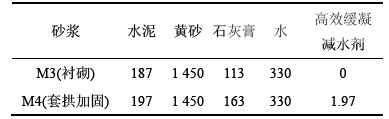
混合砂浆由水泥、黄砂、石灰膏和水配合而成, 2种砂浆M3和M4成分的质量见表1。M3砂浆用于浇筑隧道二衬,M4砂浆用于浇筑套拱,因套拱厚度较小,浇筑较难,为增加砂浆流动性,特加入水泥质量分数为1%的萘系缓凝减水剂。
表1 衬砌与套拱主体结构砂浆成分质量
Table 1 Mortar mixing proportion of lining and umbrella arch kg
根据《公路隧道设计规范》,配有HRB335钢筋的C30受弯构件,配筋率在0.02%~0.20%之间。模型钢筋网由焊接镀锌网制成,焊接镀锌铁网是用优质低碳钢丝排焊而成,焊点牢固,加工性能良好。
1.2.2 位移量测
沿隧道外侧,布置百分表测量隧道的位移和变形,百分表布置如图1(b)所示。11只表用于测量衬砌表面法向的位移;编号 和
和 的表布置在起拱线两端,测量起拱线下沉位移,其测量杆平行于测点处衬砌表面的切向。在拱顶3个千斤顶前端平板和曲板上布置百分表,测量弹簧压缩量和压缩系数的乘积,即拱顶千斤顶的松动压力。
的表布置在起拱线两端,测量起拱线下沉位移,其测量杆平行于测点处衬砌表面的切向。在拱顶3个千斤顶前端平板和曲板上布置百分表,测量弹簧压缩量和压缩系数的乘积,即拱顶千斤顶的松动压力。
1.2.3 松动荷载的施加
依据围岩的级别,确定弹簧刚度,试验采用Ⅵ级范围内较差的围岩。松动荷载采用图1(a)中拱顶3个千斤顶(5号、6号、7号)完成,荷载范围分布在拱顶60°范围内。模型试验荷载是指单个千斤顶的顶力F,逐级加载,每级荷载60 N所对应的原型拱顶压力强度 ,每个千斤顶分担长×宽为0.300 m×0.207 m的区域,可换算成原型隧道衬砌结构松动荷载:
,每个千斤顶分担长×宽为0.300 m×0.207 m的区域,可换算成原型隧道衬砌结构松动荷载:
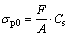 (1)
(1)
式中: 为对应的原型拱顶压力;F为千斤顶的松动压力;A为每个千斤顶分担的面积;Cs为模型试验相似比。根据式(1)求得荷载为9.662 kPa。
为对应的原型拱顶压力;F为千斤顶的松动压力;A为每个千斤顶分担的面积;Cs为模型试验相似比。根据式(1)求得荷载为9.662 kPa。
1.3 模型试验工况
先浇筑和完成养护二次衬砌,加载导致衬砌损伤。保持衬砌损伤受力状态下,浇筑套拱加固并养护,再加载至破坏。每组试验约3月。
为研究公路隧道不同损伤衬砌套拱加固效果,选择2种损伤状态进行套拱加固:1) 损伤衬砌结构承受极限荷载力,不能继续施加荷载,此时进行套拱加固,再加载至破坏。2) 衬砌损伤严重时套拱加固,选择剩余极限承载力13.8%时,再加载至破坏。这2种工况分别表示套拱在极限荷载、破坏严重条件下,模拟套拱补强效果。
2 衬砌结构破坏过程
拱顶3个千斤顶同时逐级加载,拱腰外侧在第7荷载步时,单个千斤顶试验荷载F达到420 N时衬砌开裂。第10荷载步,F=600 N,拱顶正中裂缝张开较明显,深度达31 mm;拱腰外侧产生裂缝,在起拱线以上0°~40°范围均有分布,隧道左右两侧对称,拱腰最大深度可达26 mm;仰拱裂缝分布密集,但张开不明显。荷载步13时,荷载F达到780 N,此后,每级增加30 N。荷载F达到870 N。此时进行套拱加固,对应原型的拱顶松动压力强度为140.1 kPa。
持荷30 min后,拱顶有少量钢丝断裂声响,千斤顶顶力随之降低,拱顶主裂缝深度达31 mm,宽度由0.3 mm增至0.6 mm。1 h后,钢筋大量断裂,发出较大声响,裂缝宽度急剧扩大至2~4 mm;深度在31 mm深处向右侧斜向发展,并几乎贯通衬砌截面,达38 mm,外侧受压区压溃,示意图如图2所示。拱顶破坏后,主裂缝钢筋断裂,无法继续加载,表面原衬砌结构极限荷载为870 N。
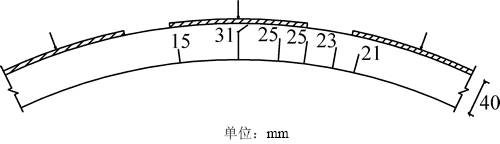
图2 原衬砌在极限荷载时拱顶裂缝深度示意图
Fig. 2 Sketch map of crack of lining at arch before reinforcement
2.1 不同损伤状态下套拱加固破坏过程
2.1.1 衬砌承受极限荷载时套拱加固
在初始荷载达到870 N时,保持荷载不变,套拱施作之前内表面凿毛,刷水等工序,然后进行套拱浇筑。待套拱养护达到1月后,再施加荷载,松动荷载达1 560 N,套拱拱顶主裂缝深27 mm,进入衬砌范围,宽约0.1 mm。荷载至1 620 N,套拱主裂缝深39 mm,宽度达0.5 mm;持荷30 min之后,套拱主筋突然断裂,拱顶截面破坏,套拱主裂缝与衬砌既有主裂缝相汇合,截面外侧在加固之前,已经压溃,衬砌钢筋已经拉断。并且左、右两拱脚,也在破坏后出现斜裂缝。套拱加固构件拱脚部分发生斜裂纹,处于压剪力学状态,建议施加箍筋,提高抗剪承载力。
拱顶破坏后拱腰裂缝分布如图3所示。从图3可以看出:对比拱腰外侧裂缝分布范围,加固前衬砌既有裂缝分布在起拱线以上0°~40°范围内,加固后最高可至起拱线以上50°范围内。拱顶发生大偏心压弯破坏,建议增加纵向配筋,提高抗拉承载力。与衬砌裂缝不同的是,套拱裂缝一旦出现,即到达衬砌,并张开明显。所有部位均未出现套拱与衬砌叠合面间破坏,套拱与原有衬砌叠合面附近存在衬砌钢筋,钢筋在加固前受压,加固隧道在拱顶破坏前,拱腰裂缝深度不会延伸至套拱层,拱腰加固截面尚有较大剩余承载力。
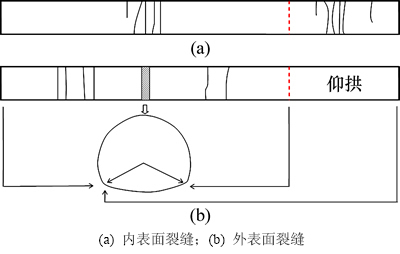
图3 极限荷载下套拱加固衬砌构件裂缝图(虚线为压溃区)
Fig. 3 Cracks unfolded drawing for reinforced lining with umbrella arch under ultimate load (dashed line represents collapse)
2.1.2 衬砌损伤严重时套拱加固
原衬砌剩余承载力13.8%时(拱顶荷载为750 N),停止衬砌加载,准备施作套拱。此时,对应原型的拱顶松动荷载为120.8 kPa,拱顶主裂缝宽度约0.2 mm,拱顶区域裂缝深度示意图如图4所示。
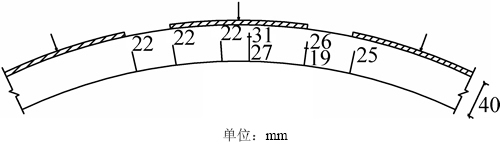
图4 拱顶区域裂缝深度示意图
Fig. 4 Distribution of crack depth of lining at arch
拱顶荷载为1 110 N,拱顶内侧正中率先开裂,深度贯通套拱厚度,到达套拱-衬砌叠合面,与衬砌既有裂缝未对齐,该裂缝与最近的衬砌既有裂缝相距7 mm。拱顶荷载1 170 N,仰拱正中右侧开裂,深度到达套拱与衬砌叠合面。当松动荷载1 710 N时,拱顶正中裂缝与衬砌既有裂缝(未对齐距7 mm)汇合。
拱顶荷载1 830 N,持荷30 min之后,拱顶正中主裂缝突然快速张开,发出清脆响声,钢筋断裂,外侧压溃,截面破坏,而拱顶其余裂缝未见扩展,破坏发生在主裂缝处,加固后隧道达到极限承载力。
隧道破坏以后,为了更好地描绘裂缝位置,将衬砌沿仰拱展开,裂缝素描如图5所示。
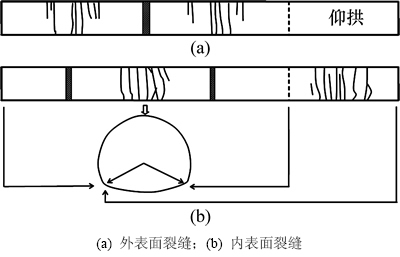
图5 严重损伤时套拱加固衬砌构件裂缝展开图 (虚线为压溃区)
Fig. 5 Cracks unfolded drawing for reinforced lining with umbrella arch under severe damage (dashed line represents collapse)
从图5可以看出,内表面仰拱区域裂缝密集,开裂较早,但是其裂缝不会张开,说明仰拱截面并非关键截面。与拱顶裂缝类似,仰拱区域套拱裂缝间距大于衬砌的裂缝间距,裂缝数量比衬砌的少。拱腰衬砌既有裂缝分布在起拱线以上0°~40°范围内,加固以后新增的裂缝分布在起拱线以上20°~50°范围内。
2.2 套拱加固构件变形特性
2.2.1 衬砌承受极限荷载时套拱加固
衬砌达到极限承载力(荷载870 N)时进行套拱加固,构件全过程变形时程曲线如图6所示。
从图6(a)可以看出:衬砌达到极限承载力(荷载870 N)时,拱顶-起拱线收敛值为12.744 mm,加固前收敛平均斜率为68.3 N/mm。加固后最终破坏荷载1 620 N,拱顶-起拱线收敛值为24.576 mm,收敛平均斜率为125.3 N/mm。加固后拱顶沉降变缓,曲线斜率增大,结构整体刚度明显增加。
从图6(b)可以看出:仰拱位移和荷载近似呈线性关系,曲线在初始荷载870 N附近,出现折点,先降低随后增加,并与原来轨迹重合,表示套拱施作前拱顶应力松弛。仰拱沉降也近似对称,在正中最小,两侧最大,呈对称分布。
从图6(c)可以看出:左右两侧位移呈对称分布,起拱线位置、起拱线以上20°两测点的位移,加固之前,当荷载比较小时,增长较慢;当荷载比较大时,增长较快;套拱加固之后,又变缓。
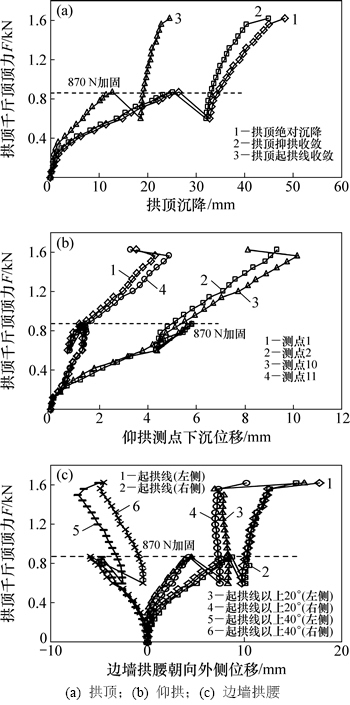
图6 衬砌承受极限荷载(870 N)时套拱加固荷载与位移关系
Fig. 6 Relationship between load and displacement for reinforced lining with umbrella arch under load of 870 N
2.2.2 衬砌损伤严重时套拱加固
剩余承载力13.8%(荷载750 N)时进行套拱加固,构件全过程变形时程曲线如图7所示。
从图7可以看出:加固前(剩余承载力13.8%),拱顶-起拱线收敛值为9.203 mm,收敛平均斜率为81.5 N/mm。套拱加固后构件二次加载破坏时(荷载1830N),拱顶-起拱线收敛值为15.371 mm,收敛曲线平均斜率为175.1 N/mm。加固后曲线斜率增大,结构整体刚度明显增加。
仰拱、边墙和拱腰的位移发展规律与衬砌承受极30°位置可作为地层抗力弹簧分界线。
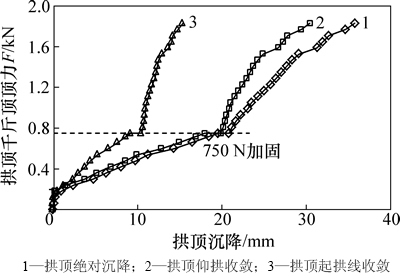
图7 衬砌损伤严重(荷载750 N)时套拱加固荷载与拱顶位移关系
Fig. 7 Relationship between load and displacement for reinforced lining with umbrella arch under load of 750 N
2.3 弹性抗力分布
弹簧抗力可表示隧道主体结构和围岩相互作用关系。
2.3.1 衬砌承受极限荷载时套拱加固
衬砌达到极限承载力时进行套拱加固,加固前初始荷载F=870 N,套拱加固后拱顶千斤顶F=1 320 N、破坏荷载1 620 N弹簧抗力及衬砌法向位移如图8所示。
从图8可以看出:在加固前后,抗力范围基本没有变化,分布在整个边墙区域,及拱腰的起拱线以上小于30°的范围之内。起拱线以上30°位置弹簧,加固前与衬砌脱开,加固后受压,但压力较小,故30°可以作为抗力区域分界线。加固前F=870 N时,最大弹簧抗力854 N,与F比值为0.982;套拱加固后松动荷载F=1 320 N时,最大弹簧抗力1 113 N,与F比值为0.843;F=1 620 N时,最大弹簧抗力1 740 N,与F比值为1.074。
2.3.2 衬砌损伤严重时套拱加固
剩余承载力13.8%时进行套拱加固,待养护完成再加载。破坏荷载1 830 N时地层弹性抗力及衬砌法向位移如图9所示。
从图9可以看出:加固后构件破坏荷载F=1 830 N时,最大弹簧抗力1 004 N,与F比值为0.549;边墙、拱腰向外突出的区域即抗力分布区,拱腰处抗力较小,下部较大。抗力分布在整个边墙区域及拱腰的起拱线以上小于30°范围之内,抗力分布在加固前后基本保持一致。仰拱正中最小,两侧最大,呈对称分布。与图8相比,弹簧抗力分布规律相似,都是起拱线以上30°位置可作为地层抗力弹簧分界线。
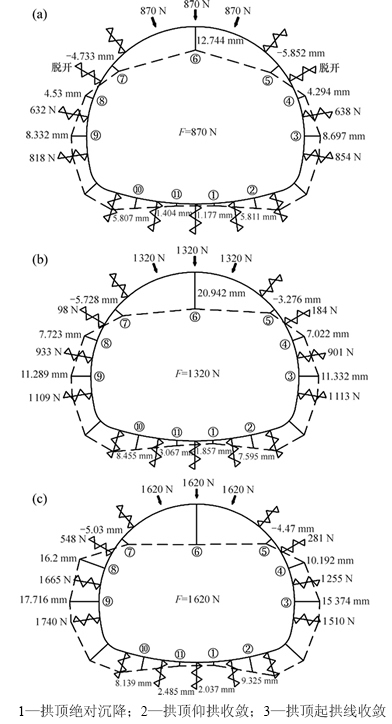
图8 极限荷载下套拱加固结构抗力分布及法向变形
Fig. 8 Resistance and normal deformation of reinforced lining with umbrella arch under ultimate load

图9 严重损伤时套拱加固结构抗力分布及法向变形
Fig. 9 Resistance and normal deformation of reinforced lining with umbrella arch under severe damage
3 不同损伤衬砌套拱加固对比
3.1 隧道开裂与变形过程
不同损伤状态下套拱加固构件开裂、变形与荷载关系如图10所示。
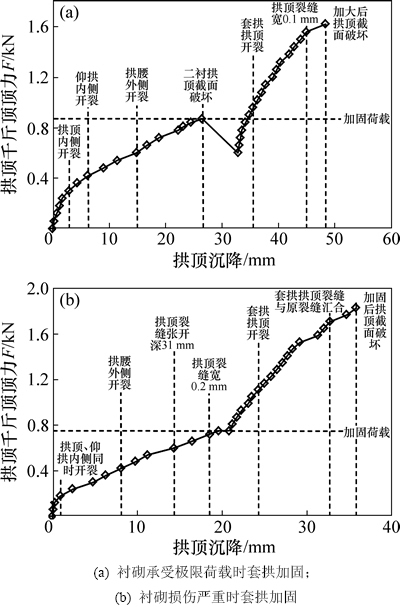
图10 不同损伤衬砌套拱加固变形与荷载关系
Fig. 10 Relationship between load and deformation for reinforced cracking lining with umbrella arch
从图10可以看出:加固前衬砌整体结构刚度随荷载增加而退化,曲线分开裂前弹性段、开裂后曲线段,在临近未加固衬砌破坏时,变形特别大;加固前拱顶内表面首先开裂,其次为仰拱内侧和拱腰外侧开裂;套拱加固后隧道,拱顶正中位置裂缝最终发展成为主裂缝,主裂缝截面钢筋均能拉断,总体呈延性破坏套拱施作期间,由于凿毛、刷水、浇筑等工序的影响,拱顶钢筋断裂,隧道严重受损,千斤顶难以保持荷载,部分卸荷,同时产生很大不可恢复的变形,即图10中下降段。
将加固前后拱顶内表面裂缝进行对比,套拱裂缝间距大于衬砌的裂缝间距,套拱裂缝数量少于衬砌裂缝数量;套拱裂缝一出现深度可穿透套拱,套拱裂缝与原衬砌既有裂缝一般没有对齐,当接近加固后隧道极限承载力时,两者才汇合。
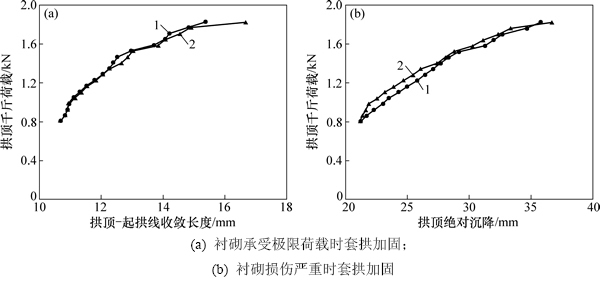
图11 不同损伤状态衬砌套拱加固后变形曲线比较
Fig. 11 Comparison of deformation of lining under different damage states
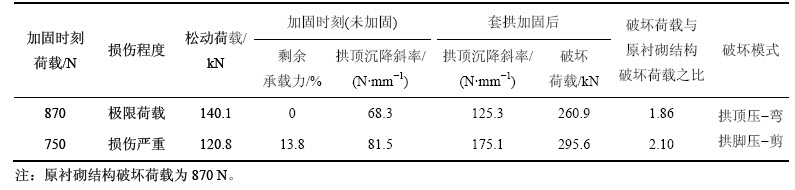
表2 不同损伤状态衬砌套拱加固构件破坏特征
Table 2 Failure characteristics of reinforced lining with umbrella arch under different damage states
加固构件变形与荷载曲线如图11所示。从图11可以看出:两者不同损伤状态加固后曲线移至同一起始点,2种工况轨迹几乎相同,对比加固前的初始荷载,2种工况均属很大荷载甚至拱顶已经破坏。在套拱加固以后,拱顶沉降受初始荷载影响不大,但加固前,拱顶的破坏容易造成难以控制的既有沉降,从安全、套拱浇筑质量以及变形控制角度来看,套拱加固前衬砌仍需一定剩余承载力。
3.2 受力特征比较
根据试验结果,对比2种损伤状态进行套拱加固效果:损伤衬砌承受极限荷载力套拱加固和衬砌损伤严重(剩余承载力13.8%)时套拱加固。根据试验结果,得到变形特性和力学响应如表2所示。
从表2可见:加固前衬砌拱顶破坏,无剩余承载力,加固后承载力为未加固的1.86倍。初始荷载750 N(剩余承载力13.8%)时,加固后承载力为未加固的2.10倍。总体来看,隧道承载力大幅度提高,甚至拱顶严重破坏的隧道,仍能起到良好的加固效果,这说明了套拱加固有效性。加固工况初始荷载越大,加固时机越晚,衬砌损伤越严重,加固后破坏荷载越低。
4 结论
1) 研制了马蹄形断面隧道套拱加固模型试验加载装置,可对衬砌及加固结构任意位置施加荷载。装置在保持损伤衬砌受力状态下进行套拱加固,待套拱养护结束后,再加荷至破坏,解决了隧道衬砌损伤加固试验中二次受力“瓶颈”问题,可较真实地模拟松动荷载作用下衬砌套拱加固构件受力特征。试验装置改变了传统衬砌“加载破坏→完全卸载→套拱加固→再加载破坏”的“一次受力”模式。
2) 套拱加固可有效修复受损隧道,并大幅度提高其承载力,甚至衬砌拱顶严重破坏的隧道仍能起到良好的加固效果。仰拱弹簧反力正中最小,两侧最大,呈对称分布。与衬砌裂缝不同的是,套拱裂缝一旦出现,即到达衬砌,并张开明显。
3) 原衬砌裂缝分布在起拱线以上0°~40°内,套拱加固部分裂缝在起拱线以上50°之内。不论套拱是否加固,起拱线以上30°处可作为抗力弹簧分界线。
4) 衬砌承担极限荷载时,套拱加固后承载力仍可提高86%。加固前变形斜率为68.3 N/mm,套拱加固后变形速率125.3 N/mm。套拱加固构件整体刚度明显增大,直至加固构件破坏,刚度未出现明显减小。
5) 衬砌有13.8%剩余承载力时,套拱加固后极限承载力提高110%。加固前变形斜率81.5 N/mm,套拱加固后变形速率为175.1 N/mm。加固时机越晚,衬砌损伤越严重,加固后构件破坏荷载越低。
6) 在松动荷载下,套拱加固构件延性破坏,关键控制截面是拱顶和拱脚。拱顶易发生大偏心压弯状态,建议增加套拱拱顶内侧纵向配筋,提高抗拉承载力。拱脚出现压剪破坏,应增设套拱拱脚箍筋,以提高抗剪承载力。
参考文献:
[1] 雷明锋, 彭立敏, 施成华. 隧道衬砌刚度对结构耐久性影响的模型试验研究[J]. 中南大学学报(自然科学版), 2012, 43(12): 4865-4872.
LEI Mingfeng, PENG Limin, SHI Chenghua. Damage mechanism and evolution law of mechanical property of tunnel structure suffering sulfate ambient[J]. Journal of Central South University (Science and Technology), 2012, 43(12): 4865-4872.
[2] 冯冀蒙, 仇文革. 隧道衬砌刚度对结构耐久性影响的模型试验研究[J]. 中南大学学报(自然科学版), 2013, 44(9): 3884-3890.
FENG Jimeng, QIU Wenge. Model test on effect of tunnel lining stiffness to structure durability[J]. Journal of Central South University (Science and Technology), 2013, 44(9): 3884-3890.
[3] 钱七虎. 地下工程建设安全面临的挑战与对策[J]. 岩石力学与工程学报, 2012, 31(10): 1945-1956.
QIAN Qihu. Challenges faced by underground projects construction safety and countermeasures[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(10): 1945-1956.
[4] 汪波, 李天斌, 何川, 等. 衬砌减薄对隧道结构承载力影响的模型试验研究[J]. 铁道学报, 2013, 35(2): 106-114.
WANG Bo, LI Tianbin, HE Chuan, et al. Model test of effect of lining thinning on tunnel structure bearing capacity[J]. Journal of the China Railway Society, 2013, 35(2): 106-114.
[5] 陈旭光, 张强勇, 李术才, 等. 基于扩展有限元的深部岩体分区破裂化现象初步数值模拟[J]. 岩土力学, 2013, 34(11): 3291-3298.
CHEN Xuguang, ZHANG Qiangyong, LI Shucai, et al. Preliminary numerical simulation of zonal disintegration phenomenon in deep surrounding rock mass based on extended finite elements[J]. Rock and Soil Mechanics, 2013, 34(11): 3291-3298.
[6] 徐世烺, 刘建强, 张秀芳. 水工有压隧洞衬砌双K断裂理论分析及裂缝宽度计算[J]. 土木工程学报, 2010, 43(1): 114-124.
XU Shilang, LIU Jianqiang, ZHANG Xiufang. Double-K fracture theoretical analysis and crack width calculation of hydraulic pressure tunnel lining[J]. China Civil Engineering Journal, 2010, 43(1): 114-124.
[7] 关宝树. 隧道工程维修管理要点集[M]. 北京: 人民交通出版社, 2004: 38-45.
GUAN Baoshu. Collection of key points for maintenance management of tunnel engineering[M]. Beijing: China Communications Press, 2004: 38-45.
[8] 叶飞, 何川, 夏永旭. 公路隧道衬砌裂缝的跟踪监测与分析研究[J]. 土木工程学报, 2010, 43(7): 97-104.
YE Fei, HE Chuan, XIA Yongxu. Post-construction monitoring and analysis for highway tunnel lining cracks[J]. China Civil Engineering Journal, 2010, 43(7): 97-104.
[9] JTG H12—2003, 公路隧道养护技术规范[S].
JTG H12—2003 Technical specification of maintenance for highway tunnel[S].
[10] Amorim D, Proenca S, Simplified J. Modeling of cracking in concrete: Application in tunnel linings[J]. Engineering Structures, 2014, 70(1): 23-35.
[11] Oriol A, Climent M. Experimental and analytical study of the structural response of segmental tunnel linings based on an in situ loading test, Part 2: Numerical simulation[J]. Tunnelling and Underground Space Technology, 2011, 26(6): 61-72.
[12] 陈卫忠, 田洪铭, 杨阜东, 等. 泡沫混凝土预留变形层对深埋软岩隧道长期稳定性影响研究[J]. 岩土力学, 2011, 32(9): 2577-2583.
CHEN Weizhong, TIAN Hongming, YANG Fudong, et al. Study of effects of foam concrete preset deformation layer on long-term stability of deep soft rock tunnel[J]. Rock and Soil Mechanics, 2011, 32(9): 2577-2583.
[13] 王煦霖. 基于二次受力的山岭隧道套拱加固承载力分析[D]. 上海: 同济大学土木工程学院, 2014: 5-6.
WANG Xulin. Study on bearing capacity of mountain tunnel strengthened by cover arch under secondary loading[D]. Shanghai: Tongji University. School of Civil Engineering, 2014: 5-6.
(编辑 赵俊)
收稿日期:2015-01-15;修回日期:2015-04-12
基金项目(Foundation item):国家自然科学基金资助项目(51278377)(Project (51278377) supported by the National Natural Science Foundation of China)
通信作者:何本国,博士(后),从事隧道工程和岩土工程研究;E-mail:hebenguo@my.swjtu.edu.cn