J. Cent. South Univ. (2020) 27: 1981-1991

DOI: https://doi.org/10.1007/s11771-020-4424-9

Stability analysis of cohesive soil embankment slope based on discrete element method

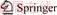
XU Guang-ji(徐光霁)¹, ZHONG Kun-zhi(钟昆志)¹, FAN Jian-wei(范剑伟)¹,ZHU Ya-jing(朱雅婧)¹, ZHANG Yu-qing(张裕卿)²

1. School of Transportation, Southeast University, Nanjing 211189, China;

2. Aston Institute of Materials Research, Engineering Systems & Management Group, Aston University, Birmingham B4 7ET, UK

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: In order to study the safety factor and instability process of cohesive soil slope, the discrete element method(DEM) was applied. DEM software PFC2D was used to simulate the triaxial test to study the influence of the particle micro parameters on the macroscopic characteristics of cohesive soil and calibrate the micro parameters of DEM model on this basis. Embankment slope stability analysis was carried out by strength reduction and gravity increase method, it is shown that the safety factor obtained by strength reduction method is more conservative, and the arc-shaped feature of the sliding surface under the gravity increase method is more obvious. Throughout the progressive failure process, the failure trends, maximum displacements, and velocity changes obtained by the two methods were consistent. When slope was destroyed, the upper part was cracked, the middle part was sheared, and the lower part was destroyed by extrusion. The conclusions of this paper can be applied to the safety factor calculation of cohesive soil slopes and the analysis of the instability process.

Key words: embankment slope; cohesive soil; stability analysis; numerical simulation; PFC2D software; safety factor

Cite this article as: XU Guang-ji, ZHONG Kun-zhi, FAN Jian-wei, ZHU Ya-jing, ZHANG Yu-qing. Stability analysis of cohesive soil embankment slope based on discrete element method [J]. Journal of Central South University, 2020, 27(7): 1981-1991. DOI: https://doi.org/10.1007/s11771-020-4424-9.

1 Introduction

As a supporting structure of the road surface, the embankment has a great influence on the performance of the road. Slope instability is one of the most severe forms of damage to embankment, while slope instability is a very complicated process, including a series of movements such as sliding and translation of the slope soil [1-3]. At present, the mainly methods for studying slope stability are limit equilibrium method and finite element method, which have specific assumptions and limitations. As a traditional method, the limit equilibrium method needs to assume the geometrical position of the sliding surface, divide the slope into several rigid bodies without deformation. It ignores the internal stress-strain relationship and calculates the sliding and anti-sliding force of each rigid block [4-7]. The finite element method has better accuracy than limit equilibrium method in analyzing the slope stability, and it can be used to make up for the drawbacks of the limit equilibrium method for heterogeneous materials. There is no need for slicing or assuming the shape and position of the sliding surface, however, the mechanical properties and stress state at different parts of the slope cannot be taken into account [8-10]. The discrete element method overcomes the limitation of the assumption of macro-continuity in the traditional continuum mechanics model [11-13]. It can simulate the mechanical properties of soil from the meso-point of view, and analyze its macro-mechanical behavior through the study of the meso-parameters of particle structure. The non-continuous numerical method can solve the practical problems of large displacement and nonlinear failure motion [14-17]. At the same time, the motion and displacement of the particle unit can be obtained, which is helpful to analyze the problem from a microscopic point of view [18-21]. The discrete element method is generally an effective numerical simulation method for meso-structure analysis, however, micro parameters between particles should be calibrated based on the macro parameters of the material. The process is complicated, and the accuracy of the calibration affects the reliability of the analysis results. Therefore, micro-parameter calibration is the focus of discrete element analysis [22-25].

The research of slope stability using discrete element method mostly focuses on slope instability mechanism, and the research on safety factor is relatively scarce. ZHOU et al [26] used the discrete element particle flow method to study the safety factors of sandy and cohesive soil slopes, but the calibration process of the micro parameters of the DEM was relatively simple. HE [27] used the particle flow method to study the initiation, propagation, and penetration of cracks in argillaceous soft rock during the pre-peak cyclic loading stage from a mesoscopic perspective. FENG et al [28] used discrete element software PFC2D to study the effects of slope, runoff velocity, particle size, cohesion value of clayey soil, and friction angle φ of sandy soil on the erosion process of slopes. JIN et al [29] created a DEM model to analyze the influence of different rock content, rock shape, spatial structure, and spatial morphology on the stability and failure mode of soil-rock mixture slopes, and revealed the meso-mechanism.

In order to study the safety factor and instability process of cohesive soil embankment slope, PFC2D software was used as the simulation tool in this paper. Firstly, a virtual triaxial test model was established, and the radius enlargement method was used to generate particles. The relationship between micro parameters of cohesive soil discrete element model and macro parameters were obtained through virtual triaxial tests. Afterwards, the micro parameters were repeatedly calibrated by comparing the stress-strain curves which obtained from laboratory and virtual triaxial tests. The Mohr circles of different confining pressures and strength envelope were drawn, and the cohesion and internal friction angle were calculated. The micro parameters of subsequent virtual tests were obtained after iterative attempts. Finally, based on the judgment basis of meso- mechanical slope instability, combined with the theory of strength reduction method and gravity increase method, the slope stability analysis method of DEM was established. The shape and position of the slip surface were obtained by simulations, and the safety factor from both methods were obtained and compared. At the same time, the whole instability process was observed from the microscopic perspective, and the failure form in the slope progressive failure process was analyzed.

2 Micro parameters calibration

2.1 Triaxial test simulation

At present, the mechanical parameters in the discrete element model cannot be obtained through experiments, and there is no obvious unified relationship between micro and macro parameters of cohesive soil. Therefore, it is necessary to calibrate the micro parameters by virtual triaxial test. The parameters are continually adjusted until the results of virtual triaxial test match the results of the actual test. The micro parameters calibrated after adjustment can be used for the next step of the microscopic analysis and other mechanical properties simulation.

The triaxial test in laboratory is also called triaxial shear test. After cutting the soil into cylindrical specimens, the confining pressure is given and kept unchanged, so that the specimens can be destroyed by downward pressure at a constant speed [30-37]. The soil selected in this paper is undisturbed cohesive soil in Nanjing. The physical and mechanical properties of cohesive soil are shown in Table 1, and the particle size distribution curve is shown in Figure 1. The model of triaxial test was established in PFC. The radius enlargement method was used to generate particles. In order to ensure the efficiency of calculation, the gradation of cohesive soil was simplified and the particle size was enlarged. The particle size in the discrete element model was between 5 and 75 mm, and the distribution follows the shape of measured distribution curve in Figure 1. The density of particles was 2650 kg/m³, as the same as the measured soil particle density.

Table 1 Physical and mechanical properties of cohesive soil

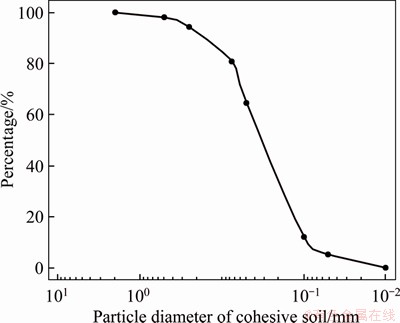
Figure 1 Particle size distribution curve of cohesive soil

The triaxial test specimen is shown in Figure 2. The walls from 1# to 4# enclosing the specimens were generated, after the initial confining pressure was set, the top 3# wall and the bottom 1# wall were used as loading plates to keep the contact stiffness and control the movement speed.

The PFC software simulates the constitutive properties of the material by setting micro constitutive model between particles, including contact-stiffness model, slip model, and bond model. Linear contact-stiffness model and bond model was selected according to the characteristics of cohesive soil at the beginning of virtual test, and slip model is activated when contact-bond model failed during test. Therefore, the meso-parameters of constitutive models which needed to be determined were the friction coefficient μ, the normal stiffness k_n, the tangential stiffness k_s, the normal bond strength n_bond and the tangential bond strength s_bond between particles.

Figure 2 Virtual triaxial test specimen

2.2 Influence of micro parameters

The macro mechanical response of cohesive soil is determined by the micro parameters between particles. The micro parameters should be adjusted according to the macro mechanical properties measured in simulation during the calibration process. Therefore, in order to increase the efficiency of micro parameter calibration, the effects of friction coefficient, contact stiffness and bond strength on the macro mechanical properties were studied. Stiffness ratio and bond strength ratio were set as 1.0 and 2.0 according to experience.

The stress-strain curves under 50 kPa confining pressure with different micro parameters are shown in Figure 3.

The influence of micro parameters on macro parameters obtained from Figure 3 are summarized as follows.

1) As the friction coefficient increases, the peak intensity increases. Since the bond strength model is activated firstly during loading, the sliding model is activated to generate friction only after the bond is broken. Therefore, when the friction coefficient is changed, the initial tangent modulus remains unchanged basically, and the peak modulus increases as the friction coefficient increases.

2) As the contact stiffness increases, the initial tangent modulus increases significantly, and both the peak strength and the axial strain at the peak strength decreases slightly.

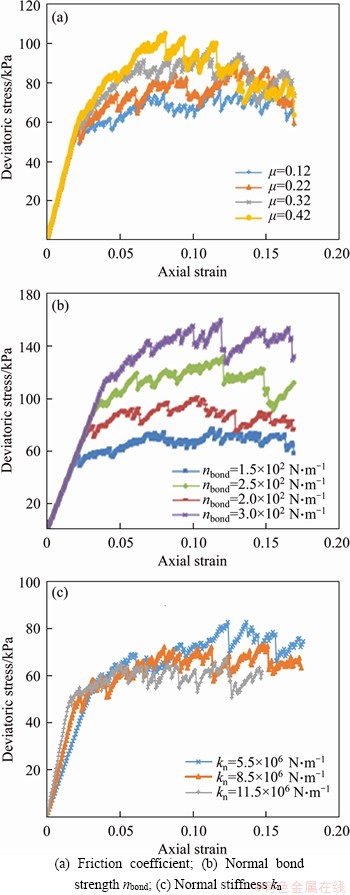
Figure 3 Stress-strain curves with different micro parameters:

3) The bond strength has a greater effect on the overall bias stress. As the bond strength increases, the initial tangential modulus is basically unchanged, but the time requires to break the bond increases significantly, and the peak strength increases accordingly.

2.3 Calibration results

According to the effect of micro parameters on macro parameters obtained above, the micro parameters are adjusted continuously according to the required macro parameters in the calibration process, and the calibration results are shown in Table 2.

Table 2 Micro parameters of particle model

The stress-strain curves from laboratory tests and PFC virtual tests of cohesive soil samples under different confining pressures of 50, 100 and 150 kPa are shown in Figure 4. The stress-strain curve shows weak strain hardening without obvious peak strength. At the beginning, the curve is basically a straight line segment, and the initial tangential modulus is large, showing a certain initial strength, indicating that it is in the elastic phase at the beginning. The fluctuation of the axial strain in the simulation test curve occurs after reaching a certain stress, which is due to the small movement and rearrangement of the particles in the specimen after reaching a certain stress, and the relatively uneven distribution of the internal stress. In the process of virtual shearing, every fracture of bond causes a certain small fluctuation which brings error. However, the deviatoric stress still increases with increasing strain in general. It can be seen from the simulation results under different confining pressures that the curves under three confining pressures matches the laboratory triaxial test results. Compared with the measured value, except for a few points, the error of the simulated value is within 10%, which proves the reliability of the numerical test and the micro parameters obtained.

According to the stress-strain curves of 50, 100 and 150 kPa confining pressure, the Mohr circles and strength envelope are drawn in Figure 5. The shear strength parameters are calculated that the cohesion c=18.1 kPa, and the internal friction angle φ=18.0°. The cohesion c=18.4 kPa and the internal friction angle φ=18.3° in laboratory tests, which also presents good consistency.

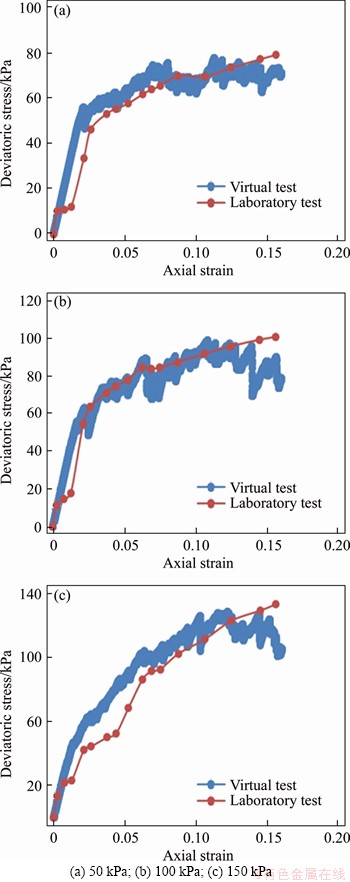
Figure 4 Stress-strain curves under different confining pressures:

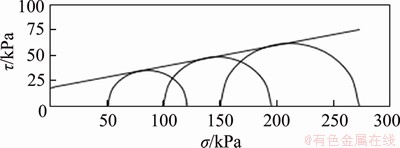
Figure 5 Envelope diagram of shear strength from virtual triaxial test

3 Cohesive soil slope stability simulation

3.1 Stability analysis methods of particle flow slope

The slope instability mainly includes two types: sudden slope instability and progressive failure slope instability [38-40], and progressive slope instability of cohesive soil slope were analysed in this paper. The particle discrete element analysis method is suitable for solving the large deformation and failure problems of geomaterials, facilitating the observation and analysis of the progressive failure process, and reflecting the real process of slope instability more objectively. In this chapter, the stability of slope model is analyzed, the safety factor of slope stability is obtained, and the process of slope instability is studied from the micro perspective by discrete element method of particle flow.

The safety factor is introduced to measure the ability of the slope to maintain stability. Greater safety factors under the same method characterize better slope stability. There are two methods to define the safety factor:

1) The strength reduction method reduces the strength of material to reach the limit equilibrium, so as to determine the strength reduction coefficient of the material. In the stability analysis of cohesive soil slope, the value of c and φ is usually reduced until the slope changes from the initial stable state to the unstable state of failure. The reduction formula is shown in Eq. (1), where c and c′ are cohesions of cohesive soil measured and reduced, φ and φ′ are internal friction angles of cohesive soil measured and reduced.

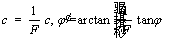                (1)

The safety factor of the slope stability can be defined as shown in Eq, (2).

                           (2)

In the discrete element method, the c and φ values are reduced by the reduction of micro parameters between particles. It can be considered that the cohesion force of soil is provided by the bond strength of particles, and the friction coefficient is directly related to the internal friction angle of soil. Therefore, the following formula can be used to define the safety factor of the slope stability in the discrete element method, where f and f ′ are friction coefficients of cohesive soil measured and reduced, nb and nb’ are normal bond strength of cohesive soil measured and reduced, sb and sb′ are tangential bond strength of cohesive soil measured and reduced [41-43].

                (3)

In this paper, the friction coefficient and bond strength in the discrete element slope model were reduced in proportion at the same time, which means:

                          (4)

2) The gravity increase method is to keep the micro parameters between particles unchanged, increasing the gravity acceleration so the force that soil particles endured is greater than its shear strength, so as to make the slope unstable [41, 42]. The safety factor of cohesive soil slope is defined as shown in Eq. (5), where G and G′ are gravity accelerations measured and increased.

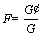                                 (5)

3.2 Establishment of slope numerical model

Based on the particle sizes and micro parameters calibrated in Section 2, the discrete element model of slope is established according to the actual size. As shown in Figure 6, the embankment slope was set as 1:1, the height of the side slope was 10 m, the width of the slope top was 10 m, and the bottom was 25 m. The internal contact force between particles after slope equilibrium is shown in Figure 7. It can be seen that the contact force between the particles on surface and foot of the slope is significantly smaller than that inside the slope, which means progressive slope instability starts on surface and foot, then spreads inside the slope.

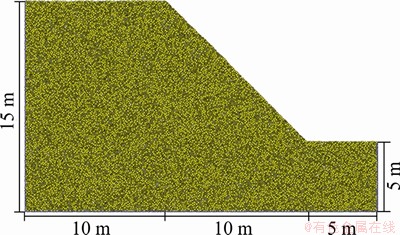
Figure 6 Establishment of slope model

Figure 7 Contact force in slope model

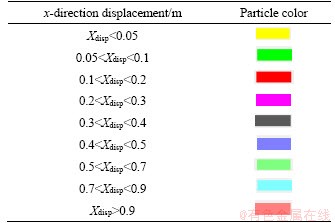
According to the principle of strength reduction method and gravity increase method mentioned above, the connection strength, friction coefficient or gravity acceleration of the soil particles in the model were changed continuously until instability occurred. In order to observe the displacement of soil particle in x direction in the subsequent tests, a program was written with FISH language to make the particles change into different colors after generating different x-direction displacement. The specific color of each particle displacement level is shown in Table 3.

Table 3 Color of different x-direction displacement

4 Results and analysis

4.1 Strength reduction method results

The consistent reduction factor of friction coefficient μ, normal bond strength n_bond and tangential bond strength s_bond was gradually increased from 1.0. When the reduction factor reached 1.39, the displacement of the soil particles in the slope changed greatly, and the slip surface began to appear from the surface of the slope and spread inside gradually. Regarding the reduction factor at this time as the safety factor, the displacement diagrams of particles are shown in Figure 8, from which the entire process of progressive failure of the slope can be clearly seen.

When running 10000 steps, some slope particles have a tendency to move horizontally, mainly concentrated in the middle and lower positions of the slope surface. At this time, the particle movement displacement is small, which is basically within 0.1 m. When running to 30000 steps, the slope shape still maintains the original state, and the soil particles in the slope continues to be displaced. The displacement of the moving particles increases. The maximum x-direction displacement of a few particles have reached 0.4 m, and the range of the moving particles gradually spreads inside the slope. When running 50000 steps, the slip surface continues expanding inside, and the maximum x-direction displacement has reached 0.9 m. At this time, it can be seen that the slope had a relatively obvious arc sliding, the width of slope top has decreased, and the slope has broken.

With the further increase of time step, the sliding of the slope is more and more obvious. The part under the slope shows a bulge, while the width of slope top further reduces. The x-direction displacement of most of soil particles in the sliding plane is more than 0.9 m. When running over 200000 steps, the state of slope basically remains unchanged. It can be considered that the slope have reached equilibrium again when the time step was 200000, and maximum x-direction displacement of soil particles in the slope is 7.727 m.

Analyzing the whole process, when the friction coefficient μ, the normal bond strength n_bond and the tangential bond strength s_bond are reduced by 1.39 times, the shear strength have been reduced to a low extent. Due to the self-weight, the soil in embankment slope slowly reaches its shear strength, the bond between soil particles is weakened. The soil in the middle and lower parts of the slope is the most stressed, and the bond failure occurs first. With the increase of time step, more and more bond failure occurs between soil particles, so the slip surface gradually appears and expands. The deformation of the slope is further accelerated and the sliding is further intensified, resulting in a large-scale landslide until the final equilibrium.

4.2 Gravity increase method results

Keeping the micro parameters of soil particles in the slope unchanged, and multiply the gravity acceleration by the coefficient f which increased gradually from 1.0. When the soil particles have large displacement and obvious slip surface appears, this coefficient f can be regarded as the safety factor of gravity increase method. The safety factor obtained in simulation is 1.67, and the simulation process is shown in Figure 9.

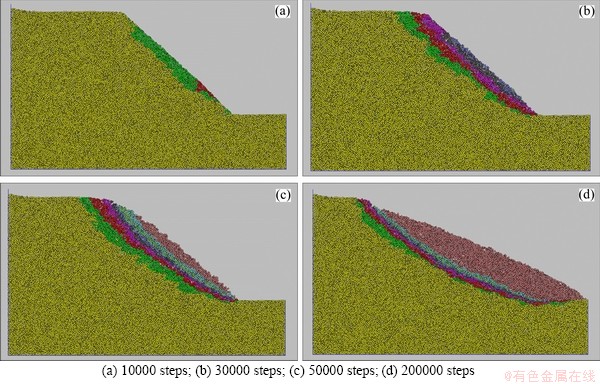
Figure 8 Variation of particle unit displacement at different time steps:

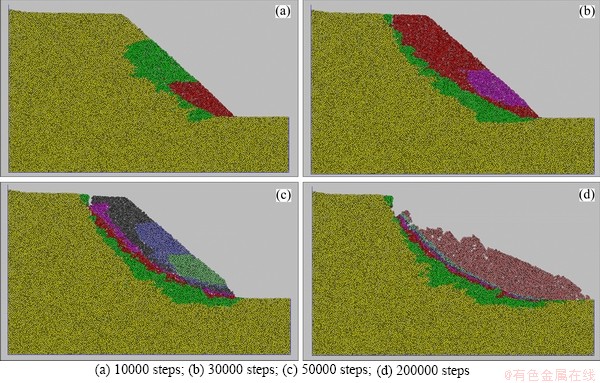
Figure 9 Variation of particle unit displacement at different time steps:

It can be seen from Figure 8 that the process of slope instability under the gravity increase method is similar to that under the strength reduction method. When running 10000 steps, the particles near the slope surface have moved slightly, and it is obvious that the starting position of failure is at the slope foot. At this time, the maximum x-direction displacement in the soil slope is not more than 0.2 m.

With the increase of the time step, the displacement of particles gradually spreads from the foot to the inside of the slope. When the step is 30000, the top of slope is broken, and the arc slip surface is basically formed. When the time step reaches 100000, the slope sliding continues intensifying, and most of the particle displacement reaches 0.9 m. When the step exceeds 200000, the particle displacement changes little, indicating that the slope tends to be stable again, and the maximum x-direction displacement of soil particles is 7.509 m.

4.3 Comparison and analysis

According to the simulation and comparison of the two slope stability analysis methods above, the progressive failure process of the slope could be clearly seen, and the failure trend, maximum displacement and velocity changes obtained by the two methods are consistent. In the final failure, the upper part of slope is cracked, the middle part is sheared, and the lower part is destroyed by extrusion.

The safety factor obtained by the strength reduction method and gravity increase method is 1.39 and 1.67, respectively.

The reason for this extrusion could be analyzed by the shear strength calculation formula as shown in Eq. (6), where τ is shear strength of soil, c is cohesion of soil, σ is normal stress on failure surface and φ is internal friction angle of soil.

τ=c+σtanφ                               (6)

Regarding the strength reduction method, c and φ values are generally used as the shear strength indexes, and the safety factor is calculated by reducing micro parameters between particles in simulation. However, due to the complex relationship in the particle flow model, there is no obvious mathematical equation between micro and macro parameters, or the method of quantitatively converting these parameters directly. Only through the calibration of virtual triaxial test to determine the relationship between the micro parameters and the macro mechanical response. In this paper, although micro parameters are reduced in equal proportion, however, the relationship between micro parameters and macro parameters is not linear, so the values of c and φ are not reduced in equal proportion. Therefore, there is difference between the strength reduction method in this simulation and in traditional theory that reduce c and φ values directly.

The increase of gravity in gravity increase method causes the increase of normal stress σ, so τ increases according to the shear strength formula. Compared with the strength reduction method, the arc-shaped feature of the sliding surface under the gravity increase method is more obvious.

In summary, the strength reduction method weakens the contact between the particles of the slope directly, which is suitable for situations such as immersion instability. Based on this method, the effects of immersion and other conditions on the micro-parameters of the discrete element model of the slope can be further studied, and the slope immersion instability process can be simulated. The gravity increase method is more suitable when the slope is under vertical force, such as when the slope is loaded at the top. Both methods have their own emphasis, and the safety factor obtained by strength reduction method is more conservative.

5 Conclusions

In this paper, PFC2D was used to carry out triaxial test simulation to study the influence of particle micro parameters on macro characteristics of cohesive soil and calibrate the micro parameters of discrete element model. The stability analysis was carried out by the strength reduction method and gravity increase method respectively, and the whole progressive failure process was obtained. The safety factors of the two methods were calculated and compared. The specific research contents and conclusions of this paper are as follows:

1) The micro parameters calibrated in cohesive soil discrete element model are proved to be reliable by comparing the results of laboratory and virtual triaxial test

2) The safety factors obtained by strength reduction method and gravity increase method were 1.39 and 1.67, respectively. The strength reduction method in discrete element simulation reduces micro parameters, and it is different with the traditional strength reduction method which reduce c and φ values directly. Both methods have their own emphasis and application situation, the safety factor obtained by strength reduction method is more conservative, and the arc-shaped feature of the sliding surface under the gravity increase method is more obvious.

3) According to the displacement diagram of particles at different steps during the instability, the whole progressive failure process can be intuitively understood, and the failure trend obtained by the two methods is consistent. When slope is destroyed, the upper part is cracked, the middle part is sheared, and the lower part is destroyed by extrusion.

References

[1] LIU Guo-qiang, YANG Tao, LI Jing, JIA Yan-shun. Effects of aging on rheological properties of asphalt materials and asphalt-filler interaction ability [J]. Construction and Building Materials, 2018, 168: 501-511. DOI: 10.1016/ j.conbuildmat. 2018.02.171.

[2] CHEN An-qi, LIU Guo-qiang, ZHAO Yong-li, LI Jing. Research on the aging and rejuvenation mechanisms of asphalt using atomic force microscopy [J]. Construction and Building Materials, 2018, 167(APR10): 177-184. DOI: 10.1016/j. conbuildmat.2018.02.008.

[3] XIA Wei-yi, DU Yan-jun, LI Fa-sheng, Li Chun-ping, YAN Xiu-lan, ARULRAJAH A, WANG Fei, SONG De-jun. In-situ solidification/stabilization of heavy metals contaminated site soil using a dry jet mixing method and new hydroxyapatite based binder [J]. Journal of Hazardous Materials, 2019, 369: 353-361. DOI: 10.1016/j.jhazmat. 2019.02.031.

[4] ALEJANO L R, FERRERO A M, RAMIREZ- OYANGUREN P, FERNANDEZ M A. Comparison of limit-equilibrium, numerical and physical models of wall slope stability [J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(1): 16-26. DOI: 10.1016/ j.ijrmms.2010.06.013.

[5] ALEXAKIS H, MAKRIS N. Limit equilibrium analysis of masonry arches [J]. Archive of Applied Mechanics, 2015, 85(9, 10): 1363-1381. DOI:10.1007 /s00419-014-0963-6.

[6] MICHALOWSKI R L. Stability assessment of slopes with cracks using limit analysis [J]. Canadian Geotechnical Journal, 2013, 50(10): 1011-1021. DOI: 10.1139/cgj-2012- 0448.

[7] CHEN Jun, ZHANG Dong, HUANG Xiao-ming. Application of discrete element particle flow software (PFC) in road engineering [M]. Beijing: China Communications Press Co., Ltd., 2015. (in Chinese)

[8] MA Tao, ZHANG De-yu, ZHANG Yao, WANG Si-qi, HUANG Xiao-ming. Simulation of wheel tracking test for asphalt mixture using discrete element modelling [J]. Road Materials and Pavement Design, 2018, 19(2): 367-384. DOI: 10.1080/ 14680629.2016.1261725.

[9] ZHOU Jian, JIA Ming-cai. Geotechnical meso-model test and numerical simulation [M]. Beijing: China Science Publishing & Media Ltd.,2008. (in Chinese)

[10] MA Tao, WANG Hao, ZHANG De-yu, ZHANG Yao. Heterogeneity effect of mechanical property on creep behavior of asphalt mixture based on micromechanical modeling and virtual creep test [J]. Mechanics of Materials, 2017, 104: 49-59. DOI: 10.1016/j.mechmat.2016.10.003.

[11] TANG Fan-long, MA Tao, ZHANG Jun-hui, GUAN Yong-sheng, CHEN Li-feng. Integrating three-dimensional road design and pavement structure analysis based on BIM [J]. Automation in Construction, 2020, 113(5): 103152. DOI: 10.1016/ j.autcon.2020. 103152.

[12] ZHANG Yao, MA Tao, LING Meng, ZHANG De-yu, HUANG Xiao-ming. Predicting dynamic shear modulus of asphalt mastics using discretized-element simulation and reinforcement mechanisms [J]. Journal of Materials in Civil Engineering, 2019, 31(8): 04019163. DOI:10.1061/(ASCE) MT.1943-5533.0002831.

[13] WALTON O. Particle-dynamics calculations of shear flow [J]. Studies in Applied Mechanics, 1982, 7(1): 327-338. DOI: 10.1016/B978-0-444-42192-0.50033-5.

[14] MA Tao, WANG Hao, HE Liang, ZHAO Yong-li, HUANG Xiao-ming, CHEN Jun. Property characterization of asphalt and mixtures modified by different crumb rubbers [J]. Journal of Materials in Civil Engineering, 2017, 29(7): 04017036-1-10. DOI: 10.1061/(ASCE)MT.1943-5533.0001 890.

[15] IWASHITA K, ODA M. Micro-deformation mechanism of shear banding process based on modified distinct element method [J]. Powder Technology, 2000, 2(1): 192-205. DOI: 10.2208/journalam.2.401.

[16] ZHANG Yao, MA Tao, DING Xun-hao, HUANG Xiao-ming, XU Guang-ji. Impacts of air-void structures on the rutting tests of asphalt concrete based on discretized emulation [J]. Construction and Building Materials, 2018, 166: 334-344. DOI: 10.1016/j.conbuildmat.2018.01.141.

[17] SHI Dan-da, XUE Jiang-feng, ZHAO Zhen-ying, SHI Ji-yu. A DEM investigation on simple shear behavior of dense granular assemblies [J]. Journal of Central South University, 2015, 22(12): 4844-4855. DOI: 10.1007/s11771-015- 3036-2.

[18] JIANG Ning-jun, DU Yan-jun, LIU Kai. Durability of lightweight alkali-activated ground granulated blast furnace slag (GGBS) stabilized clayey soils subjected to sulfate attack [J]. Applied Clay Science, 2018, 161: 70-75. DOI: 10.1016/j.clay.2018. 04.014.

[19] ZHANG Qiang, XU Wei-ya, LIU Qin-ya, WANG Wei, MENG Qing-xiang. A novel non-overlapping approach to accurately represent 2D arbitrary particles for DEM modelling [J]. Journal of Central South University, 2017, 24(1): 190-202. DOI: 10.1007 /s11771-017-3420-1.

[20] DING Xun-hao, MA Tao, GU Lin-hao, ZHANG De-yu, HUANG Xiao-ming. Discrete element methods for characterizing the elastic behavior of the granular particles [J]. Journal of Testing and Evaluation, 2020, 48: 20190178. DOI: 10.1520/JTE 20190178.

[21] TANG Fan-long, ZHU Shun-chao, XU Guang-ji, MA Tao, KONG Ling-di, KONG Ling-yun. Influence by chemical constitution of aggregates on demulsification speed of emulsified asphalt based on UV-spectral analysis [J]. Construction and Building Matierals, 2019, 212: 102-108. DOI: 10.1016/j. conbuildmat.2019.03.309.

[22] DING Xun-hao, MA Tao, HUANG Xiao-ming. Discrete- element contour-filling modeling method for micromechanical and macromechanical analysis of aggregate skeleton of asphalt mixture [J]. Journal of Transportation Engineering, Part B: Pavements, 2019, 145(1): 04018056. DOI: 10.1061/JPEODX. 0000083.

[23] CAO Ri-hong, LIN Hang, CAO Ping. Strength and failure characteristics of brittle jointed rock-like specimens under uniaxial compression: Digital speckle technology and a particle mechanics approach [J]. International Journal of Mining Science and Technology, 2018, 28(4): 669-677. DOI: 10.1016/j. ijmst.2018.02.002.

[24] CUNDALL P, STRACK O. Discussion: A discrete numerical model for granular assemblies [J]. Géotechnique, 1980, 30(3): 331-336. DOI: 10.1680/ geot.1980.30.3.331.

[25] WANG Cheng, TANNANT D, LILLY P. Numerical analysis of the stability of heavily jointed rock slopes using PFC2D [J]. International Journal of Rock Mechanics & Mining Sciences, 2003, 40(3): 415-424. DOI: 10.1016/S1365- 1609(03)00004-2.

[26] ZHOU Jian, WANG Jia-quan, ZENG Yuan, JIA Min-cai. Slope safety factor by methods of particle flow code strength reduction and gravity increase [J]. Rock and Soil Mechanics, 2009, 30(6): 1549-1554. DOI: 10.1016/S1874- 8651(10)60073-7.

[27] HE Chun-mei. Mechanical behavior of muddy soft rock and dynamic stability of soft-hard interbedded slopes in reservoir area under cyclic loading [D]. Chongqing: Chongqing University, 2018. (in Chinese)

[28] FENG Xing-bo, SONG Dan-qing, XU Yong-fu. Simulation research on characteristics of embankment slope under rainfall scour [J]. Chinese Journal of Underground Space and Engineering, 2018, 14(2): 558-564. (in Chinese)

[29] JIN Lei, ZENG Ya-wu, CHENG Tao, LI Jing-jing. Stability analysis of soil-rock mixture slope based on 3-D DEM [J]. Journal of Harbin Institute of Technology, 2020, 52(2): 41-50. DOI: 10.11918/ 201811110. (in Chinese)

[30] BANERJEE A, PUPPALA A J, HOYOS L R. Suction- controlled multistage triaxial testing on clayey silty soil [J]. Engineering Geology, 2019, 265: 105409. DOI: 10.1016/ j.enggeo.2019.105409.

[31] SAIED M, YVES B, ABDELHAMID B, ULRICH M, BRIAN E. Creep deformation in vaca muerta shale from nanoindentation to triaxial experiments [J]. Journal of Geophysical Research: Solid Earth, 2019, 124(8): 7842-7868. DOI: 10.1029/2019JB017524.

[32] XU Jian-bo, CHEN Jian-ping, JIANG Ping-jiang, CHENG Hu-jin. Investigation of creep behaviors of wudang mica schist by triaxial compression tests [J]. Geotechnical and Geological Engineering, 2019, 37(5): 3831-3842. DOI: 10.1007/s10706-019-00872-7 ISBN: 0960-3182.

[33] MARTINELLI D, TODARO C, LUCIANI A, PEILA D. Use of a large triaxial cell for testing conditioned soil for EPBS tunnelling [J]. Tunnelling and Underground Space Technology, 2019, 94: 103126. DOI: 10.1016/j.tust.2019. 103126.

[34] BOL E, ONALP A, OZOCAK A, SERT S. Estimation of the undrained shear strength of Adapazari fine grained soils by cone penetration test [J]. Engineering Geology, 2019, 261, 105277. DOI: 10.1016/j.enggeo.2019.105277.

[35] LIU Jian-kun, CUI Ying-hui, LIU Xin, CHANG Dan. Dynamic characteristics of warm frozen soil under direct shear test-comparison with dynamic triaxial test [J]. Soil Dynamics and Earthquake Engineering, 2020, 133: 106114. DOI: 10.1016/ j.soildyn.2020.106114.

[36] HE Zhong-ming, XIANG Da, LIU Ya-xin. Triaxial creep test and particle flow simulation of coarse-grained soil embankment filler [J]. Frontiers in Earth Science, 2020: 8. DOI: 10.3389/feart.2020. 00062.

[37] XIA Wei-yi, FENG Ya-song, DU Yan-jun, REDDY K R, WEI Ming-li. Stabilization and solidification of a heavy metal contaminated site soil using a hydroxyapatite based binder [J]. Construction and Building Materials, 2017, 156: 199-207. DOI: 10.1016/j.conbuildmat.2017.08.149.

[38] CHEN Tian, LUAN Ying-cheng, MA Tao, ZHU Jun-qing, HUANG Xiao-ming, MA Si-jia. Mechanical and microstructural characteristics of different interfaces in cold recycled mixture containing cement and asphalt emulsion [J]. Journal of Cleaner Production, 2020, 258: 120674. DOI: 10.1016/j. jclepro.2020.120674.

[39] KOCA T K, KOCA M Y. Comparative analyses of finite element and limit-equilibrium methods for heavily fractured rock slopes [J]. Journal of Earth System Science, 2020, 129: 65-76. DOI: 10.1007/ s12040-019-1314-3.

[40] DING Xun-hao, CHEN Lu-chuan, MA Tao, MA Hai-xia, GU Lin-hao, CHEN Tian, MA Yuan. Laboratory investigation of the recycled asphalt concrete with stable crumb rubber asphalt binder [J]. Construction and Building Materials, 2019, 203: 552-557. DOI: 10.1016/j.conbuildmat.2019.01.114.

[41] WU Hao-liang, JIN Fei, BO Yu-lin. Leaching and microstructural properties of lead contaminated kaolin stabilized by GGBS-MgO in semi-dynamic leaching tests [J]. Construction and Building Materials, 2018, 172: 626-634. DOI: 10.1016/j. conbuildmat.2018.03.164.

[42] TANG Fan-long, MA Tao, GUAN Yong-sheng, ZHANG Zhi-xin. Parametric modeling and structure verification of asphalt pavement based on BIM-ABAQUS [J]. Faculty of Engineering, 2020, 111: 103066. DOI: 10.1016/j.autcon.2019. 103066.

[43] MA Hui, CAI Jing-ming, LIN Zhan, QIAN Shun-zhi, LI V. CaCO₃ whisker modified engineered cementitious composite with local ingredients [J]. Construction and Building Materials, 2017, 151: 1-8. DOI: 10.1016/j.conbuildmat.2017. 06.057.

(Edited by HE Yun-bin)

中文导读

基于离散元法的黏性土路堤边坡稳定性分析

摘要：为了研究黏性土边坡的安全系数和失稳过程，采用离散单元法(DEM)，运用DEM软件PFC2D模拟三轴试验，研究颗粒微观参数对黏性土宏观特性的影响，并在此基础上对DEM模型的微观参数进行标定。采用强度折减法和重力增加法对路堤边坡稳定性进行了分析，结果表明，强度折减法得到的安全系数较为保守，重力增加法下的滑动面弧形特征更加明显。在整个渐进破坏过程中，两种方法得到的破坏趋势、最大位移和速度变化是一致的。边坡破坏时，上部开裂，中部剪切，下部挤压破坏。本文的结论可应用于黏性土边坡的安全系数计算和失稳过程分析。

关键词：路堤边坡；黏性土；稳定性分析；数值模拟；PFC2D软件；安全系数

Foundation item: Project(51808116) supported by the National Natural Science Foundation of China; Project(BK20180404) supported by the Natural Science Foundation of Jiangsu Province, China; Project(KFJ170106) supported by the Changsha University of Science & Technology via Open Fund of National Engineering Laboratory of Highway Maintenance Technology, China; Project(242020R40133) supported by Fundamental Research Funds for the Central Universities, China

Received date: 2020-03-29; Accepted date: 2020-04-26

Corresponding author: FAN Jian-wei, PhD Candidate; Tel: +86-17754094889; E-mail: jianwei_fan@seu.edu.cn; ORCID: 0000-0002- 8257-9823