无人值守传感器网络的一种分布式数据存储算法

肖宜龙^{1, 2}，范明钰¹，王晓京²，蒋海波^{1, 2}

(1. 电子科技大学 计算机科学与工程学院，四川 成都，610054；

2. 中国科学院 成都计算机应用研究所，四川 成都，610041)

摘要：针对无人值守传感器网络的数据存储可靠性问题，提出一种实现简单、性能高效的分布式存储算法。算法采用定向随机游走规则，将网络中的k个源数据包传递到网络中所有的n个节点，网络中的每个节点按一定的概率接收一个新到达的源数据包并将其异或到之前存储的存储数据包中。数值实验表明：存储过程完成之后，即使有部分传感器节点损坏，Sink节点只要收集到任意k+ε，ε≥8个存储数据包，就能计算出原来的k个源数据包；与相关文献提出的基于LT码的方法相比，本算法节省存储过程中各传感器节点约61%的通信成本，同时降低Sink节点约40%的访问成本，具有较好的应用潜质。

关键词：无人值守传感器网络；数据存储；分布式存储算法；随机游走

中图分类号：TP211.9；TP393          文献标志码：A         文章编号：1672-7207(2013)12-4894-09

Distributed data storage algorithm for unattended wireless sensor networks

XIAO Yilong^{1, 2}, FANG Mingyu², WANG Xiaojing², JIANG Haibo^{1, 2}

(1. School of Computer Science and Engineering,University of Electronic Science and Technology of China, Chengdu 610054, China;

2. Chengdu Institute of Computer Application, Chinese Academy of Sciences, Chengdu 610041, China)

Abstract: To solve the data storage reliability problem of unattended wireless sensor networks (UWSN) which is made of n unreliable nodes (k of them are data nodes used to produce source data packets), a new kind of distributed storage algorithm based on random walk was proposed. According to the proposed algorithm, k source data packets were transmitted to every node in the network based on random walk, and every node received a number of source data packets with the given probability and stored the XOR result of them as a stored data packet. The simulation results show that after the storage process is completed, even with some stored data packets missing, the data collector node can successfully recover the k source data packets from any survival k+ε, ε≥8 stored data packets. Compared with LT codes based method, this method reduced network’s communication cost by about 61% and the Sink node’s query cost by about 40%.

Key words: unattended wireless sensor networks; data storage; distributed storage algorithm; random walk

传感器网络^[1]由大量的通信、计算、存储和能量有限的传感器节点组成，集感知、计算、无线通信为一体，通过对物理世界的实时监测，获得用户感兴趣的信息，在民用和军事等领域都有广泛的应用。传感器网络是以数据为中心的网络，其感知数据的存储一直是学术界的研究热点，本文重点研究无人值守传感器网络^[2]的数据存储问题。与一般的传感器网络相比，无人值守传感器网络通常部署在恶劣的环境中，Sink节点(数据收集节点)并不固定在网络中，而是每隔一段时间后才出现在网络中并收集各个数据节点产生的数据包。因此，在Sink节点出现之前，为了避免数据包因节到点损坏而丢失，各数据节点感知到的数据包并不只存储在节点本身，而是采用分布式存储方法存储在整个网络中。无人值守传感器网络的分布式数据存储问题可以简单表述为：如何设计一个有效的分布式存储算法将网络中k个数据节点感知到的k个源数据包存储到网络所有的n个节点中，n＞k。这样，当存储过程完成之后，即使有部分节点损坏进而导致存储其中的存储数据包丢失，Sink节点也能通过任意k个以上未损坏节点的存储数据包还原出原来的k个源数据包。无人值守传感器网络的分布式数据存储算法主要有2类。一类是将每个数据节点的源数据包复制到多个节点中^[2]。这样Sink节出现后，只要每个源数据包都有一个副本可访问，源数据包就不会丢失。这类方法易于执行，但是对传感器节点有限的存储空间是一种挑战。另一类是采用纠删码的编码规则将k个源数据包编码成n个存储数据包，再将n个存储数据包存储到传感器网络的n个节点中^[3-8]。这样，Sink节点出现后，只要能访问到k个以上的存储数据包，就能按照纠删码的译码规则计算出所有的k个源数据包。任伟等^[3-4]提出了基于RS码的方法，这类方法对网络配置要求较高，除了要求每个节点都事先知道网络中其它节点的位置信息外，还要求每个节点必须有较高的计算能力(因为RS码的编码运算是在有限域上进行的)。Aly等^[5]提出了基于Raptor码的方法，但是由于Raptor码是一种级联纠删码，这种方法增加了存储过程的复杂度，不利于实际应用。最具代表性且与本文方法相关的是Kong等^[6-8]提出的基于LT码的方法。这类方法对网络配置要求不高，每个节点只需知道其邻居节点的位置信息即可。存储过程中该方法采用简单随机游走规则将k个源数据包发送到网络中的每个节点；每个节点按照LT码的度分度函数接收一定数量的源数据包并计算得到一个存储数据包存储起来。Sink节点出现后，通过访问这些存储数据包可恢复出原来的所有源数据包。然而该方法有2个方面的缺点：一是简单随机游走的低效率导致每个源数据包都需要传递远比理论值多很多的次数才能遍历网络中的所有节点，因此这增加了网络的通信成本；二是Sink节点为了恢复出所有的k个源数据包，需要访问k(1+λ)个存储数据包(λ＞0，与k的取值有关)；Kong等^[6]的实验表明k的数量级为几百时，k(1+λ)接近2k。因此，这导致了Sink节点的访问成本较高。针对这些问题，基于源数据包传递过程中的定向随机游走规则和网络中每个节点对源数据包的独立计算机制，本文作者提出了一种执行简易，性能高效的分布式数据存储算法。

1  网络模型

与文献[6]中的假设相同，本研究的无人值守传感器网络有如下性质：网络由n个传感器节点构成，其中k个节点为数据节点，每个数据节点用来感知物理量并产生一个大小固定的数据包，称为源数据包，其余的非数据节点只用来存储数据。Sink节点只在源数据包完成存储之后的一段时间内才出现。每个传感器节点都有相同的通信半径，距离小于通信半径的两个节点互称为邻居节点，可以直接通信；处于通信半径之外的节点通过多跳机制间接通信。网络是连通的，任意2个节点都能直接或间接通信。网络中每一个节点都没有一个路由表记录如何与其通信半径之外的节点间接通信，因此2个节点之间的间接通信是通过随机选择中间节点来完成的。

图1所示为本研究的无人值守传感器网络的源数据包存储和访问示意图，图中圆形的点表示数据节点，正方形的点表示非数据节点，矩形的点表示Sink节点，带箭头的线指示了节点之间的通信路径。

图1  无人值守传感器网络示意图

Fig. 1  Unattended wireless sensor network model

为了从理论上分析并在实验中模拟分布式存储算法，本文将无人值守传感器网络抽象为一个二维随机图^[9]。各传感器节点用图中的各顶点表示，若2个传感器节点互为邻居节点，则在图中对应的顶点之间添加一条无向边；由于每个传感器节点都没有路由表，因此一个传感器节点的数据包通过多跳机制传递到另一个节点的过程用随机图上一个随机游走^[9]来表示。

二维随机图及随机游走简明定义描述如下：

二维随机图：在一个单位正方形内随机均匀地放置n个顶点，当任意2个点之间的欧氏距离小于r时(r反映了传感器节点的通信半径)，用一条无向边连接这2个点，这样构成的一个图称为二维随机图，用T(n, r)表示。

随机游走：二维随机图上的一个随机游走定义为按某一随机序列访问图中顶点的过程。一次随机游走开始于某一顶点，并且下一步要访问顶点是从当前访问顶点的邻居顶点中选取的；若下一步要访问的邻居顶点是从当前访问节点的所有邻居顶点中等概率随机选取的，那么这样的随机游走称为简单随机游走。

对于二维随机图T(n, r)，若r满足条件

              (1)

其中：b为一个大于1的常数，那么可以以极大的概率保证图T(n, r)是连通的。

对于一个连通的二维随机图T(n, r)，用t表示随机游走的步数，那么该随机游走访问到的不同顶点数占图中总的顶点数的比例，称为该随机游走对图的覆盖率，用C_t(T)表示；C_t(T)的理论值可以近似的表示为^[10]：

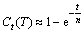              (2)

对于一个连通的二维随机图，从图中任一顶点开始的随机游走如果能够访问图中的所有顶点，也就是对图的覆盖率达到100%，那么该随机游走的平均步数称为图的覆盖时间，用C(T)表示，当式(1)成立时，C(T)可以表示为^[9]：

            (3)

由式(3)可知：当t=O(nln n)时，C_t(T)≈1。

1.1  定向随机游走规则

随机游走有不同的规则，本文算法采用定向随机游走规则^[11-12]在网络中传递每个源数据包，按照定向随机游走规则，每当源数据包到达了当前访问的传感器节点v后，要从v的所有邻居节中选出一个节点u做为下一步要访问的节点。

若N(o)表示任意一个节点o的邻居节点的集合，δ(o)=|N(o)|表示节点o的邻居节点的个数。c(o)表示定向随机游走目前已访问节点o的次数，那么下一步将要访问的节点u的选取过程分为2步：

Step 1: 从当前访问节点v的邻居节点集合N(v)中随机均匀地选择2个节点做为备选节点，它们构成的集合用N^‘表示；

Step 2: 从2个备选节点中选择满足下式的节点u做为下一步将要访问的节点：

           (4)

2  分布式数据存储算法

首先给出算法中用到的参数，本文将这些参数分为2类：一类为间接参数，用来描述网络基本信息和规则，分别如下。

n：表示网络中的传感器节点总数；

k：表示数据节点总数；

d：表示节点通信半径；

N(o)：表示节点o的邻居集合；

δ(o)：表示节点o的邻居个数；

X_j：表示数据节点j的源数据包，j=1，2，…，k；

ID_j：表示源数据包X_j的ID号；

Y_i：表示节点i的存储数据包，i=1，2，…，n；

c_j(i)：表示源数据包X_j已访问节点i的当前次数；

另一类参数影响本文算法的性能，称为直接参数，分别如下。

cnln n：表示传递每个源数据包的定向随机游走的步数，其中c＞1为系数，用变量N记录定向随机游走的当前步数，源数据包每传递一次，N的值增加1；

aln k/k：表示每个节点接收一个新到达的源数据包的概率，其中a＞1为系数。

算法的基本原理如下：

存储过程开始之前: 每个节点(包括数据节点和非数据节点)都存储有一个初始值为0的存储数据包Y_i，大小与源数据包相同。除此之外，每个数据节点都有一个源数据包X_j。

存储过程开始后: 从每个数据节点开始一个步数为cnln n的定向随机游走向前传递该数据节点的源数据包；每当源数据包到达一个新的节点时，新节点按概率aln k/k接收源数据包，并将接收的源数据包异或到自己的存储数据包中；(不论是否接收)新节点然后按照定向随机游走规则将源数据包继续向前传递。当源数据的传递次数达到定向随机游走的给定步数 cnln n后，即N > cnln n 时，源数据包被丢弃，不再向前传递。当所有的k个源数据包都被丢弃后，整个存储过程完成。

2.1  分布式数据存储算法的流程

本文算法的具体实现流程描述为下面的算法1。

算法1：无人值守传感器网络的分布式数据存储算法

输入：k 个源数据包X_v，v=1，…，k。

输出：n个存储数据包Y_u，u=1，…，n。

开始

1:  /*初始化阶段*/

2:     For 每个数据节点 v = 1 to k

3:     为源数据包X_v 添加头信息：ID_v 号及定向随机游走步数计数器 N = 0；

4:     For 每个节点 u = 1 to n

5:     初始化每个存储数据包的值：Y_u = 0；

6:     初始化每个源数据包X_v 已访问节点u的当前次数：

c_v(u)=1，v=1，…，k；

7:  /*分布式存储阶段*/

8:     For 每个数据节点 v = 1 to k

9:     按照概率aln k/k接收X_v，并且更新自己的存储数据包：Y_v=Y_v⊕X_v；

10:    按照定向随机游走规则将源数据包X_v传递到它的一个邻居节点；

11:               c_v(v)=c_v(v)+1；

12:    For 每个节点 u=1 to n

13:    For 每个到达节点u的源数据包X_j

14:    If X_j是第一次访问节点u

15:    节点u按照概率aln k/k接收X_j，并且更新自己的存储数据包：Y_u=Y_u⊕X_j；

16:               c_j(u)=c_j(u)+1；

17:    源数据包X_j更新头信息：N=N+1；

18:               If N＜cnln n，

19:    节点u按照定向随机游走规则将源数据包X_j传递到它的一个邻居节点；

20:               Else

21:    节点u丢弃X_j；

结束

算法1第10和19步中当前节点执行的定向随机游走规则由1.1节中的Step1和Step2定义。

算法1完成之后，网络中不再存储有任何一个源数据包，取而代之的是每个节点都存储了一个存储数据包。

算法1的复杂度简要描述如下。

(1) 通信复杂度。算法1在执行过程中每个源数据包被传递了cnln n次，因此k个源数据包在网络中的通信次数为kcnln n次。

(2) 存储复杂度。算法1执行完成之后，每个节点存储了一个与源数据包大小相同的存储数据包及其计算得到该存储数据包的所有源数据包的ID号。除此之外，算法执行过程中每个节点还记录了各源数据包访问该节点的当前次数，不过算法完成之后这一记录不再存储。

(3) 计算复杂度。由于每个节点按概率aln k/k接收一个源数据包，因此平均情况下，每个节点接收了约k·aln k/k=aln k个源数据包，进行了约alnk次源数据包之间的异或运算。

2.2  分布式数据存储算法的参数及性能分析

算法1中定向随机游走的步数，也就是每个源数据包在网络中的传递次数设置为cnln n的目的是为了保证每个源数据包都能传递到网络中的每个节点；每个节点接收一个新到达的源数据包的概率设置为aln k/k的理由在后文中将会介绍到。下面将分析这2个参数对算法性能的影响。

当算法1执行完成之后，k个源数据包被分布式地存储到了网络的n个节点中，每个节点存储的存储数据包都是若干个源数据包的异或和。

假定Sink节点出现后，随机地从k+ε个未损坏节点中收集了k+ε个存储数据包，其中ε＞0为常数。为便于描述，这k+ε个存储数据包用Y_i，i=1，2，…，k+ε表示。因为每个存储数据包都是源数据包的线性组合，因此，任意一个Y_i，i=1，2，…，n都可以表示为下式(式中的乘法为二元域上的元素与取值在二元域上的向量之间的数乘)：

          (5)

其中：X₁，…，X_k表示k个未知的源数据包，g_i为一个独立的且取值在二元域F₂={0，1}上的随机行向量，称为存储数据包Y_i的生成行向量。由存储算法1可知：g_i的每个元素g_ij，j=1，…，k都是独立取值，且都服从下式定义的分布。

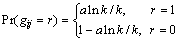         (6)

这k+ε个存储数据包的生成行向量构成了一个(k+ε)×k阶矩阵G_(k+ε)×k，称为k+ε个存储数据包的生成矩阵，即G_(k+ε)×k=[g₁， g₂，…，g_k+ε]^T。借助生成矩阵，这k+ε个存储数据包可以表示为：

           (7)

由线性代数理论可知：若生成矩阵G_(k+ε)×k存在一个可逆k×k阶子矩阵，也就是G列满秩，则式(7)中的方程组存在唯一解(X₁，…，X_k为未知数)，通过解方程组可求得k个未知的源数据包X₁，…，X_k。因此，Sink节点可由任意k+ε个存储数据包计算得到k个未知的源数据包的概率等价于这k+ε个存储数据包的生成矩阵G_(k+ε)×k列满秩，即Rank(G_(k+ε)×k) = k的概率。

2.2.1  算法参数分析

本节给出算法1中每个节点接收一个新到达的源数据包的概率设置为aln k/k，即(G_(k+ε)×k中每个元素取值服从式(6)的原因。

在生成矩阵G_(k+ε)×k中，若存在元素全为0的列，那么G_(k+ε)×k一定是列不满秩的。假定生成矩阵G_(k+ε)×k 中每个元素值为1的概率为ρ，那么为了保证矩阵每一列至少有一个1，有

(8)

令上述概率大于一个趋近于1的小数δ，有

           (9)

由此得出：

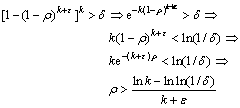   (10)

因此，为了使式(10)成立，本文把矩阵G_(k+ε)×k中每个元素取值为1的概率为ρ的值设置为aln k/k，a＞1为系数；也就是使G_(k+ε)×k中每个元素取值服从式(6)定义的分布。

2.2.2  算法性能分析

用P^failure表示二元域F₂上的生成矩阵G_(k+ε)×k列不满秩的概率，那么，当式(6)成立时，可以得到如下结论：

引理1：当G_(k+ε)×k的每个元素的取值服从式(6)定义的分布时，P^failure的上界为：

(11)

证明：若G_(k+ε)×k的各列线性相关，则G_(k+ε)×k列不满秩，因此

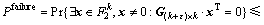
       (12)

令R表示G_(k+ε)×k的任意一个行向量，用w表示向量x中1的个数，因为行向量R的每一个元素取值独立，且取值为1的概率由式(6)定义，因此

   (13)

因为矩阵G_(k+ε)×k的每一个行向量独立，因此G_(k+ε)×kx^T=0的概率为

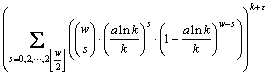(14)

当向量x取所有不同的值时，根据式(12)可得到引理1中的结论。

引理2：当G_(k+ε)×k的每个元素的取值服从式(6)定义的分布且aln k/k = 1/2时，P^failure的上界可以简化表示为：

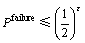            (15)

证明：当ρ=1/2时

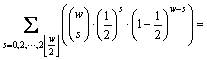
         (16)

不论w的取值为奇数还是偶数，都有

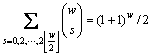         (17)

将式(17)代入式(16)得

            (18)

将式(18)代入式(14)得

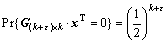      (19)

将式(19)代入式(11)，引理2得证。

表1和表2所列为aln k/k中的参数a，k及ε取不同值时，分别由式(11)和式(15)定义的P^failure的上界在MATLAB环境下的数值计算结果。

表1  a=3.5时P^failure的上界的数值计算结果

Table 1  Numerical results of upper bound of P^failure for a=3.5

表2  a=3时P^failure的上界的数值计算结果

Table 2  Numerical results of upper bound of P^failure for a=3

从表1和表2可以看出：当ε固定时，无论aln k/k是否等于1/2，由式(11)定义的P^failure的上界与式(15)定义的P^failure的上界是近似相等的。当a，ε固定时，P^failure的上界随k的变化不大。因此，P^failure的上界主要由ε决定，可以用式(15)的简化结果近似表示P^failure的上界。

综合上述分析，可用如下定理1描述算法1的性能。

定理1：采用分布式数据存储算法1，Sink节点可由任意k+ε个存储数据包计算得到原来的k个源数据包的概率P满足式(20)：

(20)

特别地，根据数值计算结果，a≥3时，P近似地满足下式：

                 (21)

证明：因为P=1-P^failure，综合引理1，引理2及数值计算结果可得本定理结论。

3  数值实验及分析

本文算法的数值实验是在MATLAB环境下实现的。实验中，在100×100的正方形区域随机均匀的分布了n个点模拟传感器网络各个节点，其中数据节点的比例为设置为30%，即k=0.3n，网络中每个节点的通信半径d满足条件d²=2ln n/(πn)·10⁴(这一条件保证了网络以极大的概率是连通的)。

实验分为2个部分：第1部分实验测试定向随机游走的步数与网络覆盖率之间的关系，称为源数据包传递性能实验；第2部分实验测试存储过程完成之后，Sink节点需要访问多少个存储数据包才能恢复出原来的k个源数据包，称为源数据包恢复性能实验。

3.1  源数据包传递性能实验

每个源数据包都采用随机游走规则在网络中传递，按照式(2)，当随机游走的步数为t时，网络覆盖率的理论值近似为1-e^-t/n。特别地，当t=O(nln n)，即t=cnln n时，源数据包将以极大的概率遍历网络中的每个节点，网络的覆盖率达到1-e^{-cnln n/n}≈100%。实际的应用中，在网络覆盖率达到理论近似值的前提下，源数据包传递次数越少，即t=cnln n的值越小就越能节约网络的通信能耗，因此实验中主要测试系数c的变化对网络覆盖率的影响，并寻找网络覆盖率达到理论近似值1-e^-t/n时，系数c的最小值。

做为对比，实验中比较了简单随机游走规则和定向随机游走规则对源数据包传递性能的影响。

图2和图3所示为n和k取不同值，即不同网络规模条件下，且随机游走步数t分别设置为t=cn和t=cnln n时的数值实验结果。

从图2和图3可以看出：采用定向随机游走规则，k个源数据包对网络覆盖率平均值的实验数值与理论数值1-e^-t/n是近似相等的，而且当源数据包传递次数大于2nln n时，即c大于2时，所有的k个源数据包都覆盖了网络中所有的节点，而采用简单随机游走规则，k个源数据包对网络覆盖率平均值的实验数值明显小于理论数值1-e^-t/n，而且只有当随机游走步数大于4.5nln n时，即c大于4.5时，所有的k个源数据包才能覆盖网络中所有节点。因此采用定向随机游走规则的源数据包传递方法性能更优，在实际应用中，要使网络覆盖率达到100%时，c的最小值可设置为2。

图2  源数据包传递性能测试(随机游走步数t=cn)

Fig. 2  Source data packet transmitting performance for t=cn

图3  源数据包传递性能测试(随机游走步数t=cnln n)

Fig. 3  Source data packet transmitting performance for t=cnln n

3.2  源数据包恢复性能实验

实验测试当存储过程完成之后，Sink节点需要访问多少个存储数据包才能计算出所有的源数据包，也就是测试下面定义的2个变量之间的关系。

源数据包恢复开销η：Sink节点访问的存储数据包个数h与源数据包个数k之差，即η=h-k。

源数据包恢复成功率S：Sink节点能够从h个访问到的存储数据包计算出k个源数据包的概率。

实验中采用定向随机游走规则传递每个源数据包，每个源数据包的传递次数设置为2nln n。

图4和图5所示为n和k取不同值，且每个传感器节点接收一个新到达的源数据包的概率aln k/k的系数a分别设置为a=2(图4)和a=3(图5) 时源数据包恢复成功率S与源数据包恢复开销η之间的关系。

从图中可以看出：实验中当Sink节点收集到的存储数据包个数大于k+8时，也即源数据包恢复开销η达到k+8-k=8时，能计算出k个源数据包的概率S达到了100%；这恰好验证了定理1的结论，即：无论网络规模，也就是无论n和k取值如何，只要每个传感器节点接收一个新到达的源数据包的概率服从式(6)定义的分布，理论上Sink节点可由任意k+ε个存储数据包计算得到原来的k个源数据包的概率S近似大于1-2^ε，当ε=8时，理论上S近似大于1-2⁸≈99.6%。

3.3  性能比较分析

文献[6]中提出的基于LT码的方法是与本文方法相关且最具代表性的一种方法。本节中通过实验比较和分析了2种方法的源数据包传递性能和源数据包恢复性能。表3~5所列为2种方法的数值实验结果。

表3所列为在源数据包传递性能实验中，在保证每个源数据包都能访问网络中的所有节点的前提下，平均每个源数据包在网络中的传递次数对比。

从表3可知：采用本方法每个源数包在网络中的传递次数是文献[6]中方法的37% ~ 45%，平均值约为39%。在实际应用中传递源数据包意味着网络中节点通信能量的消耗，因此与文献[6]中方法相比，本文方法可在实际应用中节约55% ~ 63%的通信能耗(平均值约为61%)。

表4与表5所列为2种方法的源数据包恢复性能对比实验数值。由于文献[6]的方法是基于LT码的，因此Sink节点为了恢复出k个源数据包而需要访问的存储数据包的个数，与LT码的译码性能有关，无论是LT码的译码性能理论分析^[13]还是文献[6]的实验都表明，当k为几百时，只有当源数据包恢复开销η接近k的值时，Sink节点的才能成功恢复出源数据包。表4和表5所列实验数值验证了这一结论。

从表4可以看出：采用文献[6]中方法，Sink节点需要访问约200个存储数据包才能以100%的概率恢复出原来的100个源数据包。而采用本文方法，Sink节点访问了110个存储数包后，就能以100%的概率恢复出原来的100个源数据包，访问成本节约了45%。 同样地，从表5可以看出：采用文献[6]中方法，Sink节点需要访问520个存储数据包才能以100%的概率恢复出原来的300个源数据包。而采用本文方法，Sink节点访问了310个存储数包后，就能以100%的概率恢复出原来的300个源数据包，访问成本节约了40%。

表3  平均每个源数据包传递次数对比(源数据包对网络覆盖率为100%)

Table 3  Average transmitting times of every source data packet in network on condition that every source data packet covers whole network

表4  源数据包恢复性能对比(n=300, k=100, a=2)

Table 4  Comparison of source data packet recovery performance for n=300, k=100, a=2

表5  源数据包恢复性能对比(n=900, k=300, a=2)

Table 5  Comparison of source data packet recovery performance for n=900, k=300, a=2

综上所述可以得出结论：采用本方法可以有效节约存储过程中的通信成本和Sink节点的访问成本。

4  结论

(1) 依靠源数据包传递过程中的定向随机游走机制和网络每个节点对源数据包的独立计算产生机制，提出了一种简单高效的分布式的数据存储算法。

(2) 与同类方法相比，本方法有效降低了存储过程中各传感器节点的通信能耗和Sink节点的访问成本。

(3) 本算法对k个源数据包是做为一个整体来存储的，存储完成之后，Sink节点在访问过程中只能一次性地恢复出k个源数据包。在未来的研究工作中，将考虑如何针对用户需要单独地存储和读取某个特定源数据包。

参考文献：

[1] 蔚赵春, 周水庚, 关佶红. 无线传感器网络中数据存储与访问研究进展[J]. 电子学报, 2008, 36(10): 2001-2010.

YU Zhaochun, ZHOU Shuigeng, GUAN Jihong. Data storage and access in wireless sensor networks: A survey[J]. Acta Electronica Sinica, 2008, 36(10): 2001-2010.

[2] Vitali D, Spognardi A, Villani A, et al. Replication schemes in unattended wireless sensor networks[C]//Proceedings of 2011 4th IFIP International Conference on New Technologies, Mobility and Security. Paris: IFIP, 2011: 1-5.

[3] 任伟, 任毅, 张慧, 等. 无人值守无线传感器网络中一种安全高效的数据存活策略[J]. 计算机研究与发展, 2009, 46(12): 2093-2100.

REN Wei, REN Yi, ZHANG Hui, et al. A secure and efficient data survival strategy in unattended wireless sensor networks[J]. Journal of Computer Research and Development, 2009, 46(12): 2093-2100.

[4] Madsen T K, Grauballe A, Jensen M G, et al. Reliable cooperative information storage in wireless sensor networks[C]//Proceedings of the IEEE International Conference on Telecommunications. Petersburg: IEEE, 2008: 1-6.

[5] Aly S A, Kong Z, Soljanin E. Raptor codes based distributed storage algorithms for wireless sensor networks[C]//Proceedings of the IEEE International Symposium on Information Theory. Toronto: IEEE, 2008: 2051-2055.

[6] Kong Z, Aly S A, Soljanin E. Decentralized coding algorithms for distributed storage in wireless sensor networks[J]. IEEE Journal on Selected Areas in Communications, 2010, 28(2): 261-267.

[7] Jamalipour J S. Distributed data storage in large-scale sensor networks based on LT codes[EB/OL]. [2012-01-21]. http://arxiv.org/ftp/arxiv/ papers/1201/1201.4479.pdf.

[8] Aly S A, Kong Z, Soljanin E. Fountain codes based distributed storage alogorithms for large-scale wireless sensor networks[C]//Proceedings of the IEEE 7th international Conference on Information Processing in Sensor Networks. Louis: IEEE, 2008: 171-182.

[9] Cooper C, Frieze A. The cover time of random geometric graphs[J]. Random Structures and Algorithms, 2011, 38(3): 324-349.

[10] Tzevelekas L, Oikonomou K, Stavrakakis I. Random walk with jumps in large-scale random geometric graphs[J]. Computer Communications, 2010, 33(13): 1505-1514.

[11] Avin C, Krishnamachari B. The power of choice in random walks: An empirical study[J]. Computer Networks, 2008, 52(1): 44-60.

[12] Avin C, Krishnamachari B. The power of choice in random walks: An empirical study[C]//Proceedings of the 9th ACM International Symposium on Modeling Analysis and Simulation of Wireless and Mobile Systems. New York: ACM, 2006: 219-228.

[13] Shokrollahi A. Raptor codes[J]. IEEE Transactions on Information Theory, 2006, 52(6): 2551-2567.

(编辑  陈爱华)

收稿日期：2013-02-23；修回日期：2013-05-05

基金项目：国家重点基础研究发展计划(“973”计划)项目(2011CB302402)；国家高技术研究发展计划(“863”计划)项目(2008AA01Z402)

通信作者：肖宜龙(1983-)，男，山西朔州人，博士研究生，从事信息编码及信息存储等研究；电话：15008428215；E-mail：yilongxiao@foxmail.com