覆冰导线融冰计算模型

顾小松^{1, 2}，王汉青¹，刘和云³

(1. 中南大学 能源科学与工程学院，湖南 长沙，410083；

2. 长沙理工大学 能源与动力工程学院，湖南 长沙，410007；

3. 湖南人文科技学院 计算机科学系，湖南 娄底，410007)

摘  要：以覆冰导线为研究对象，根据热平衡方程，建立焦耳热融冰的数学模型。介绍导线覆冰的基本理论，以冰筒直径、冰平均密度以及冰表面平均温度作为融冰模型的输入，提出融冰临界电流这一决定融冰能否进行的指标。用Visual Basic和Visual Fortran混合编程编写计算融冰时间的可视化程序，输入相关气象参数、结冰时间、电阻以及电流即可计算融冰时间。把程序计算结果与加拿大魁北克大学冰风洞中实验结果进行对比，结果表明：计算值与实验值的最大相对误差不超过10%，验证了模型的正确性；该模型可用于导线融冰装置融冰时间和电流的计算。

关键词：导线；融冰；覆冰；临界电流；风洞

中图分类号：TM75          文献标志码：A         文章编号：1672-7207(2010)05-2011-06

Calculation model of ice melt on wires with ice accretion

GU Xiao-song^{1, 2}, WANG Han-qing¹, LIU He-yun³

(1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;

2. School of Energy and Power, Changsha University of Science and Technology, Changsha 410083, China;

3. Department of Computer Science and Technology, Hunan University of Humanities,
Science and Technology, Loudi 417000, China)

Abstract: Taking ice covered wires as a research object, a mathematical model was established based on the heat balance equation, and the theory of ice accretion on wires that provided ice sleeve diameter, average ice density and average ice surface temperature was introduced. Mixed programming method with Visual Basic and Visual Fortran languages was used to write visual computational program to get ice melting time by inputting relative atmospheric parameters, icing duration, electric resistance and current intensity. A method taking critical electric current as a index to decide whether ice melting process happens or not was presented, and comparison of the experimental results of icing wind tunnel test in University of Quebec with computing results was made. The result shows that the maximum error is lower than 10%, the model is validated and can provide ice melting time and current intensity for ice melting equipment.

Key words: wires; ice melt; ice accretion; critical current; wind tunnel

2008-01-12—2008-02-04，我国华南、西南、华中和华东地区先后遭受低温雨雪冰冻气候袭击。这次冰雪灾害天气持续时间长，影响范围广，危害程度大，全国有20个省(自治区、市)受到不同程度的影响。几十年来，国内外一直在探讨输电线路覆冰形成机理以及防止导线覆冰的技术措施，提出了上百种防冰、融冰方法，在一定程度上减少了冰灾事故发生概率。国外关于导线覆冰的研究起步早，1981—1984年Makkonen建立了结冰圆柱体的热平衡方程，提出了架空导线结冰的计算模型^[1-3]。随着覆冰理论的完善以及冰风洞实验技术的发展，改进的覆冰模型^[4]成功应用于各种大气构件结冰的模拟。刘和云等^[5-6]对国内外的覆冰模型进行了比较，指出了它们的优缺点以及适用范围。Personne等^[7-11]较全面地介绍了导线防冰、融冰理论及其工程应用；Zsolt^[12]提出了导线融冰的2种模型，并在加拿大魁北克大学冰风洞中做了相应的实验,但模型只是针对某一冰筒直径以及假定的冰密度来计算融冰焦耳热，并没有考虑实际的覆冰情况和冰的平均表面温度。Maurice等^[13-14]虽然提出了同时考虑覆冰与融冰的组合模型，但没有考虑气象参数对融冰焦耳热的影响,而事实上某些气象参数对融冰焦耳热的影响较大。本文作者根据导线覆冰及融冰的热平衡方程，建立融冰电流及融冰时间计算模型，此模型综合考虑了覆冰以及各种气象参数对融冰过程的影响。利用混合语言编程技术编写了融冰计算可视化程序，并将计算结果与冰风洞中的实测值进行对比，证明程序的结果是可靠的。此程序可用于工程上架空导线、电气化铁路接触线融冰的计算，输入融冰电流，即可计算相应的融冰时间。

1  基于覆冰的导线融冰模型

1.1  导线融冰过程传热分析

覆冰在导线上的融化过程可以划分为2个阶

段^[6]；冰筒和导线紧密接触，此时融冰速率最高，然后，导线表面出现一层薄液膜，冰与导线在上部被液膜隔离。在下部为水气空间所分离，融冰速率降低。图1(a)所示是融冰的第1阶段示意图，因为导线上部一直与冰全面接触，所以，融冰率较高；图1(b)所示是融冰的第2阶段示意图，只有少量冰表面与导线接触，且随着时间的推移其接触面积越来越小，故融冰速率较低。只要通电导线将冰筒融破，随着冰面与导线接触面积的不断减小，过一段时间后，挂在导线上的残冰就会在风力和重力的作用下脱离。

为对覆冰导线的融冰过程进行传热分析，进行如下假设：(1) 导线的通过电流是发热均匀的，且在融冰过程中导线电阻恒定；(2) 不考虑冰和水的分界面位置且认为其界面温度为0 ℃；(3) 只有导线上部覆冰被融化；(4) 忽略导线上冰筒水层的影响；(5) 在融冰分析时，把导线融冰过程看成准平衡过程。

冰筒的准热平衡方程表达式为：

  (1)

式中：q_J=I²R，为单位长度导线产生的焦耳热；I为融冰电流(A)；R为单位长度导线的电阻(?/m)；?t为融冰时间；q_c为冰筒外表面与周围空气对流换热量；Q_MELT为融化覆冰所需的热量；ρ为冰筒的平均密度(kg/m³)；l为冰的融化潜热(J/kg)；c_p为冰的比定压热容(J/(kg·℃))；t₀为冰融化温度(℃)；t_s为冰筒的表面平均温度(℃)；V_MELT为融冰体积(m³)。

根据传热学中圆柱体导热的相关知识^[15]，q_c由下式求得：

             (2)

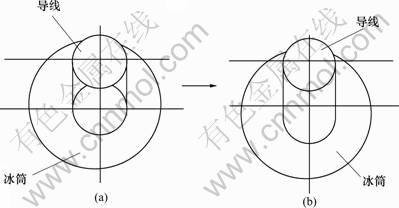
(a) 第1阶段；(b) 第2阶段

图1  导线融冰两阶段示意图

Fig.1  Schematic diagram of two stage ice melts on wires

式中：t_a为大气温度；r_i为导线覆冰圆柱的半径；r_c为导线的半径；h为大气气流横掠结冰导线的对流换热系数，它的值与冰筒的直径、表面粗糙度以及风速有关，其准则关联式为Nu=0.032Re^0.85，详见文献[2]；k_i为冰的导热系数。

融冰体积V_MELT表达式^[6]为：

V_MELT=D_idx                 (3)

式中：D_i为i时刻的冰筒的直径；dx为导线上覆冰的厚度。将q_J和q_c代入式(1)可得：

(4)

当时，方程的左边为0，

此时，计算出的电流为临界电流。临界电流是通电导线能否融冰的重要指标，若导线通电电流小于临界电流，则其产生的焦耳热全都会散失到大气中并不会被冰筒吸收，因此是不可能融冰的。临界电流由导线电阻、大气温度、对流换热系数、导线直径和冰筒直径以及冰的导热系数k_i所决定。只有当电流＞时，覆冰才开始融化。

通过以上分析要获得某一融冰电流下的融冰时间还有3个未知数：冰筒直径D_i，冰平均密度ρ，冰筒表面的平均温度。这3个量都与导线的覆冰过程有关。

1.2  导线覆冰计算

1.2.1  冰筒表面平均温度的计算

导线覆冰表面的热平衡方程为^[2]：

q_f+q_v+q_a=q_c+q_e+q_l+q_s              (5)

式中：q_f为冻结时释放的热流密度；q_v为表面气动加热热流密度；q_a为将冰从0 ℃冷却到覆冰表面温度放热热流密度；q_c为覆冰表面与空气的对流换热热流密度；q_e为覆冰表面蒸发或升华带走的热流密度；q_l为加热水滴使之温度升高到0 ℃时的热流密度；q_s为冰面辐射产生的热流密度(被忽略)。

对单位导线表面积而言，各项热流量的计算如下：

q_f=IL_f                   (6)

q_v=hrv²/(2c_p)                (7)

q_a=Ic_i(0-t_s)                 (8)

q_c=h(t_s-t_a)                 (9)

            (10)

          (11)

式中：L_f(J/kg)为水凝固释放出的潜热；I为结冰强度；h为对流换热系数；r为恢复系数(导线为圆柱时，r=0.79)；v为风速(m/s)；c_p为空气的比热容(J/(kg·℃))；c_i为冰的比热容；t_s为冰表面平均温度(℃)；t_a为空气温度；k=0.62；L_e为在t_s时蒸发或升华的潜热；p_s和p_a分别为温度在t_s和t_a时冰筒表面的饱和水蒸气压力；p=1.10×10⁵ Pa；E是收集系数，它表示实际的表面撞击水量与最大可能(整个迎风面)收集水量的比值；v是风速；w是空气中的液态水含量；c_w为水的比定压热容(J/(kg·℃))。

将式(6)~(11)代入式(5)可得到只含有冰筒平均表面温度1个未知数的方程：

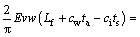
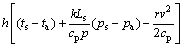       (12)

方程(12)中p_s为t_s的指数函数，因此，无法求得t_s的解析值，需要利用数值方法对t_s进行计算。将上式整理成f(t)=0的形式，此方程的根即为所求的t_s。采用二分法进行求解，基本思路是先指定1个包含零点的区间[-40, 20]，将区间逐次收缩一半，使区间的2个端点逐步逼近函数的零点。

1.2.2  冰筒直径的计算

迎风面单位表面积冰的增长速度称为结冰强度(kg/(m²?h))，其计算式^[2]为：

              (13)

其中：n为冻结系数，表示导线收集到的水冻结成冰的比例。当n＜1时，冰为湿增长，也就是说，总体上有部分水从冰筒表面流失；当n=1时，所有的水都冻结；n 的计算见文献[2]。

i时刻单位长度导线冰负荷M_i与i-1时刻的冰负荷M_i-1关系如下：

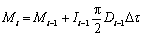          (14)

由(14)式求得冰负荷后，即可求出冰筒直径D_i：

        (15)

式中：可由Macklin公式^[2]求得。

2  融冰可视化程序编写

2.1  融冰计算模块

融冰计算流程图如图2所示。输入相关参数后，开始进行覆冰计算，输出值为冰筒与大气对流换热系数、冰筒直径、冰平均密度以及冰表面的平均温度。这些值作为融冰计算的输入，即可通过式(4)计算融冰电流和时间。

利用 Visual Fortran程序编写动态链接库(DLL)。首先，需要新建一个工程，在文件里选择Fortran Free Format Source File，在工程里选择动态链接库Fortran Dynamic Link Library。代码以子程序的形式编写，通过编译链接就得到icemelting.dll这个动态链接库   文件。

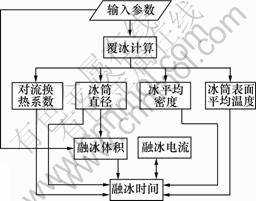
图2  融冰计算流程图

Fig.2  Flow chart of ice melting calculation

2.2  输入输出界面

程序输入输出界面如图3所示。程序的输入参数包括：大气温度、风速、液态水含量、过冷水滴直径、导线直径、大气压力、导线电阻、结冰时间和融冰电流。在输出方面，设置2个选项：一个是将计算结果保存为Excel表格，一个将计算结果显示在对话框中(图 4)。最后，设置1个退出按钮退出程序，结束计算。输入输出界面用Visual Basic编写，通过调用融冰计算动态链接库(icemelting.dll)完成融冰计算。按照理论模型，当融冰电流小于临界电流时，融冰时间为负值，表明融冰过程不可能进行，因此，在程序中设定若融冰时间为负值，则令其为0。

图3  程序输入输出界面

Fig.3  Program input and output interface

图4  程序计算结果分析界面

Fig.4  Program interface of computational results

3  计算程序的验证

3.1  CIGELE冰风洞

加拿大魁北克大学的CIGELE冰风洞是为对大气构件结冰进行实验研究而专门建造的。其循环方式为闭式循环，总长度约30 m，如图5所示，它包括回流段、动力段、制冷机、回流段和试验段。通过调节制冷机的冷量来改变空气温度，最低温度可以达到-40 ℃。通过改变风机变频器的频率来调整风速，风速可在0~29 m/s间调节。通过改变连接喷嘴的气源及水源压力和流量，就能调节风洞中过冷水滴粒径及液态水含量。测试段由透明有机玻璃做成，内设有各种传感器及数据采集系统，待测试的构件(例如导线)放置在垂直于来流的方向上。

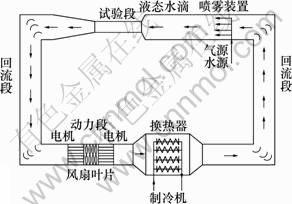
图5  冰风洞示意图

Fig.5  Schematic diagram of icing wind tunnel

3.2  计算值与实验数据比较

Zsolt^[12]在CIGELE的冰风洞中进行的融冰实验结果如表1所示，相应实验条件下的计算值如表2所示。相关参数为：导线直径D_C=30.48 mm，大气压力p=0.09 MPa，单位长度的导线电阻R=0.052 ?/km，覆冰时间为0.6 h。

表1  冰风洞中融冰实验数据

Table 1  Test results of ice melt in icing wind tunnel

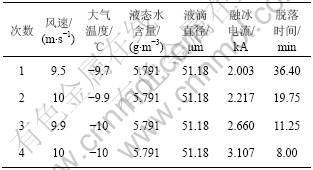
表2  冰筒融冰计算数据

Table 2  Calculation results of ice melt on ice sleeve

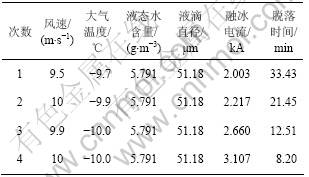
图6所示为实验及计算融冰时间与电流的关系。可见：当融冰电流为2.217 kA时，两者误差最大，为8.6%。融冰电流为3.107 kA时，两者误差最小，为2.5%。从图6还可以看出：计算融冰时间普遍比实验融冰时间长。其原因主要是模型中融冰体积比实际融化的体积大以及覆冰计算出的冰密度比实际值大。融冰电流和融冰时间实验值和计算值的误差在合理的范围内，证明本文提出的融冰模型是合理的。

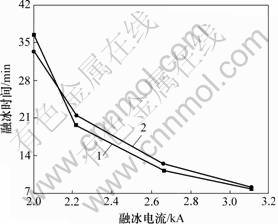
1—实验融冰时间；2—计算融冰时间

图6  实验及计算融冰时间与电流的关系

Fig.6  Relationship between ice melting time and electric current

4  结论

(1) 冰风洞实验证明了本文提出的基于覆冰的导线融冰计算模型是合理的，编写的融冰计算程序可为架空导线、电气化铁路接触线上的融冰装置提供所需融冰时间下的融冰电流。

(2) 输入导线融冰的电流一定要大于其临界电流，否则不但不能融化覆冰，而且会使覆冰加剧，因此，临界电流是判断导线融冰能否进行的重要指   标。融冰电流与气象参数、导线类型以及冰的导热系数有关。

参考文献：

[1] Makkonen L. Estimating intensity of atmospheric ice accretion on stationary structures[J]. Journal of Applied Meteorology, 1981, 20(2): 595-600.

[2] Makkonen L. Modeling of ice accretion on wires[J]. Journal of Climate and Applied Meteorology, 1984, 23(1): 29-39.

[3] Makkonen L. Heat transfer and icing of a rough cylinder[J]. Cold Regions Science and Technology, 1985, 10(2): 105-116.

[4] Makkonen L. Models for the growth of rime, glaze, icicles and wet snow on structures[J]. The Royal Society, 2000, 358(4): 2913-2939.

[5] 刘和云, 周迪, 付俊萍, 等. 导线雨淞覆冰预测简单模型的研究[J]. 中国电机工程学报, 2001, 21(4): 44-47.
LIU He-yun, ZHOU Di, FU Jun-ping, et al. A simple model for predicting glaze loads on wires[J]. Proceedings of the CSEE, 2001, 21(4): 44-47.

[6] 刘和云. 架空导线覆冰防冰的理论与应用[M]. 北京: 中国铁道出版社, 2001: 123-125.
LIU He-yun. Theory and application of ice accretion and de-icing on overhead lines[M]. Beijing: China Railway Press, 2001: 123-125.

[7] Personne P, Gayet J F. Ice accretion on wires and anti-icing induced by joule effect[J]. Journal of Applied Meteorology, 1988, 27(2): 101-114.

[8] Poots G. Ice and snow accretion on structures[M]. England: Research Studies Press, 1996: 96-104.

[9] Laforte J L, Allaire M A, Laflamme J. State-of-the-art on power line de-icing[J]. Atmospheric Research, 1998, 46(3): 143-158.

[10] Chii D, Yeh M. Cool thermal discharge from ice melting with heat fluxes on the boundary[J]. Energy, 1996, 2(1): 455-461.

[11] Zsolt P, Masoud F. Assessment of the current intensity for preventing ice accretion on overhead conductors[J]. IEEE Transactions on Power Delivery, 2007, 22(1): 565-574.

[12] Zsolt P. Modeling and simulation of the icing process on a current-carrying conductor[D]. Universite Du Quebec, 2006: 125-131.

[13] Maurice H, Christian L, Josee C. Combined models for glaze ice accretion and de-icing of current-carrying electrical conductors[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1611-1616.

[14] Huneault M, Langheit C, Benny J, et al. A dynamic programming methodology to develop de-icing strategies during ice storms by channeling load currents in transmission networks[J]. IEEE Transaction on Power Delivery, 2005, 20(2): 1604-1610.

[15] 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 2006: 41-55.
YANG Shi-ming, TAO Wen-quan. Heat transfer[M]. Beijing: High Education Press, 2006: 41-55.

(编辑 刘华森)

收稿日期：2010-01-03；修回日期：2010-04-15

基金项目：国家自然科学基金资助项目(50676030；50976030)；湖南省科技厅计划项目(2007FJ4137)

通信作者：顾小松(1978-)，男，湖北京山人，博士研究生，讲师，从事导线覆冰及融冰数值模拟、结冰风洞实验研究；电话：0731-82618565；E-mail:gu_xiao_song@163.com