文章编号：1004-0609(2008)12-2224-09

金属Mg晶格稳定性的第一原理电子结构计算

陶辉锦^{1, 2}，尹  健³，尹志民¹，张传福²，李  劼²，黄伯云³

(1. 中南大学 材料科学与工程学院，长沙 410083；

2. 中南大学 冶金科学与工程学院，长沙 410083；

3. 中南大学 粉末冶金国家重点实验室，长沙 410083)

摘  要：采用最小二乘法对SGTE纯单质数据库中金属Mg的Gibbs能表达式进行了重新评估，得到了比SGTE数据库更精确的结果；同时，将SGTE数据库的晶格稳定参数外推至0 K，与第一原理总能赝势平面波方法的结果进行了对比，发现第一原理的晶格稳定参数结果为?G^bcc?hcp＞?G^fcc?hcp＞0，与SGTE外推结果一致。同时，研究还发现：第一原理总能平面波赝势方法计算的hcp-、fcc-和bcc-Mg的晶格常数和原子体积比实验值以及投影缀加波方法得到的结果偏大，结合能出现了完全相反的结果, 并且3种结构的部分s态电子转化为p态电子形成了更强的化学键。

关键词：Mg；Gibbs能；电子结构；晶格稳定性；第一原理

中图分类号：TG 111       文献标识码： A

Calculations of lattice stabilities of elemental Mg from electronic structures in first principles

TAO Hui-jin^{1, 2}, YIN Jian³, YIN Zhi-min¹, ZHANG Chuang-fu², LI Jie², HUANG Bo-yun³

(1 School of Materials Science and Engineering, Changsha 410083, China;

2. School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China;

3. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China)

Abstract: The correction of transition data and reassessment of the parameters of Gibbs energy of elemental Mg were performed with the least-square method and the results agree more accurately with JANAF data than those of SGTE database. At the same time, the lattice stability parameters obtained by CALPHAD method in SGTE database were extrapolated to 0 K, and these results were compared with those of total energy plane wave pseudopotential method in first principles. It is found that the result of first principles agrees completely with that of SGTE, ?G^bcc?hcp＞?G^fcc?hcp＞0. Besides, it is found that the results of lattice constants and atomic volumes of hcp-, fcc- and bcc-Mg calculated by total energy plane wave pseudopotential method are much larger than experimental data and those of projector augmented wave method in first principles. The contrary case occurs in total energy. And part of s state electrons in atoms were changed into p state electrons in crystals to form stronger chemical bonding.

Key words: Mg; Gibbs energy; electronic structure; lattice stability; first principles

相图的计算模拟(CALPHAD，CALculations of PHAse Diagrams)一直被认为是指导新材料开发设计的强有力工具^[1?2]，对纯单质不同晶体结构相对Gibbs能，即晶格稳定参数的评估是CALPHAD的重要基础。其中，SGTE(Scientific Group Thermodata Europe) 纯单质数据库^[3]已经给出298.15 K以上78种元素的晶格稳定参数和不同晶体结构的Gibbs能表达式。与建立在对实验数据拟合并进行外推基础上的CALPHAD方法互为补充的是，第一原理方法在不依赖实验资料的情况下可以进行纯单质不同晶体结构的总能、晶格常数和态密度等物理性质的理论计算，更好地理解纯单质晶格稳定性的物理原因^[4?13]。

由于SGTE数据库中用于金属Mg Gibbs能评估的JANAF (Joint Army Navy Air Force)数据库已经得到更新，本文作者将首先采用最新的JANAF数据(第四版)^[14]，运用最小二乘法重新评估Mg的Gibbs能表达式；其次，将SGTE 数据库中CALPHAD方法得到的Mg的晶格稳定参数^[15]外推至0 K，同时采用第一原理总能平面波赝势方法^[16?22]计算hcp-、fcc-和bcc-Mg 0 K的总能、晶格常数和态密度等物理性质；最后，将CALPHAD方法、第一原理总能平面波赝势方法和第一原理投影缀加波方法^[23?24]的结果进行对比分析，找到CALPHAD方法与第一原理方法的差异，探索金属Mg晶格稳定性的物理原因，同时为Mg合金的相图计算及成分设计提供基础数据。

1  原理与方法

1.1  最小二乘原理

由于不可能要求近似的拟合曲线y=f(x)严格地通过所有的实验数据点(x_i, y_i),即不可能要求理论函数在x_i的偏差δ_i=f(x_i)?y_i都严格地等于零，所以，为了使理论曲线能尽量地反映所给数据的变化趋势，要求│δ_i│或│δ_i│²尽量小，为了计算、分析与应用的方便，一般根据“偏差平方和最小”的原则(称为最小二乘法)来选取拟合曲线,即由待定系数a_i=(i=0, 1, ???, n)确定的理论函数Y=f(x, a₀, ???, a_n)使得偏差平方和函数

当加权系数w_i不全取1时，称为加权最小二乘拟合；当F为a_i的非线性函数时称为非线性最小二乘拟合；当F为a_i的线性函数时则称为线性最小二乘拟合^[25]。本研究采用线性最小二乘拟合，且加权系数w_i全取1。

在具体寻找拟合曲线y=f(x)，即Y=f(x, a₀, ???, a_n)时，一般会采用某个函数类φ={φ₀(x), φ₁(x), ???, φ_n(x)}，如x的0，1，???, n次方等相互正交的函数构成的函数类，以构建理论函数，即

本研究采用完全主元高斯消去法实现对上述矩阵的求解^[26]。

1.2  Gibbs能评估原理与方法

在确定热力学函数表达式之前，根据JANAF^[14]数据对元素Mg的转变数据进行了修正，结果如表1所列。

1.2.1  恒压热容Cp

在SGTE纯单质数据库中，恒压热容，焓，熵和Gibbs能的分别采用如下表达形式^[3]：

本研究仍然采用SGTE数据库的函数形式来进行最小二乘拟合，以确定固相摩尔突压热容表达式(10)中的参数c和d，对于Liquid相则只需确定参数c。

1.2.2  焓H

由于SGTE纯单质数据库中的能量表达式是以298.15 K和10⁵ Pa条件下稳定状态的元素焓值H_SER

为参考态的，对金属Mg而言，H_SER=，因此，

根据这一条件可以确定Mg 的hcp相Gibbs能表达式参数a；根据hcp相的a、c和d值，Liquid相的c，以及表1中熔点温度时的转变焓值Δ_transH，可以确定Liquid相焓值表达式(11)中的参数a。

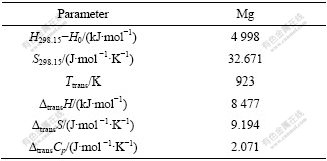
表1  金属Mg的转变数据

Table 1  Transition data of elemental Mg

1.2.3  熵S

类似的，根据表1中的S_{298.15 K}，由表达式(12)有

从而可以确定hcp-Mg熵值表达式(12)中的参数b；进而根据hcp固相的b、c和d值，Liquid相的c值，以及表1中熔点温度时的转变熵值Δ_transS，可以确定Liquid相熵值表达式(12)中的参数b。

1.2.4  非自然态参数的确定

根据已经确定的自然态hcp-Mg Gibbs能表达式中的参数a, b, c和d，采用SGTE数据库中对过热固相添加T^?9项和对过冷液相添加T⁷项的CALPHAD处理方法，并且保持分段函数在转变点焓值和熵值的连续性，可以确定从298.15 K至沸点固相和Liquid液相的表达式，然后，引用Saunders的晶格稳定参数^[15]可以对fcc和bcc亚稳相Gibbs能表达式中的参数加以确定。

1.3  第一原理方法

1.3.1  第一原理

对材料进行微观描述的基础是多粒子薛定谔方程

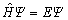                                (17)

原则上说，N 体波函数包含了所有可能的信息，通过严格求解薛定谔方程，可以得到体系的所有物理量。虽然原则上可以通过量子力学对该体系进行求解，但由于材料这一物质系统过于复杂，必须采取合理的简化和近似才能有效地进行计算。作为初步近似，引进以下3个假设将问题简化：

1) 非相对论近似，即求解非相对论的薛定谔方程，而不是相对论的狄拉克方程；

2) 波恩?奥本海默近似，即假定电子和核的运动是相对独立的，这样就可以把体系的薛定谔方程分解为描述核运动的方程与描述电子运动的方程；

3) 单电子近似，即把体系中电子的运动看成是每个电子在其余电子的平均势场作用下运动，从而把多电子的薛定谔方程简化为形式上的单电子方程。

基于上述3个假定(主要是后两个假定)的求解电子薛定谔方程的方法被称为从头算方法(Ab intio)，一般为了与从头算的其它方法相区分，通常把基于密度泛函理论的从头算称为第一原理，其理论基础—密度泛函理论是完全基于量子力学的从头算理论。

1.3.2  密度泛函理论

HOHENBERG和KOHN^[27]于1964年证明了体系基态的电子密度分布完全决定体系的性质，从而奠定了密度泛函理论(Density-functional theory, DFT)的基础。KOHN和SHAM^[28]于1965年进一步提出了Kohn-Sham方程：

Kohn-Sham方程的建立标志着第一原理密度泛函理论的完全建立，该密度泛函理论用粒子数密度而不是波函数来描述体系，用它来描述体系显然比波函数描述简单得多，特别是在处理大体系时，问题可以得到极大的简化。

1.3.3  LDA和GGA近似

Kohn-Sham方程原则上是精确的，只要知道精确的能量密度泛函形式，就可由该方程求出密度分布函数，进而得到体系的性质。然而，完全精确的能量密度泛函无法获知，只能使用近似方法，常用的近似能量密度泛函有局域密度近似^[29](Local Density Approximation, LDA)和广义梯度近似^[30](Generalized Gradient Approximation, GGA)。其中，局域密度近似(LDA)的基本想法在于利用均匀电子气的密度函数ρ(r)得到非均匀电子气的交换-关联泛函，在该框架下可以给出E_XC[ρ(r)]的具体形式，并可通过求解一组单粒子在有效势场中运动的方程而得到电子密度的分布，进而在此基础上计算固体的有关特性。在广义梯度近似(GGA)中，交换关联势不仅与局域密度有关，还与密度函数的一阶和二阶导数(梯度)有关，因而在某些情形下改善了局域密度近似的计算结果。

1.3.4  平面波赝势方法

从数学上讲，任何一个数学完备集都可以作为Kohn-Sham方程的初始解，但如果要保证求解迭代过程不发散且能迅速收敛则需要精心构造基函数，不同的基函数在解Kohn-Sham方程时有着不同的优点和缺点。基于密度泛函理论的常用方法是平面波赝势法，其它还有全势线性Muffintin轨道^[31](Full Potential Linear Muffin-tin Orbital, FPLMTO)及全势线性缀加平面波^[32](Full Potential Linear Augmented Plane Wave, FPLAPW)等方法，这些方法在计算中几乎不用任何经验参数，并且有着坚实的物理理论基础，只要在计算中设置足够高的精度就可得到可信度很高的计算结 果^[33]。

1.4  计算方法和主要参数

本研究计算采用的是基于密度泛涵理论(DFT)的第一性原理总能平面波赝势方法, 所有的计算都在CASTEP程序完成。晶格常数和总能计算均使用GGA 近似和超软赝势^[34]。在每一原胞体积下，先进行中等精度的几何优化，再进行高精度优化，最后进行超高精度优化，然后单独计算总能和其它物理性质，以避免Pulay应力^[35]的影响。hcp-、fcc-和bcc-Mg k空间积分网格点分别为9×9×6、10×10×10和10×10×10，平面波动能截断能量为380 eV。同时，为了加速布里渊区积分的收敛，采用有限温度Smearing方法^[36]，几何优化时采用Gaussian Smearing方法^[37]，Smearing宽度为0.1 eV。

2  计算结果

2.1  热力学性质

2.1.1  Gibbs能评估结果

根据上述原理和方法，对SGTE纯单质数据库中金属Mg的Gibbs能表达式参数进行了修正后得到了表2的结果，其单位为J/mol。

表2  对SGTE纯单质数据库中金属Mg的Gibbs 能进行重新评估后的结果

Table 2  Reassessed functions of Gibbs energy of SGTE database of elemental Mg

2.1.2  恒压热容C_p评估结果

将上述最小二乘法重新评估、JANAF数据和SGTE纯单质数据库得到的恒压热容C_p进行了对比，如图1所示。

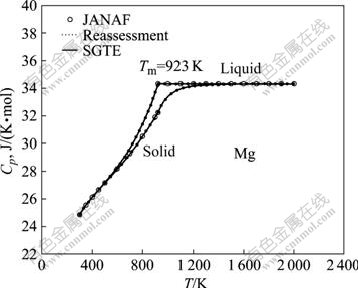
图1 由本工作重新评估和SGTE 数据库所得Mg 的恒压热容与JANAF数据的对比

Fig.1　Comparison of isobaric heat capacity of Mg metals between reassessment calculations in this work, SGTE database and JANAF data

图1表明本研究最小二乘法重新评估结果和SGTE纯单质数据库结果均与JANAF数据一致，且本文结果与SGTE数据库结果高度重合，难以区分和比较，因此，以JANAF数据为参考，表3进一步给出了二者评估结果的定量差别：

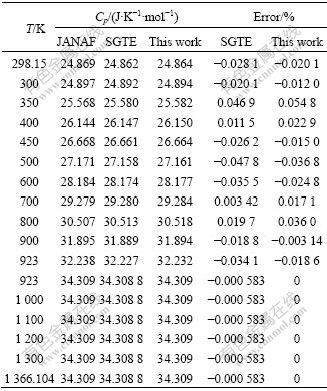
表3 本文重新评估和SGTE 数据库所得Mg 的恒压热容与JANAF数据的对比

Table 3　 Comparison of isobaric heat capacity of Mg metals between reassessment calculations in this work, SGTE database and JANAF data

2.1.3  晶格稳定参数评估结果

本研究将SGTE数据库中CALPHAD方法，即SAUNDERS等^[15]的晶格稳定参数外推至0 K，并在以下分析和讨论中与第一原理计算结果进行对比，图2所示为外推的晶格稳定参数图：

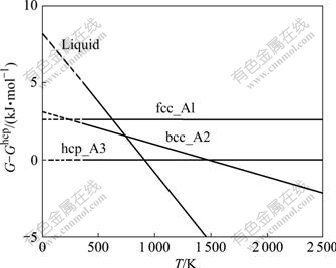
图2  由本工作外推至0 K得到的金属Mg 的晶格稳定参数

Fig.2　Lattice stability parameters extrapolated to 0 K of elemental Mg in this work

2.2  第一原理计算结果

2.2.1  晶格常数和原子体积

表4列出了优化后的晶格常数和原子体积结果。

表4  hcp-、fcc-和bcc-Mg 0 K的理论晶格常数和原子体积

Table 4　Theoretical lattice constants of hcp-, fcc- and bcc-Mg at 0 K

2.2.2  总能和结合能

总能和结合能的计算结果如表5所示，其中结合能是指将0 K和1个大气压下的固体拆成基态自由原子所需的能量^[38]。根据焓的定义 H=U+PV 知，由于固体等凝聚态体系的体积相对于同组成的气体非常微小，几乎可以忽略，因此在1个大气压下，凝聚态体系焓 H 中的PV项可以忽略，此时焓H与内能U近似相等，因此，将0 K和零压下的固体拆成基态自由原子所需的能量可以近似为结合能。同时，本文将hcp-Mg的晶格常数设置足够远(a=1 nm，c=1.633 nm)使得计算的原子间作用力为零，并且使得计算得到Mg原子的轨道电子占据数为1s²2s²2p⁶ 3s²，与原子基态的电子组态相同，此时得到的总能视为基态自由原子总能，则hcp-、fcc-和bcc-Mg的总能与该总能之差的绝对值即为结合能。表5给出了计算结果。

表5  hcp-、fcc-和bcc-Mg 0K的总能和结合能

Table 5  Total energy and cohesive energy of hcp-, fcc- and bcc-Mg at 0 K

2.2.3  态密度和轨道电子占据数

电子结构的差异是晶格稳定性差异的根本原因，因此，本研究计算并绘出了hcp-、fcc-和bcc-Mg的价层2p⁶3s²电子的总态密度(见图3(a))、s态电子分态密度(见图3(b))、p态电子分态密度(见图3(c))、hcp-Mg的分态密度(见图3(d))、fcc-Mg的分态密度(见图3(e))、 bcc-Mg的分态密度(见图3(f))。

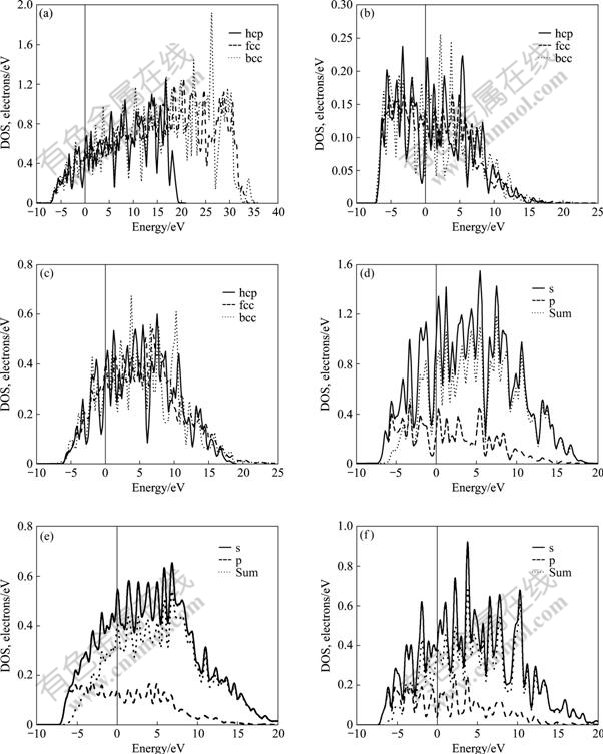
图3  hcp-、fcc-和bcc-Mg的态密度

Fig.3　Sum of partial density of state(a), partial density of s state(b), partial density of p state(c) of hcp-, fcc-, bcc-Mg and density of state of hcp-Mg(d), fcc-Mg(e), bcc- Mg(f)

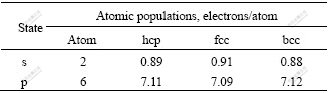
表6  hcp-、fcc-和bcc-Mg 的轨道电子占据数

Table 6  Atomic populations of hcp-, fcc- and bcc-Mg

3  分析与讨论

3.1  Gibbs能与晶格稳定参数

表3的数据对比表明：重新评估的结果在熔点923 K以前的11个温度点中有7个点的数据比SGTE更精确，熔点以后的6个温度点均比SGTE精确，评估结果总体上比SGTE结果更接近JANAF数据，因而更精确。

晶格稳定参数实质上是相对Gibbs能，描述的是相与相之间的相对稳定性，对金属Mg而言，为fcc-和bcc-Mg相对hcp-Mg的Gibbs能差(G?G^hcp)随温度变化的关系。由于本研究仅讨论0 K的晶格稳定问题，此时，根据Gibbs能定义有

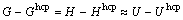               (20)

因此，可以将Saunders，即CALPHAD方法外推至0K的结果与第一原理总能平面波赝势(CASTEP)以及投影缀加波方法(VASP)的结果进行对比，并用于研究基于实验的拟合评估方法与基于纯理论的第一原理方法之间以及第一原理自身不同方法之间的差别。(G?G^hcp)的结果对比如表7所列。

表7  hcp-、fcc-和bcc-Mg 0K的晶格稳定参数

Table7  Lattice stability parameters of hcp-, fcc- and bcc-Mg at 0 K

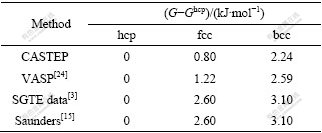
由表7可知：1) 以上第一原理方法得到的晶格稳定参数结果与CALPHAD方法一致，即4种方法均有?G^bcc?hcp＞?G^fcc?hcp＞0；2) 前两种第一原理方法的晶格稳定参数结果均比CALPHAD方法, 即SGTE和Saunders的结果偏小，且bcc结果差别相对偏小，fcc相的结果显著偏小；3) 第一原理CASTEP方法得到的fcc和bcc相的晶格稳定参数结果比VASP方法偏小；4) 表中4种方法得到的bcc相对于fcc相的Gibbs自由能?G^bcc?fcc依次为1.44、1.37、0.50和0.50 kJ/mol，前两种第一原理方法比较接近，但与CALPHAD方法结果差别较大。

3.2  晶格常数和原子体积

表8列出了金属Mg晶格常数和原子体积第一原理总能平面波赝势和投影缀加波方法以及实验值的对比结果。

表8  hcp-、fcc-和bcc-Mg 0K的晶格常数和原子体积

Table 8  Lattice constants and atomic volumes of hcp-, fcc- and bcc-Mg at 0 K

由表8可知：1) 对于hcp-Mg，第一原理总能平面波赝势方法(CASTEP)计算的晶格常数a比投影缀加波方法(VASP)和实验值都要大，但轴比c/a明显偏小；2)第一原理总能平面波赝势方法计算得到的hcp-、fcc-和bcc-Mg的原子体积总是偏大，即使hcp-Mg的轴比c/a最小，但最大的晶格常数a仍然导致其具有最大的原子体积。

3.3  总能和结合能

总能是一个很广泛的概念，结合能实质上是以自由原子为参考态的凝聚态体系总能的绝对值，为了便于比较研究，表9以自由原子为参考态来对比总能和结合能的理论计算值差异：

表9  hcp-、fcc-和bcc-Mg 0 K的总能和结合能

Table 9  Total energy and cohesive energy of hcp-, fcc- and bcc-Mg at 0 K

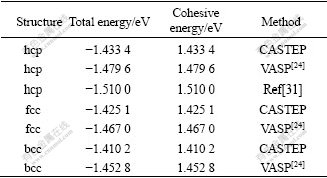
由表9可知：在本研究所设定的计算参数下，第一原理总能平面波赝势方法(CASTEP)计算的总能(结合能)绝对值比投影缀加波方法(VASP)和实验值都要小，与晶格常数和原子体积的结果相反。

3.4  态密度和轨道电子占据数

由图3(a)~(c)的总态密度，s分态密度，p分态密度的对比知：所有的s态电子已扩展分布到0至?10 eV区间，结合表6的结果知，部分s态电子已转化成p态电子，因而在图3(c)中的0至?10 eV区间出现了p态电子。

图3(d)~(f)进一步对0至?10 eV区间的态密度进行了对比。结合表6的结果可知：1) hcp-Mg(d)s态电子的态密度在该区间的积分面积(图中虚线下方面积)为0.89，fcc-Mg(e)和bcc-Mg(f)的分别为0.91和0.88，其中bcc-Mg 每个原子有1.12个s态电子转化为p态电子，转化数目最多，hcp-Mg次之，fcc-Mg最少；2) 从Fermi面所处位置看，hcp-Mg(d)处于两个密度峰的低谷中，处于明显的态密度低谷中，表现为明显的稳定相特征，fcc-Mg(e)处于峰尖，bcc-Mg(f)处于一高一低两个峰之间，结构不稳定，根据结合总能(结合能)的计算结果，bcc最不稳定，这可能与其具有最少的s态电子有关；3) 在较低能量区间，态密度DOS的顺序为DOS(s)＞DOS(p)，s态电子的态密度大，对总态密度贡献最大，较高能量区间则相反，p态电子起决定作用。

4  结论

1) 重新评估的结果更接近最新的JANAF(第四版)数据；

2) 总能赝势平面波方法得到的晶格稳定参数结果与CALPHAD方法外推结果以及第一原理投影缀加波方法的结果完全一致，即?G^bcc?hcp＞?G^fcc?hcp＞0；

3) 总能平面波赝势方法计算得到的hcp-、fcc-和bcc-Mg的晶格常数和原子体积均比投影缀加波方法大，但计算的总能绝对值(结合能)比投影缀加波方法均偏小；

4) hcp-、fcc-和bcc-Mg中所有的s态电子密度扩展分布到0至?10 eV区间，有相当一部分的s态电子已转化成p态电子，其中，bcc-Mg的转化数目最多，hcp-Mg次之，fcc-Mg最少；

5) 态密度结果表明hcp为稳定结构，fcc和bcc为不稳定结构，且总能计算结果进一步表明fcc结构比bcc更稳定，态密度图和总能算结果可以分别定性和定量分析晶格稳定性差异。

REFERENCES

[1] KAUFMAN L, BERNSTEIN H. Computer calculation of phase diagram[M]. New York: Academic Press Inc, 1970: 1?58.

[2] SAUNDERS N, MIODOWNIK A P. CALPHAD(Calculation of Phase Diagrams): A comprehensive guide[M]. New York: Pergamon, 1998: 1?66.

[3] DINSDALE A T. SGTE data for pure elements[J]. CALPHAD, 1991, 15(4): 317?425.

[4] SLUITER M H F. Ab initio lattice stabilities of some elemental complex structures[J]. Calphad-Computer Coupling of Phase Diagrams and Thermochemistry, 2006, 30(4): 357?366.

[5] CHRISTENSEN N E, NOVIKOV D L. High-pressure phases of the light alkali metals[J]. Solid State Communications, 2001, 119(8/9): 477?490.

[6] RAHMAN S M M, ALI I, BHUIYAN G M. Phase stability of alkali metals under pressure: Perturbative and non-perturbative treatments[J]. International Journal of Modern Physics B, 2002, 16(32): 4847?4864.

[7] GARCES J E, GRAD G B, GUILLERMET A F. Theoretical study of the structural properties and thermodynamic stability of the omega phase in the 4d-transition series[J]. Journal of Alloys and Compounds, 1999, 289(1/2): 1?10.

[8] GRAD G B, BLAHA P, LUITZ J. Electronic structure and chemical bonding effects upon the bcc to Omega phase transition: Ab initio study of Y, Zr, Nb, and Mo[J]. Physical Review B, 2000, 62(19): 12743?12753.

[9] GUO G Y, WANG H H. Calculated elastic constants and electronic and magnetic properties of bcc, fcc, and hcp Cr crystals and thin films[J]. Physical Review B, 2000, 62(8): 5136?5143.

[10] SIN'KO G V, SMIRNOV N A. Ab initio calculations of elastic constants and thermodynamic properties of bcc, fcc, and hcp Al crystals under pressure[J]. Journal of Physics-Condensed Matter, 2002, 14(29): 6989?7005.

[11] SKRIVER H L. Crystal structure in one-electron theory[J]. Physical Review B, 1985, 31(4): 1909?1923.

[12] 陈星秋, 李海兰, 丁学勇. 纯γ-Mn的电子、基态属性和磁有序结构[J]. 金属学报, 2002, 38(12): 1251?1256
CHEN X Q, LI H L, DING X Y. Electronic structure, ground properties and magnetic ordering for pure γ-Mn[J]. Acta Metallurgica Sinica, 2002, 38(12): 1251?1256.

[13] MISHIN Y, MEHL M J, PAPACONSTANTOPOULOS D A, VOTER A F, KRESS J D. Structural stability and lattice defects in copper: Ab initio, tight-binding and embedded-atom calculations[J]. Physical Review B, 2001, 63(22): 224106?224121.

[14] CHASE M W. NIST-JANAF Thermochemical Tables (Fourth Edition Part I) [M]. Gaithersburg: National Institute of Standards and Technology, 1998: 1005?1009.

[15] SAUNDERS N, MIODOWIK A P, DINSDALE A T. Metastable lattice stabilities for the elements[J]. Calphad-Computer Coupling of Phase Diagrams and Thermochemistry, 1988, 12(4): 351?374.

[16] SRIVASTAVA G P, WEAIRE D. The theory of the cohesive energies of solids[J]. Advances in Physics, 1987, 36(4): 463?517.

[17] BACHELET G B, HAMANN D R, SCHLUTER M. Pseudopotentials that work: From H to Pu[J]. Physical Review B, 1982. 26(8): 4199?4228.

[18] LIN J S, QTEISH A, PAYNE M C, HEINE V. Optimized and transferable nonlocal separable ab initio pseudopotentials[J]. Physical Review B, 1993, 47(8): 4174?4180.

[19] VANDERBILT D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J]. Physical Review B, 1990, 41(11): 7892?7895.

[20] MILMAN V, WINKLER B, WHITE J A, PICKARD C J, PAYNE M C, AKHMATSKAYA E V, NOBES R H. Electronic structure, properties and phase stability of inorganic crystals: A pseudopotential plane-wave study[J]. International Journal of Quantum Chemistry, 2000, 77(5): 895?910.

[21] FRANCIS G P, PAYNE M C. Finite basis set corrections to total energy pseudopotential calculations[J]. Journal of Physics: Condensed Matter, 1990, 29(19): 4395?4404.

[22] MILMAN V, LEE M H, PAYNE M C. Ground-state properties of CoSi₂ determined by a total-energy pseudopotential method[J]. Physical Review B, 1994, 49(23): 16300?16308.

[23] BL?CHL P E, JEPSEN O, ANDERSEN O K. Improved tetrahedron method for Brillouin-zone integrations[J]. Physical Review B, 1994, 49(23): 16223?16233.

[24] WANG Y, CURTAROLO S, JIANG C, ARROYAVE R, WANG T, CEDER G, CHEN L Q, LIU Z K. Ab initio lattice stability in comparison with CALPHAD lattice stability[J]. CALPHAD, 2004, 28(1): 79?90.

[25] 马振华. 现代应用数学手册?计算与数值分析卷[M]. 北京: 清华大学出版社, 2005: 15?52.
MA Zhen-hua. Handbook of modern applied mathematics: Calculations and numerical analysis[M]. Beijing: Tsinghua University Press, 2005: 15?52.

[26] 易大义, 沈云宝, 李有法. 计算方法[M]. 杭州: 浙江大学出版社, 1996: 77?86.
YI D Y, SHEN Y B, LI Y F. Calculation methods[M]. Hangzhou: Zhejiang University Press, 1996: 77?86.

[27] HOHENBERG P, KOHN W. Inhomogeneous electron gas[J]. Physical Review B, 1964, 36(3): 864?871.

[28] KOHN W, SHAM L J. Self-consistent equations including exchange and correlation effects[J]. Physical Review A, 1965, 140 (4): 1133?1138.

[29] PERDEW J P, WANG Y. Accurate and simple analytic representation of the electron gas correlation energy[J]. Physical Review B, 1992, 45(23): 13244?13249.

[30] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple[J]. Physical Review Letters, 1996, 77(18): 3865?3868.

[31] ANDERSEN O K. Linear methods in band theory[J]. Physical Review B, 1975, 12(8): 3060?3083.

[32] BLAHA P, SCHWARZ K, SORANTIN P, TRICKEY S B. Full-potential, linearized augmented plane wave programs for crystalline systems[J]. Computer Physics Communications, 1990, 59(2): 399?415.

[33] DEVANATHAN R, CORRALES L R, WEBER W J, CHARTIER A, MEIS C. Molecular dynamics simulation of defect production in collision cascades in zircon[J]. Nuclear Instruments and Methods in Physics Research, Section B: Beam Interactions with Materials and Atoms, 2005, 228(1/4): 299?303.

[34] JOHN P P, WANG Y. Accurate and simple analytic representation of the electron-gas correlation energy[J]. Physical Review B, 1992, 45(23): 13244?13249.

[35] PULAY P. Convergence acceleration of iterative sequences. the case of scf iteration[J]. Chemical Physical Letters, 1980, 73(2): 393?398.

[36] MERMIN N D. Thermal properties of the inhomogeneous electron gas[J]. Physical Review A, 1965, 137: 1441?1443.

[37] METHFESSEL M, PAXTON A T. High-precision sampling for Brillouin-zone integration in metals[J]. Physical Review B, 1989, 40(6): 3616?3621.

[38] KITTEL C. Solid state physics[M]. New York: John Wiley and Sons Inc, 1976, 55.

[39] WINTER M. Webelements[OL]. http://www.webelements.com/. The University of Sheffield and Webelements Ltd, 2006.

基金项目：教育部博士点新教师基金(20070533118), 国家自然科学基金(50471058, 50271085), 中南大学博士后基金资助

收稿日期：2008-03-06；修订日期：2008-06-24

通讯作者：陶辉锦，博士；电话：0731-8830163；Tax：0731-8876692；E-mail: thj@mail.csu.edu.cn

(编辑 何学锋)